Courses:PHYS341/2021/Project22
Physics of Acoustic Guitars
This page will describe the background, history, physics and sound proponents of the modern acoustic guitar.
Introduction/Historical Background
The acoustic guitar has its roots in ancient string instruments as seen in stone carvings from ancient Babylon 3,000 years ago. It was applied to all chordophones developed in 12th century Europe, that developed from the Greek kithara, an ancient musical instrument closely related to the lyre. In Medieval Spain, two instruments were called guitars, the Latina guitar and the Morisca guitar. They were different appearance and structure wise, but in the 14th century both were simply called guitars.

These instruments, which for the most part resemble today's acoustic guitars, did not appear until the Renaissance. In the 15th and 16th centuries, the Spaniards developed the vihuela, another stringed instrument that is similar to today's acoustic guitar. Over the years, the structure of the vihuela slowly changed and was strikingly similar to the modern acoustic guitar.
Another stringed instrument that gained popularity during this time is the baroque guitar that gained popularity in Spain, Italy and France and survived into modern times. Similar to the current acoustic guitar, but with movable frets that can be adjusted to change the tone of the instrument. It is believed that Alsl is the true predecessor of modern acoustic guitars due to its striking resemblance to the instrument. They were / are 10-string instruments like a 12-string today; usually 5 main string tones, but double strings like a 12-string guitar.
In Paris, father and son, Robert and Claude Denis created their own acoustic guitar designs, again bypassing the guitar industry. Even today, the acoustic guitar is equally popular, from concerts, performances, large orchestras to individual jam sessions and acoustic recordings.

Physical Structure of a Modern Acoustic Guitar
A guitar string has a number of frequencies at which it naturally vibrates. These natural frequencies are known as the harmonics of the guitar string. The natural frequency at which an object vibrates depends on the tension of the string, the linear density of the string, and the length of the string. Each of these natural frequencies or harmonics is assigned to a standing wave pattern. The following shows the standing wave pattern for the three lowest harmonics or frequencies of a guitar string.
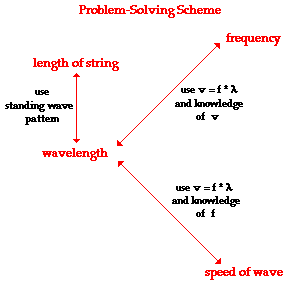
The wavelength of the standing wave for a given harmonic depends on the length of the chord (and vice versa). If the length of a guitar string is known, the wavelength associated with each of the harmonic frequencies can be found. Wavelength-wavelength relationships and the wave equation (speed = frequency * wavelength) can be combined to perform calculations that predict the length of the chord required to produce a particular natural frequency, and conversely, calculations can be performed to perform those natural frequencies produced by that known length of the guitar string. Each of these calculations requires knowledge of the speed of a wave in a string. The following diagram shows the relationships between the key variables in these calculations. These relationships are used to solve standing wave problems in musical instruments.
When an object is forced to resonate at one of its natural frequencies, it vibrates in such a way that a standing wave pattern is formed in the object. The vibrating medium vibrates in such a way that a standing wave pattern is created. Each natural frequency that an object or instrument generates has its own characteristic vibration mode or standing wave pattern. These patterns are only generated within the object or instrument at certain oscillation frequencies. These frequencies are called harmonic frequencies or simply harmonic frequencies. At any frequency other than a harmonic frequency, the resulting disturbance of the medium is irregular and does not repeat itself. In musical instruments and other objects that vibrate regularly and periodically, the harmonic frequencies are linked by simple integer ratios.
This is one of the reasons these instruments sound great. First, imagine a guitar string that vibrates at its natural or harmonic frequency. Because the ends of the string are attached and pinned to the structure of the guitars (the bridge on one end and the frets on the other), the ends of the string cannot move, so these ends become knots.There must be at least one opposing node between these two nodes at the end of the string. The most basic harmonic for a guitar string is the harmonic associated with a standing wave with only one opposing node positioned between the two nodes at the end of the string. This would be the harmonic with the longest wavelength and the lowest frequency.

The lowest frequency produced by a particular instrument is called the fundamental frequency. The fundamental frequency is also known as the instrument's first harmonic. The diagram on the right shows the first harmonic of a guitar string. If you analyze the wave pattern on the guitar string for this harmonic, you will find that there is not a full wave within the pattern. A full wave begins at the position of rest, climbs a ridge, returns to rest, falls into a valley, and finally returns to rest before the next cycle begins (Warning: The use of the words ridge and valley to describe the pattern only serves to identify the length of a repeating wave cycle.
A standing wave pattern is actually not a wave, but a wave pattern.Therefore, it does not consist of ridges and valleys, but of nodes and opposing nodes. The pattern is the result of the interference of two waves to create these knots and opposing knots.) In this pattern there is only half a wave within the length of the string. This is the case with the first harmonic or fundamental frequency of a guitar string.
Sound Measurements: Scenario
Determining Harmonic Frequencies
Imagine a guitar string 80 cm long with a fundamental frequency (1st harmonic) of 400 Hz. For the 1st harmonic, the wave length of the wave pattern would be twice as long as the string (see table above). Therefore the wavelength is 160 cm or 1.60 m. The speed of the standing wave can now be determined from the wavelength and frequency. The speed of the standing wave is:
speed = frequency • wavelength
speed = 400 Hz • 1.6 m
speed = 640 m/s
This speed of 640 m / s corresponds to the speed of a wave within the guitar string. Since the speed of a wave depends on the properties of the medium (and not on the properties of the wave), every wave has the same speed in this string, regardless of its frequency and wavelength, has the standing wave pattern, that of the second harmonic, third harmonic, fourth harmonic etc., also this speed of 640 m / s.A change in frequency or wavelength does NOT result in a change in speed.
speed = frequency • wavelength
frequency = speed/wavelength
f2 = v / λ2
f2 = (640 m/s)/(0.8 m)
f2 = 800 Hz
The same process can be repeated for the third harmonic. Using the table above, the third harmonic wavelength (denoted by the symbol λ3) would be 0.533 m (two thirds the length of the chord). The wave pattern (indicated by the symbol v) is still 640 m / s.The frequency of the third harmonic can now be determined with the wave equation (indicated by the symbol f3).
speed = frequency • wavelength
frequency = speed/wavelength
f3 = v / λ3
f3 = (640 m/s)/(0.533 m)
f3 = 1200 Hz
The following table shows that the individual frequencies in the set of natural frequencies generated by a guitar string are related by integer ratios.
Further Explanation
Sound is transmitted through a pressure wave within a material; Such a pressure wave can form when an object that is rapidly vibrating back and forth pushes air forward to break through and then moves away again, leaving a partial vacuum. When it is put under more stress, it vibrates faster, creating pressure waves that are closer together and therefore have a higher frequency. On the other hand, thicker or longer strings vibrate more slowly and create pressure waves that are further apart and therefore have a lower frequency. The volume of a sound corresponds to the amplitude of a pressure wave. The higher the pressure at the peak of the wave, the louder the sound appears to us.
The only real way to get a stronger sound from a string is to put more energy into the string, probably by playing it harder. A sound wave traveling through air is the physical length of the wave. If you could freeze a sound wave in time and space (and if you could see the wave), measuring the distance from one peak of the wave to the next would get the wavelength. An open chord, as played on a guitar, is the chord obtained by strumming a guitar that is in tune without touching the strings. A harmonic is a frequency at which a string can vibrate. The lowest frequency at which a string can vibrate is when the wavelength of the wave in the string is twice as long as the string itself.
This lower frequency is called the "fundamental frequency". The nth harmonic corresponds to a string wavelength of 1 / n times the wavelength of the fundamental wave. An overtone is very similar to a harmonic; Harmonic n is harmonic (n-1) th. One of the properties of waves, when applied to this situation, is that only integer values of n can effectively exist in a string. and forward, often along a rope or between the ends of a pipe. A node exists at the point or points where in a pipe containing a standing wave the pressure equals the ambient pressure outside the pipe.
The guitar is the most commonly used stringed instrument and shares many properties with other stringed instruments. For example, the harmonics that may be available on a stringed instrument are the same. So why does a guitar sound so different than a violin, for example?The answer lies in what harmonics are highlighted in a particular instrument based on the shape and materials in the resonator (body), the strings, the way it is played, and other factors. Attached at both ends, we will discover the harmonic row for strings that forms the basis of western harmony.

A guitar string is a common example of a double-ended string that is elastic and can vibrate. The vibrations of such a string are called standing waves and satisfy the relationship between wavelength and frequency, which results from the definition of waves: v = f, where v is the speed of the wave, f is the frequency (measured in cycles / second or Hertz, Hz) y is the wavelength. The speed v of the waves in a string depends on the tension of the
string T and the linear mass density (mass / length) µ, measured in kg / m.Waves move faster in a narrower string and therefore the frequency is higher for a given wavelength. On the other hand, waves move more slowly on a more massive string and therefore the frequency is lower for a given wavelength. The density is a little difficult to derive, but it's a simple formula: v = T / µ Since the fundamental wavelength of a standing wave on a guitar string is twice the distance between the bridge and the fret, the six strings use the same wavelength range. To have different pitches (frequencies) of the strings, you have to have different wave speeds. There are two ways of doing this: by a different voltage T or by a different mass density µ (or a combination of both).
If a tone were varied just by varying the tension, the high strings would be too tight and the low strings too loose, and it would be very difficult to play a guitar. Playing the guitar is much easier when all the strings are about the same tension. ;; Because of this, the lower strings have a higher bulk density by making them thicker and wrapping wire for the 3 bass strings. From what you've learned so far and the fact that the strings are quarter perfect in pitch. (except between the G and B strings in standard tuning) you can calculate how much µ increases between the strings so that T is constant.If a guitar string only had a single frequency vibration it would sound a little dull (you can hear a single frequency sound using the Harmonics applet).
What makes a guitar or stringed instrument interesting is the wide variety of harmonics that each wave has, satisfying the condition that there can be knots at the ends of the string in a string. The root note, the main note that you hear is the lowest note and comes from the string vibrating with a large bow.
What makes a guitar note a "guitarist" is its harmonic content and how the note rises and falls over time. It depends on how you play it, e.g. B. with a pimple in front of a finger or near the bridge or in the middle. (Of course, this does not take into account all electronic methods of emphasizing various harmonics, such as bass / treble control on electric guitars. As an example, I tested the A-string of my nylon-string guitar in two different ways: starting with the middle, the emphasizes, increases the fundamental and odd multiple harmonics that have a peak in the middle of the string and the pluck near the bridge, creating even harmonics with knots in the middle of the string to create a "buoyant" sound.
Sound Demonstration
If you gently place your finger on a speaker, you will feel it vibrate. If you play a low note out loud, you can see how it moves. As it moves forward, it compresses the air next to it and increases its pressure. Air flows outwards and compresses the next layer of air. The disturbance in the air propagates as a moving sound wave.
Ultimately, this sound wave causes a very small vibration in the eardrum, but that's another story. At any point in the air near the sound source, the molecules move back and forth, and the air pressure varies up and down in very small amounts. The number of oscillations per second is called frequency, which is measured in cycles per second or Hertz (Hz). a note is determined almost entirely by its frequency: high frequency for high pitch and low for bass.
For example, 110 cycles per second (110 Hz) is the frequency of vibration of the A string on a guitar. second fret on the G string) is 220 Hz.The next A (fifth fret on the high E string) is 440 Hz, which is the A orchestral tuning. (The A guitar string plays the A, which is usually written at the bottom of the bass clef, written an octave higher.) We can hear tones from around 15 Hz to 20 kHz (1 kHz = 1000 Hz). The lowest note on the standard guitar is E at around 83 Hz, but a bass can play as low as 41 Hz.
The original guitar can play notes with fundamental frequencies above 1 kHz. Human ears are most sensitive to sounds between 1 and 4 kHz, about two to four octaves above middle C. Although the fundamental frequency of guitar notes usually does not rise to this level. Range, the instrument emits acoustic power in this range, at the highest harmonics of most of its notes.

In order to provide defined pitch relationships between notes, metal inserts, so-called frets, are inserted into a fingerboard in the neck of the guitar. The raised edges of the frets provide fixed string lengths when the string is pressed against them with a finger. Consecutive frets are usually a semitone with the same temperament.
There are usually 19 frets on classical guitars, which can be considered an octave and a fifth with respect to the octave with the same temperament. Electric guitars can have up to 23 frets. placed by the fret rule "one eighteen of the remaining length of the string". This makes them about a semitone apart. If the musical interval produced by this rule is expressed in hertz, then a string 17/18 of its original length is an interval 98.9 hertz higher than an exact semitone of 100 hertz.
Since the barely noticeable difference in pitch is around 5 cents, the fret rule could be applied to a fret change without any problems with intonation.One would have to watch out for cumulative errors if the rule were applied repeatedly, so it should be checked at intervals like the music district, which should be exactly 3/4 the length of the open string.
Conclusion
Sound waves → higher density = higher pressure Lower density = lower pressure Different instruments playing the same note have different amounts of the same harmonic. Sound is a combination of many frequencies, it can be metal or nylon, there are special ways the string can vibrate when each part vibrates at a certain frequency in a simple harmonic motion.
The Principle of Superposition:Several waves can propagate simultaneously on the same wavelength without interfering with one another. Several waves are the sum of the displacements of individual waves. Superpositions of waves that move from left to right with the same wavelength result in standing waves. Standing wave: frequency + wavelength like waves that move.
How to determine the frequencies of the sound produced by a guitar string via vibrations they produce when the speed of the wave in the string is _____
Remember: v = y X f All frequencies are multiples of a fundamental frequency f = v / y (m / s divided by m = hz) Wave speed = m / s divided by the length of the guitar string
Important formula to find guitar frequencies / wave speed is: f = v / yv = root note f / u (for a string) y = 2l, 2l / 2, 2l / 3 (stretched string) Turn the knobs on the guitar to stretch the string more / less and to increase / decrease the tension.
Thicker string = greater mass per length.
Thin string = less mass per length
Sound is a rapid change in air pressure. We get different tones by varying the rate of change in air pressure or frequency. By vibrating a string, we can create a change in air pressure and create a sound wave. WAVES (short)
Two types exist: transversal and longitudinal transversal waves (like a guitar string), the string moves perpendicular to the movement of the wave, longitudinal waves (sound waves), the wave is a series of compressions and dilutions (decompressions) of the medium ( Air) parallel to the wave direction.
In general, the wave can be described by its speed (v), frequency (f) and wavelength.
References
“Acoustic Guitar.” Talkin Music, Talkin Music, Feb. 2015, talkinmusic.com/wp-content/uploads/2015/02/EQ-Acoustic-Guitar.jpg.
“How Does a Guitar Work?” How a Guitar Works, newt.phys.unsw.edu.au/music/guitar/guitarintro.html.
“Physics Tutorial: Guitar Strings.” The Physics Classroom, www.physicsclassroom.com/class/sound/Lesson-5/Guitar-Strings#:~:text=of 256 Hz.-,
Seering, Adam. “Guitar Building.” MIT OpenCourseWare, About MIT OpenCourseWare MIT OpenCourseWare Is an Online Publication of Materials from over 2,500 MIT Courses, Freely Sharing Knowledge with Learners and Educators around the World. Learn More " © 2001–2016 Massachusetts Institute of Technology Your Use of the MIT OpenCourseWare Site and Materials Is Subject to Our Creative Commons License and Other Terms of Use., ocw.mit.edu/high-school/engineering/guitar-building/physics-of-the-guitar/how-strings-make-sound/.
Strings, Standing Waves and Harmonics, newt.phys.unsw.edu.au/jw/strings.html.,The speed of waves in a particular guitar string,to be 405 m/s.
The Physics of Everyday Stuff - The Guitar, www.bsharp.org/physics/guitar.