Course:Phys341 2020/Example

See project guidelines, marking scheme and calendar of deadlines in course Canvas pages.

This is how to put audio files into the wiki: Upload the mp3 (no wav, but Audacity can convert wav to mp3) and go through all the copyright declarations. e.g. My daughter playing Ashokan Farewell on my balsa wood violin

Example Writing Project: The Sound Box of a Concert Harp

The harp is a multi-stringed musical instrument that has its strings connected directly to a sound box. The sound box is the means by which the vibrational energy in the strings is radiated as sound. The sound box has its own distinctive vibrational structure unrelated to that of the strings, and thus it contributes to the acoustic character of the instrument.

Structure of a Concert Harp

All string instruments have a set of thin, taut strings that vibrate at a fundamental frequency with many harmonic overtones. On a harp these strings are set into vibration by plucking, and this vibration is transmitted to a soundboard, which anchors one end of each string. The basic phenomenology of string motion is dealt with in standard textbooks, although many aspects are still poorly understood. Fig. 1 shows how harp strings move after plucking, whirling around in small ellipses. It is this motion that excites the soundboard into vibration and causes it to radiate sound. The easiest way to see the motion is to pluck some of the lower strings under illumination from a fluorescent light. Fluorescent lights flicker at 120 Hz, giving a stroboscopic effect that appears to stop the string motion at various points in each cycle of vibration.

Fig.1. Vibrating strings of a Gothic Harp: note the elliptical motion of the plucked string on the right.

Strings define the musical note, but they are thin and cannot move much air and therefore produce little sound on their own. It is the sound box that produces the necessary volume of sound. All sound boxes consist of a thin shell, usually wooden, with a hole – or several holes in the case of a harp. Harp sound holes usually do double-duty as a means to attach strings, unless the harp is pre-1750 and the strings attach from the front. However, even old harps have sound holes, and their presence is crucial. This article attempts to explain why harp sound boxes are wooden structures with holes, and suggests a simple experiment to demonstrate how they work.

How Soundboxes Work

There is five thousand years of evolution behind the modern harp, from the Pu-Abi harp to the present, and the salient features of the sound box are as follows. First of all the sound box should be as large as is practically possible, because large areas radiate sound better than small ones do. Secondly, the sound box should be light, because it has to be driven to vibrate by strings of very small mass. Thirdly, it has to be very strong to withstand the string tension. The second and third requirements sit uneasily together, but this is a common engineering dilemma: light is easy, strong is easy, but both is hard. Airplanes and boats have the same problem, which is why the inside of a harp sound box bears some resemblance to the monocoque shell of a kayak or an aircraft fuselage. Lastly and more subtley, it has to radiate sound well over a broad range of frequencies, and this is where the holes come in.

Any box made out of a stiff material will vibrate at a number of different frequencies, depending on how it is excited. Tap any container like an empty coffee tin in various places and listen; different tones will be heard. These frequencies in general bear no relationship to those of a musically defined scale (unless of course the structure is a Trinidadian Steelpan, in which case great effort has gone into ensuring that it does). The trick is make a sound box vibrate in ranges of frequencies by spreading the vibrational frequencies out to include those that the strings are trying to excite; this is where the enclosed air and the sound holes become very important.

The purpose of a sound box is to take the vibrational energy of a string and radiate it as sound. For various reasons it is relatively easy to do this efficiently at the higher frequencies of the audible range (particularly over 1000 Hz). It is much easier to shout at high frequencies than at low ones. In addition the ear is very sensitive to high frequencies, another reason why electronic alarms have annoying high pitches. As a result, instrument makers put their most strenuous efforts into radiating sound at the low end of the audible range – around 100-500 Hz – a range that is crucial to the character of the instrument’s sound. Consider a sound box of any string instrument: the two most important vibrating parts here are the top plate (the one attached to the strings, i.e. the soundboard) and the enclosed air. These two parts behave like two pendulums connected with a floppy spring, or what physicists call "coupled oscillators", as shown in Fig.2.

Fig.2. Two lowest vibration modes of coupled pendula. When the pair swing in the same direction, they do so at a lower frequency than when they swing in opposite directions. In our analogy, consider the left pendulum to be the soundboard, the right pendulum to be the air in the necks of the sound holes, and spring to be the bulk of the air in the soundbox.

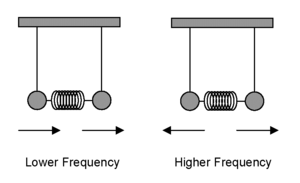
Coupled Oscillator Model

There are two primary ways these pendula can oscillate – both in the same direction or each in the opposite direction from the other; these motions are “normal modes”. The mode where the pendula vibrate in the same direction has a lower frequency than when they are moving opposite to each other. In the former case the spring isn’t playing a part, but in the latter case it is.

Now consider a harp sound box. Push down on the top plate and a small amount of air squeezes out of the sound holes at the back (Fig.3a). When the top plate is tapped, the plate vibrates up and down for a second or so. The air does likewise, like the air in the neck of a bottle vibrates when blown over the top. When the plate moves inward, the air moves out, just as two pendula moving in the same direction. This simple mechanism works at low frequencies – about 150 Hz or less typically. At higher frequencies, at about 200 Hz, the air vibration lags behind that of the plate and starts to move in when the plate moves in, and out when the plate moves outwards (Fig. 3b). In the pendulum analogy, consider the left pendulum to be the soundboard, the right pendulum to be the air in the necks of the soundholes, and spring to be the bulk of the air in the sound box. Unlike the pendulum diagram, the moving parts of the harp are not the same; the mobile part of the soundboard weighs several hundred grams (of the order of a pound) whereas only about 5 grams of air moves (the weight of two pennies). If the masses were closer together in size, the spread between the frequencies of the two modes would be too great.

Fig.3. Primary vibrational motion of a harp soundboard and the air in the necks of the soundholes: (a) soundboard out, air in and vice versa (lower frequency); (b) soundboard out, air out and vice versa (higher frequency).

Sound Radiation

The low frequency interaction of air and sound box produces two modes which radiate a lot of sound at their two resonant frequencies. The vibration of the soundboard is transmitted to surrounding air, and the air vibration in the sound holes produces sound directly. Due to energy losses in the wood, these are not well-defined frequencies, and the instrument radiates fairly well between these two frequencies also. The frequency spread is one reason a wood like spruce is preferred for soundboards: it is resonant but not too resonant. A sheet of aluminum would be stronger and more resonant, but would only vibrate at very well-defined frequencies and not the ranges of frequencies we desire. It is easier to produce sound at high frequencies than low, and thus this mechanism also radiates sound well above 200 Hz. So here is a way of ensuring that the instrument works over a broad range of low frequencies. A simple experiment is to put masking tape over the of a guitar or violin, or by block the sound holes of a harp with thick pieces of styrofoam, and to note how the sound quality changes.

To summarize, what the holes do is to spread out the resonant frequencies of the sound box, so the strings can set the air around the sound box in motion and thus produce audible sound. The frequency spread is achieved by coupling the soundboard to a small amount of air in the necks of the sound holes that can move with or against the soundboard. For more technical details on this mechanism, see Ref..

See Also

• Harp
• Strings
• Sound board