Course:PHYS350/Small Oscillations and Perturbed Motion

In Linear Motion, we argued that all sufficiently small oscillations are harmonic. In this section we will exploit this result in several ways to understand

1. The motion of systems with many degrees of freedom near equilibrium,
2. The motion of systems perturbed from known solutions, and
3. The motion of systems with Lagrangians perturbed from systems with known solutions.

All three of these points are applications of perturbation theory, and they all start with the harmonic oscillator.

Normal Modes

The modes of oscillation of systems near equilibrium are called the normal modes of the system. Understanding the frequencies of the normal modes of the system is crucial to design a system that can move (even it isn't meant to). Let's look at a system with many degrees of freedom; we have

$L={\frac {1}{2}}\sum _{i,j}T_{ij}{\dot {q}}_{i}{\dot {q}}_{j}-V\left(q_{1},\ldots q_{n}\right).$

Let $q_{0,i}$ be an equilibrium position and expand about this point $q_{i}=q_{0,i}+\eta _{i}$ so ${\dot {q}}_{i}={\dot {\eta }}_{i}$.

We can expand the potential energy to give

$V\left(q_{1},\ldots q_{n}\right)=V\left(q_{0,1},\ldots q_{0,n}\right)+\sum _{i}\left({\frac {\partial V}{\partial q_{i}}}\right)_{q_{0,i}}\eta _{i}+{\frac {1}{2}}\sum _{i,j}\left({\frac {\partial ^{2}V}{\partial q_{i}\partial q_{j}}}\right)_{q_{0,i}}\eta _{i}\eta _{j}+\cdots .$

The first term is a constant with respect to $\eta _{i}$ and constant terms do not affect the motion. The second term is zero, because $q_{0,i}$ is a point of equilibrium so we are left with

$L={\frac {1}{2}}\sum _{i,j}\left(T_{ij}{\dot {\eta }}_{i}{\dot {\eta }}_{j}-V_{ij}\eta _{i}\eta _{j}\right)$

where

$T_{ij}=T_{ij}\left(q_{0,1},\ldots q_{0,n}\right)$ and $V_{ij}=\left({\frac {\partial ^{2}V}{\partial q_{i}\partial q_{j}}}\right)_{q_{0,i}},$

yielding the equations of motion

$\sum _{j}\left(T_{ij}{\ddot {\eta }}_{j}-V_{ij}\eta _{j}\right)=0$

This is a linear differential equation with constant coefficients. We can try the solution

$\eta _{i}=Ca_{i}e^{-i\omega t}$

so we have

$\sum _{j}\left(V_{ij}a_{j}-\omega ^{2}T_{ij}a_{j}\right)=0.$

This is a matrix equation such that

${\vec {\vec {A}}}\cdot {\vec {a}}=0$ with

${\vec {a}}=\left[{\begin{matrix}a_{1}\\a_{2}\\\vdots \\a_{j}\end{matrix}}\right]$

and

${\vec {\vec {A}}}=\left[{\begin{matrix}V_{11}-\omega ^{2}T_{11}&V_{12}-\omega ^{2}T_{12}&\cdots \\V_{21}-\omega ^{2}T_{21}&V_{22}-\omega ^{2}T_{22}&\cdots \\\vdots &&\end{matrix}}\right]$

This equation only has a solution is $\det {\vec {\vec {A}}}=0$. This gives a $n$th-degree polynomial to solve for $\omega ^{2}$. We will get $n$ solutions for $\omega ^{2}$ that we can substitute into the matrix equation and solve for $a_{j}$.

Is this guaranteed to work? Yes, it turns out. Look at the equation in terms of matrices we have

${\vec {\vec {V}}}{\vec {a}}=\omega ^{2}{\vec {\vec {T}}}{\vec {a}}.$

The matrix ${\vec {\vec {V}}}$ is symmetric and real. The matrix ${\vec {\vec {T}}}$ should be positive definite (because a negative kinetic energy doesn't make sense). Technical issue: If ${\vec {\vec {T}}}$ has a null space, the degrees of freedom corresponding to the null space are massless and cannot be excited unless they are in the null space of ${\vec {\vec {V}}}$. Either way, you can drop the null space from both sides of the equation.

Assuming that ${\vec {\vec {T}}}$ is invertable we have

$\left({\vec {\vec {T}}}\right)^{-1}{\vec {\vec {V}}}{\vec {a}}=\omega ^{2}{\vec {a}}$

and we have a standard eigenvalue equation. In most examples, the kinetic energy matrix will be diagonal, so it is straightforward to construct the quotient matrix and diagonize it.

Perturbations about Steady Motion

Let's say I have some solution to the equations of motion and I would like to look at small deviations from the solution. Let's $q_{0,i}(t)$ satisfy

${\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {q}}_{i}}}-{\frac {\partial L}{\partial q_{i}}}=0,$

and let's look at

$q_{i}(t)=q_{0,i}(t)+\eta _{i}(t)$

where $\eta _{i}$ is small. Let's expand the entire Lagrangian to find the equations of motion for the deviations $\eta _{i}$. We have

$L\left(q_{1},\ldots q_{n}\right)=L\left(q_{0,1},\ldots q_{0,n};{\dot {q}}_{0,1},\ldots {\dot {q}}_{0,n}\right)+\sum _{i}\left[\left({\frac {\partial L}{\partial q_{i}}}\right)_{q_{0,i}}\eta _{i}+\left({\frac {\partial L}{\partial {\dot {q}}_{i}}}\right)_{q_{0,i}}{\dot {\eta }}_{i}\right]+$

                ${\frac {1}{2}}\sum _{i,j}\left[\left({\frac {\partial ^{2}L}{\partial q_{i}\partial q_{j}}}\right)_{q_{0,i}}\eta _{i}\eta _{j}+\left({\frac {\partial ^{2}L}{\partial {\dot {q}}_{i}\partial {\dot {q}}_{j}}}\right)_{q_{0,i}}{\dot {\eta }}_{i}{\dot {\eta }}_{j}+2\left({\frac {\partial ^{2}L}{\partial q_{i}\partial {\dot {q}}_{j}}}\right)_{q_{0,i}}\eta _{i}{\dot {\eta }}_{j}\right]+\cdots .$

Now let's apply Lagrange's equations for the deviations

${\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {\eta }}_{i}}}-{\frac {\partial L}{\partial \eta _{i}}}=0$

to give

${\frac {d}{dt}}\left\{\left({\frac {\partial L}{\partial {\dot {q}}_{j}}}\right)_{q_{0,i}}+\sum _{i}\left[\left({\frac {\partial ^{2}L}{\partial {\dot {q}}_{i}\partial {\dot {q}}_{j}}}\right)_{q_{0,i}}{\dot {\eta }}_{i}+\left({\frac {\partial ^{2}L}{\partial q_{i}\partial {\dot {q}}_{j}}}\right)_{q_{0,i}}\eta _{i}\right]\right\}$

        $-\left({\frac {\partial L}{\partial q_{j}}}\right)_{q_{0,i}}-\sum _{i}\left[\left({\frac {\partial ^{2}L}{\partial q_{i}\partial q_{j}}}\right)_{q_{0,i}}\eta _{i}+\left({\frac {\partial ^{2}L}{\partial q_{i}\partial {\dot {q}}_{j}}}\right)_{q_{0,i}}{\dot {\eta }}_{i}\right]=0$

The two terms without $\eta$ actually cancel each other out, leaving the following equations of motion.

${\frac {d}{dt}}\left\{\sum _{i}\left[\left({\frac {\partial ^{2}L}{\partial {\dot {q}}_{i}\partial {\dot {q}}_{j}}}\right)_{q_{0,i}}{\dot {\eta }}_{i}+\left({\frac {\partial ^{2}L}{\partial q_{i}\partial {\dot {q}}_{j}}}\right)_{q_{0,i}}\eta _{i}\right]\right\}$

        $-\sum _{i}\left[\left({\frac {\partial ^{2}L}{\partial q_{i}\partial q_{j}}}\right)_{q_{0,i}}\eta _{i}+\left({\frac {\partial ^{2}L}{\partial q_{i}\partial {\dot {q}}_{j}}}\right)_{q_{0,i}}{\dot {\eta }}_{i}\right]=0.$

In steady motion, the partial derivatives are taken to be constant in time yielding the even simpler result

$\sum _{i}\left[\left({\frac {\partial ^{2}L}{\partial {\dot {q}}_{i}\partial {\dot {q}}_{j}}}\right)_{q_{0,i}}{\ddot {\eta }}_{i}-\left({\frac {\partial ^{2}L}{\partial q_{i}\partial q_{j}}}\right)_{q_{0,i}}\eta _{i}\right]=0.$

Again we have a linear differential equation with constant coefficients, and all of the results from the previous section carry over.

Perturbed Lagrangians

What about finding solutions to Lagrangians that are almost like ones that we have already solved? Let's say we have

$L=L_{0}+L_{1}$

where $L_{1}$ is considered to be small compared to $L_{0}$ Let's say I have some solution to the equations of motion for $L_{0}$ and I would like to look at small deviations from the solution induced by the change in the Lagrangian. Let's say $q_{0,i}(t)$ satisfy

${\frac {d}{dt}}{\frac {\partial L_{0}}{\partial {\dot {q}}_{i}}}-{\frac {\partial L_{0}}{\partial q_{i}}}=0,$

and let's look at

$q_{i}(t)=q_{0,i}(t)+\eta _{i}(t)$

where $\eta _{i}$ is small. Let's expand the entire Lagrangian to find the equations of motion for the deviations $\eta _{i}$. We have

$L\left(q_{1},\ldots q_{n}\right)=L\left(q_{0,1},\ldots q_{0,n};{\dot {q}}_{0,1},\ldots {\dot {q}}_{0,n}\right)+\sum _{i}\left[\left({\frac {\partial L}{\partial q_{i}}}\right)_{q_{0,i}}\eta _{i}+\left({\frac {\partial L}{\partial {\dot {q}}_{i}}}\right)_{q_{0,i}}{\dot {\eta }}_{i}\right]+$

                ${\frac {1}{2}}\sum _{i,j}\left[\left({\frac {\partial ^{2}L}{\partial q_{i}\partial q_{j}}}\right)_{q_{0,i}}\eta _{i}\eta _{j}+\left({\frac {\partial ^{2}L}{\partial {\dot {q}}_{i}\partial {\dot {q}}_{j}}}\right)_{q_{0,i}}{\dot {\eta }}_{i}{\dot {\eta }}_{j}+2\left({\frac {\partial ^{2}L}{\partial q_{i}\partial {\dot {q}}_{j}}}\right)_{q_{0,i}}\eta _{i}{\dot {\eta }}_{j}\right]+$

                $L_{1}\left(q_{0,1},\ldots q_{0,n};{\dot {q}}_{0,1},\ldots {\dot {q}}_{0,n}\right)+\sum _{i}\left[\left({\frac {\partial L_{1}}{\partial q_{j}}}\right)_{q_{0,i}}\eta _{i}+\left({\frac {\partial L_{1}}{\partial {\dot {q}}_{j}}}\right)_{q_{0,i}}{\dot {\eta }}_{i}\right]+\cdots .$

Now let's apply Lagrange's equations for the deviations

${\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {\eta }}_{i}}}-{\frac {\partial L}{\partial \eta _{i}}}=0$

to give

${\frac {d}{dt}}\left\{\left({\frac {\partial L_{0}}{\partial {\dot {q}}_{j}}}\right)_{q_{0,i}}+\left({\frac {\partial L_{1}}{\partial {\dot {q}}_{j}}}\right)_{q_{0,i}}+\sum _{i}\left[\left({\frac {\partial ^{2}L_{0}}{\partial {\dot {q}}_{i}\partial {\dot {q}}_{j}}}\right)_{q_{0,i}}{\dot {\eta }}_{i}+\left({\frac {\partial ^{2}L_{0}}{\partial q_{i}\partial {\dot {q}}_{j}}}\right)_{q_{0,i}}\eta _{i}\right]\right\}$

        $-\left({\frac {\partial L_{0}}{\partial q_{j}}}\right)_{q_{0,i}}+\left({\frac {\partial L_{1}}{\partial q_{j}}}\right)_{q_{0,i}}+\sum _{i}\left[\left({\frac {\partial ^{2}L_{0}}{\partial q_{i}\partial q_{j}}}\right)_{q_{0,i}}\eta _{i}+\left({\frac {\partial ^{2}L_{0}}{\partial q_{i}\partial {\dot {q}}_{j}}}\right)_{q_{0,i}}{\dot {\eta }}_{i}\right]=0$

The two lowest orders terms without $\eta$ actually cancel each other out, leaving the following equations of motion.

${\frac {d}{dt}}\left\{\sum _{i}\left[\left({\frac {\partial ^{2}L_{0}}{\partial {\dot {q}}_{i}\partial {\dot {q}}_{j}}}\right)_{q_{0,i}}{\dot {\eta }}_{i}+\left({\frac {\partial ^{2}L_{0}}{\partial q_{i}\partial {\dot {q}}_{j}}}\right)_{q_{0,i}}\eta _{i}\right]\right\}$

        $-\sum _{i}\left[\left({\frac {\partial ^{2}L_{0}}{\partial q_{i}\partial q_{j}}}\right)_{q_{0,i}}\eta _{i}+\left({\frac {\partial ^{2}L_{0}}{\partial q_{i}\partial {\dot {q}}_{j}}}\right)_{q_{0,i}}{\dot {\eta }}_{i}\right]=\left({\frac {\partial L_{1}}{\partial q_{j}}}\right)_{q_{0,i}}-{\frac {d}{dt}}\left({\frac {\partial L_{1}}{\partial {\dot {q}}_{j}}}\right)_{q_{0,i}}.$

Let's specialize and assume that the unperturbed motion is steady so the partial derivatives of the unperturbed Lagrangian are constant in time, to obtain

$\sum _{i}\left[\left({\frac {\partial ^{2}L_{0}}{\partial {\dot {q}}_{i}\partial {\dot {q}}_{j}}}\right)_{q_{0,i}}{\ddot {\eta }}_{i}-\left({\frac {\partial ^{2}L_{0}}{\partial q_{i}\partial q_{j}}}\right)_{q_{0,i}}\eta _{i}\right]=\left({\frac {\partial L_{1}}{\partial q_{j}}}\right)_{q_{0,i}}-{\frac {d}{dt}}\left({\frac {\partial L_{1}}{\partial {\dot {q}}_{j}}}\right)_{q_{0,i}}.$

which is the equation of a coupled set of driven harmonic oscillators.

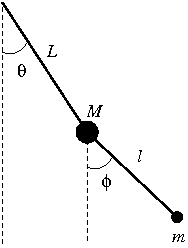
Examples

Double Pendulum

The kinetic energy is

$T={\frac {1}{2}}ML^{2}{\dot {\theta }}^{2}+{\frac {1}{2}}m\left[L^{2}{\dot {\theta }}^{2}+l^{2}{\dot {\phi }}^{2}+2Ll{\dot {\theta }}{\dot {\phi }}\cos \left(\phi -\theta \right)\right].$

If we take the small angle approximation we have

$T={\frac {1}{2}}ML^{2}{\dot {\theta }}^{2}+{\frac {1}{2}}m\left(L^{2}{\dot {\theta }}^{2}+l^{2}{\dot {\phi }}^{2}+2Ll{\dot {\theta }}{\dot {\phi }}\right)={\frac {1}{2}}ML^{2}{\dot {\theta }}^{2}+{\frac {1}{2}}m\left(L{\dot {\theta }}+l{\dot {\phi }}\right)^{2},$

so we can define the orthogonal coordinates,

$q_{1}={\sqrt {M}}L\theta ,q_{2}={\sqrt {m}}\left(L\theta +l\phi \right)$

and

$T={\frac {1}{2}}{\dot {q}}_{1}^{2}+{\frac {1}{2}}{\dot {q}}_{2}^{2}$

Let's write out the potential energy,

$V=\left(M+m\right)gL\left(1-\cos \theta \right)+mgl\left(1-\cos \phi \right)$

and in the small angle approximation

$V={\frac {1}{2}}\left(M+m\right)gL\theta ^{2}+{\frac {1}{2}}mgl\phi ^{2}={\frac {1}{2}}{\frac {M+m}{M}}{\frac {g}{L}}q_{1}^{2}+{\frac {1}{2}}m{\frac {g}{l}}\left({\frac {q_{2}}{\sqrt {m}}}-{\frac {q_{1}}{\sqrt {M}}}\right)^{2}.$

Let's now write out the equations of motion

${\ddot {q}}_{1}+{\frac {M+m}{M}}{\frac {g}{L}}q_{1}-{\frac {m}{\sqrt {M}}}{\frac {g}{l}}\left({\frac {q_{2}}{\sqrt {m}}}-{\frac {q_{1}}{\sqrt {M}}}\right)=0$

${\ddot {q}}_{2}+{\sqrt {m}}{\frac {g}{l}}\left({\frac {q_{2}}{\sqrt {m}}}-{\frac {q_{1}}{\sqrt {M}}}\right)=0$

We can write this as a matrix equation,

$\left[{\begin{matrix}{\ddot {q}}_{1}\\{\ddot {q}}_{2}\end{matrix}}\right]=\left[{\begin{matrix}-{\frac {M+m}{M}}{\frac {g}{L}}-{\frac {m}{M}}{\frac {g}{l}}&{\frac {g}{l}}{\sqrt {\frac {m}{M}}}\\{\sqrt {\frac {m}{M}}}{\frac {g}{l}}&-{\frac {g}{l}}\end{matrix}}\right]\left[{\begin{matrix}q_{1}\\q_{2}\end{matrix}}\right].$

Now let's substitute the solution $q_{\alpha }=A_{\alpha }e^{i\omega t}$ to get

$\left[{\begin{matrix}{\frac {M+m}{M}}{\frac {g}{L}}+{\frac {m}{M}}{\frac {g}{l}}-\omega ^{2}&-{\frac {g}{l}}{\sqrt {\frac {m}{M}}}\\-{\sqrt {\frac {m}{M}}}{\frac {g}{l}}&{\frac {g}{l}}-\omega ^{2}\end{matrix}}\right]\left[{\begin{matrix}A_{1}\\A_{2}\end{matrix}}\right]=0.$

We have the characteristic equation

$\left({\frac {M+m}{M}}{\frac {g}{L}}+{\frac {m}{M}}{\frac {g}{l}}-\omega ^{2}\right)\left({\frac {g}{l}}-\omega ^{2}\right)-{\frac {g^{2}}{l^{2}}}{\frac {m}{M}}=0$

or

$\omega ^{4}-\omega ^{2}\left({\frac {M+m}{M}}{\frac {g}{L}}+{\frac {m}{M}}{\frac {g}{l}}+{\frac {g}{l}}\right)+{\frac {M+m}{M}}{\frac {g^{2}}{Ll}}+{\frac {m}{M}}{\frac {g^{2}}{l^{2}}}-{\frac {g^{2}}{l^{2}}}{\frac {m}{M}}=0$

$\omega ^{4}-\omega ^{2}\left[{\frac {M+m}{M}}g\left({\frac {1}{L}}+{\frac {1}{l}}\right)\right]+{\frac {M+m}{M}}{\frac {g^{2}}{Ll}}=0$

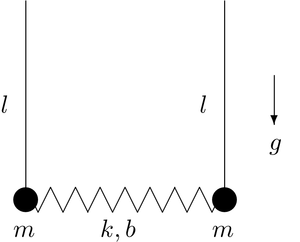
Coupled Pendulums

Coupled Pendulums

Let's use the horizontal displacements of the two pendulum bobs as our coordinates ($x_{1}$ and $x_{2}$). When the bobs are vertical they are an equilibrium distance $b$ apart. The vertical position of the bobs are

$y_{1}=l-{\sqrt {l^{2}-x_{1}^{2}}}$ and $y_{2}=l-{\sqrt {l^{2}-x_{2}^{2}}}$.

The distance between the bobs is

$d^{2}=\left(x_{2}-x_{1}+b\right)^{2}+\left(y_{2}-y_{1}\right)^{2}.$

We can write the potential energy as

$V=mgy_{1}+mgy_{2}+{\frac {1}{2}}k\left(d-b\right)^{2}\approx {\frac {1}{2}}m{\frac {g}{l}}\left(x_{1}^{2}+x_{2}^{2}\right)+{\frac {1}{2}}k\left(x_{2}-x_{1}\right)^{2}.$

Let's write the kinetic energy, we have

$T={\frac {1}{2}}m\left({\dot {x}}_{1}^{2}+{\dot {x}}_{2}^{2}+{\dot {y}}_{1}^{2}+{\dot {y}}_{2}^{2}\right)\approx {\frac {1}{2}}m\left({\dot {x}}_{1}^{2}+{\dot {x}}_{2}^{2}\right).$

Let's write out the equations of motion,

${\ddot {x}}_{1}+\omega _{0}^{2}x_{1}-\omega _{c}^{2}\left(x_{2}-x_{1}\right)=0$

${\ddot {x}}_{2}+\omega _{0}^{2}x_{2}+\omega _{c}^{2}\left(x_{2}-x_{1}\right)=0$

where $\omega _{0}^{2}=g/l$ and $\omega _{c}^{2}=k/m$. Let's substitute $x_{\alpha }=A_{\alpha }e^{i\omega t}$ and write the result as a matrix equation,

$\left[{\begin{matrix}-\omega ^{2}+\omega _{0}^{2}+\omega _{c}^{2}&-\omega _{c}^{2}\\-\omega _{c}^{2}&-\omega ^{2}+\omega _{0}^{2}+\omega _{c}^{2}\end{matrix}}\right]\left[{\begin{matrix}A_{1}\\A_{2}\end{matrix}}\right]=0$

If $\omega ^{2}=\omega _{0}^{2}$ we have $A_{1}=A_{2}$. If $\omega ^{2}=\omega _{0}^{2}+2\omega _{c}^{2}$ we have $A_{1}=-A_{2}$.

Central Force

Let's try to find the equations for small perturbations to a central force whose potential is a power-law of radius. We have the following Lagrangian,

$L={\frac {1}{2}}\left({\dot {r}}^{2}+r^{2}{\dot {\theta }}^{2}\right)+kr^{\alpha }.$

Let's find the steady solution first (${\dot {r}}=0$). we have

${\ddot {r}}-r{\dot {\theta }}^{2}-\alpha kr^{\alpha -1}=0$

so

${\dot {\theta }}^{2}\equiv \Omega ^{2}=-\alpha kr_{0}^{\alpha -2}.$

For the θ-equation we have

${\frac {d}{dt}}\left(r^{2}{\dot {\theta }}\right)=0$

so ${\dot {\theta }}$ is constant if the radius is constant.

Let's take

$r(t)=r_{0}+\eta _{1}(t),\theta (t)=\Omega t+\eta _{2}(t)$

and substitute into the Lagrangian,

$L={\frac {1}{2}}\left[{\dot {\eta }}_{1}^{2}+\left(r_{0}+\eta _{1}\right)^{2}\left(\Omega +{\dot {\eta }}_{2}\right)^{2}\right]+kr_{0}^{\alpha }\left(1+{\frac {\eta _{1}}{r_{0}}}\right)^{\alpha }={\frac {1}{2}}\left[{\dot {\eta }}_{1}^{2}+\left(r_{0}+\eta _{1}\right)^{2}\left(\Omega +{\dot {\eta }}_{2}\right)^{2}\right]-{\frac {\Omega ^{2}r_{0}^{2}}{\alpha }}\left(1+{\frac {\eta _{1}}{r_{0}}}\right)^{\alpha }.$

According to the rules of perturbation theory, we can drop all the terms that are constant and linear in $\eta$ and keep the second order terms to get

$L={\frac {1}{2}}\left[{\dot {\eta }}_{1}^{2}+r_{0}^{2}{\dot {\eta }}_{2}^{2}+\eta _{1}^{2}\Omega ^{2}+4r_{0}\Omega \eta _{1}{\dot {\eta }}_{2}\right]-{\frac {\Omega ^{2}(\alpha -1)}{2}}\eta _{1}^{2}$

Now let's get the equations of motion, we have

${\ddot {\eta }}_{1}=2r_{0}\Omega {\dot {\eta }}_{2}-\left(\alpha +2\right)\Omega ^{2}\eta _{1}$

and

${\frac {d}{dt}}\left(r_{0}^{2}{\dot {\eta }}_{2}+2r_{0}\Omega \eta _{1}\right)=0$

so

${\dot {\eta }}_{2}={\frac {p_{2}-2r_{0}\Omega \eta _{1}}{r_{0}^{2}}}$

which we can substitute into the equation for $\eta _{1}$ to get

${\ddot {\eta }}_{1}=2r_{0}\Omega {\frac {p_{2}-2r_{0}\Omega \eta _{1}}{r_{0}^{2}}}-\left(\alpha -2\right)\Omega ^{2}\eta _{1}={\frac {2\Omega p_{2}}{r_{0}}}-4\Omega ^{2}\eta _{1}-\left(\alpha -2\right)\Omega ^{2}\eta _{1}$

${\ddot {\eta }}_{1}={\frac {2\Omega p_{2}}{r_{0}}}-\left(\alpha +2\right)\Omega ^{2}\eta _{1}=-\left(\alpha +2\right)\Omega ^{2}\left[{\frac {2p_{2}}{r_{0}(\alpha +2)\Omega }}-\eta _{1}\right]$

so

$\eta _{1}=A\cos \left({\sqrt {\alpha +2}}\Omega t\right)+{\frac {2p_{2}}{r_{0}(\alpha +2)\Omega }}$

Anharmonic Oscillator

The final type of problem that one can treat in perturbation theory is a perturbation to the Lagrangian itself. As an example we shall do the aharmonic oscillator

$L={\frac {1}{2}}m{\dot {x}}^{2}-{\frac {1}{2}}m\omega _{0}^{2}x^{2}-{\frac {1}{3}}m\alpha x^{3}-{\frac {1}{4}}m\beta x^{4}$

which yields the equation of motion

${\ddot {x}}+\omega _{0}^{2}x=-\alpha x^{2}-\beta x^{3}$

Let's look for a solution as a series of approximations

$x=x^{(1)}+x^{(2)}+x^{(3)}+\cdot$

and

$\omega =\omega _{0}+\omega ^{(1)}+\omega ^{(2)}+\cdot$

where there are corrections to both the function dependence of the motion and the frequency of the oscillations. Let's rewrite the equation of motion a bit

${\frac {\omega _{0}^{2}}{\omega ^{2}}}{\ddot {x}}+\omega _{0}^{2}x=-\alpha x^{2}-\beta x^{3}-\left(1-{\frac {\omega _{0}^{2}}{\omega ^{2}}}\right){\ddot {x}}$

The way that we solve such a differential equation is to substitute the trial solution into it and group the terms according to the sum of their superscripts and consider each bunch of terms a separate equation to solve. Let's look at the first order terms:

First-order terms

$-{\frac {\omega _{0}^{2}}{\omega ^{2}}}\omega ^{2}a\cos \omega t+\omega _{0}^{2}a\cos \omega t=0.$

All of the terms on the right-hand side have superscripts that add to more than one. This equation is satisfied identically.

Second-order terms

${\frac {\omega _{0}^{2}}{\omega ^{2}}}{\ddot {x}}^{(2)}+\omega _{0}^{2}{\ddot {x}}^{(2)}=-\alpha \left(x^{(1)}\right)^{2}+2\omega \omega ^{(1)}x^{(1)}.$

${\frac {\omega _{0}^{2}}{\omega ^{2}}}{\ddot {x}}^{(2)}+\omega _{0}^{2}{\ddot {x}}^{(2)}=-\alpha \left(a\cos \omega t\right)^{2}+2\omega \omega ^{(1)}a\cos \omega t.$

${\frac {\omega _{0}^{2}}{\omega ^{2}}}{\ddot {x}}^{(2)}+\omega _{0}^{2}{\ddot {x}}^{(2)}=-{\frac {\alpha a^{2}}{2}}\left(1+\cos 2\omega t\right)+2\omega \omega ^{(1)}a\cos \omega t.$

This is the equation for a driven harmonic oscillator. The final term drives the oscillator at its natural frequency ($\omega$). This would cause the perturbation to grow without bound which doesn't make sense; it violates perturbation theory but we have the freedom to make the final term go away by taking

$\omega ^{(1)}=0$

so the frequency is unchanged at this order. To solve for the terms that remain, we take the particular solution to the differential equation. The solution to homogenous looks just like $x^{(1)}$, so it is already included. We have

$x^{(2)}=-{\frac {\alpha a^{2}}{2\omega _{0}^{2}}}+{\frac {\alpha a^{2}}{6\omega _{0}^{2}}}\cos 2\omega t.$

Third-order terms

${\frac {\omega _{0}^{2}}{\omega ^{2}}}{\ddot {x}}^{(3)}+\omega _{0}^{2}{\ddot {x}}^{(3)}=-2\alpha x^{(1)}x^{(2)}-\beta \left(x^{(1)}\right)^{3}+2\omega \omega ^{(2)}x^{(1)}.$

We can write all of the terms on the right-hand side as a sum of a constant, a term proportional to $\cos \omega$ and $\cos 3\omega t$ to give

${\frac {\omega _{0}^{2}}{\omega ^{2}}}{\ddot {x}}^{(3)}+\omega _{0}^{2}{\ddot {x}}^{(3)}=a^{2}\left({\frac {\beta }{4}}-{\frac {\alpha ^{2}}{6\omega _{0}^{2}}}\right)\cos 3\omega t+a\left(2\omega _{0}\omega ^{(2)}+{\frac {5a^{2}\alpha ^{2}}{6\omega _{0}^{2}}}-{\frac {3}{4}}a^{2}\beta \right)\cos \omega t.$

As before we would like for the final term to vanish so we take

$\omega ^{(2)}=\left({\frac {3\beta }{8\omega _{0}}}-{\frac {5\alpha ^{2}}{12\omega _{0}^{3}}}\right)a^{2}$

and we solve for $x^{(3)}$ as before to give

$x^{(3)}={\frac {a^{3}}{16\omega _{0}^{2}}}\left({\frac {\alpha ^{2}}{3\omega _{0}^{2}}}-{\frac {\beta }{2}}\right)\cos 3\omega t.$

If we combine these results we see that we can use how the period of the oscillation changes with amplitude or the relative size of the various harmonics to determine the anharmonic terms in the Lagrangian.