1. A particle of mass  moves under a conservative force with a potential energy function given by
moves under a conservative force with a potential energy function given by

where  and
and  are constants, and
are constants, and  . What is the force on the particle? Sketch the function
. What is the force on the particle? Sketch the function  , for both cases
, for both cases  and
and  , and describe the possible types of motion.
, and describe the possible types of motion.
Let's take  and we have a particle initial in the region
and we have a particle initial in the region  , moving to the right with velocity
, moving to the right with velocity  . When it emerges into the region
. When it emerges into the region  , will it do so earlier or later than if it were moving freely under no force? Find an expression for the time difference. (To do the required integral, try the substitution
, will it do so earlier or later than if it were moving freely under no force? Find an expression for the time difference. (To do the required integral, try the substitution  where
where  is some constant.
is some constant.
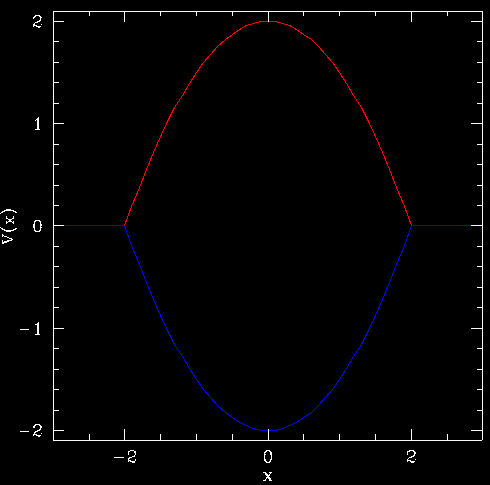
Red is  and blue is
and blue is 
The different types of motion for  are
are
 , motion is restricted to the left or right side. The particle will bounce off of the hill.
, motion is restricted to the left or right side. The particle will bounce off of the hill. , the particle can climb over the hill (slowing on the way up) and end up on the other side.
, the particle can climb over the hill (slowing on the way up) and end up on the other side.
The different types of motion for  are
are
 , motion is restricted to well. It oscillates harmonically back and forth.
, motion is restricted to well. It oscillates harmonically back and forth. , the particle will escape to infinity.
, the particle will escape to infinity.
The time to go pass the hill if it were not there is simply  . The time to go over the hill is
. The time to go over the hill is

Let's make the substitution that  to get
to get

Therefore the time difference is

As  the time difference vanishes. As
the time difference vanishes. As  from above, the time difference diverges.
from above, the time difference diverges.
2. A particle of mass  is attached to a string of length
is attached to a string of length  . The particle moves in a horizontal plane without friction, and the string passes through a hole in the centre of the plane and is attached to another object of mass
. The particle moves in a horizontal plane without friction, and the string passes through a hole in the centre of the plane and is attached to another object of mass  below the plane that only moves vertically under the Earth's gravitational field. Write out the Lagrangian for this system and derive the equations of motion. What quantities are conserved?
below the plane that only moves vertically under the Earth's gravitational field. Write out the Lagrangian for this system and derive the equations of motion. What quantities are conserved?
The kinetic energy of two particles is

and the potential energy is just

where  and
and  are the polar coordinates of the particle that moves in the plane relative to the hole. The Lagrangian is
are the polar coordinates of the particle that moves in the plane relative to the hole. The Lagrangian is

The total energy ( ) is conserved and the angular momentum
) is conserved and the angular momentum  . The equations of motion are
. The equations of motion are

and





































