Course:PHYS341/Archive/2016wTerm2/TibetanSingingBowl

From UBC Wiki
A collection of antique singing bowls

Vibration of the Tibetan Singing Bowl

The Tibetan singing bowl (also known as the rin gong, Himalayan singing bowl, or suzu gong) originated in Tibet in 500 BCE and its ethereal sound has led to its use in both meditation and chanting[1]. It is classified as an idiophone or bell, but instead of hanging from a yoke or headstock the brass body of the singing bowl may sit on the ground, a stand, or cushion. The instrument may be sounded by either striking the body with a mallet covered in fabric (called a puja) or through friction whereby the puja is rubbed along the circumference of the bowl’s rim, producing harmonic overtones[2]. The vibrations of the Tibetan singing bowl are characterized by a fundamental frequency (first harmonic) and usually two audible harmonic overtones (second and third harmonic)s[3].

Vibration Modes

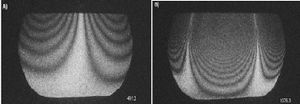
Electronic speckle pattern image of the first two vibration modes of the singing bowl
Diagram showing the first vibration mode of a singing bowl with the antinodes (A) and nodes (N) denoted. The dashed lines show the maximum deformation of the bowl from the equilibrium position as marked by the red line.

Any object that vibrates is characterized by vibration patterns known as modes that occur only at specific frequencies[4]. These modes include vibrating regions referred to as antinodes as well as their non-vibrating regions called nodes. When the rim is rubbed by the puja nodes and loops are created with the nodes always being even in number; alternate loops move in opposite directions[5]. Electronic speckle pattern interferometry allows one to observe these modes[6]. This technique produces a contour map of the motion of a surface. Three patterns usually vibrate at once when the puja strikes the body of the singing bowl. Since there are more than one pattern present at the same time, the resulting motion is complex. The movement of the puja around the bowl changes the volume of the sound making it not a true pure tone; it is modulated so that it rises and falls in intensity as the puja moves around the bowl[7].

Intensity and Frequency of Vibration

When the puja is rubbed along the rim of the Tibetan singing bowl, the fabric that covers the puja will stick and then slip from the bowl in a series of short bursts of motion which create the audible vibrations[8]. The distance between when the puja slips and then sticks to the rim of the bowl is about the diameter of a strand of hair making the puja “jump” even if its motion appears smooth [9]. There is only one pattern of vibration when the puja is traced along the rim of the bowl. The sound will increase in volume when the vibrating part of the bowl is pointed toward the listener. The sound intensity increases and decreases four times four every rotation of the puja, corresponding to the bowl's four separate areas of vibration[10]. Since the fabric covering the head of the puja dampens the vibrations of the bowl, only a single pattern is created as it is rubbed along the rim as opposed to when it is made to strike the bowl’s body. The bowl’s contact with the puja extends past the nodal line into the part of the bowl that is vibrating due to its large diameter, damping the vibrations further[11]. Since the more complex patterns have less space between the areas of maximum vibration, they are damped more heavily than the more simple patterns.

Observation of Vibration Through Fluid Dynamics

Further examination of the vibration patterns of the Tibetan singing bowl may be done by filling the bowl completely with water and then exciting its fundamental deformation mode. The bowl oscillates back and forth between slightly ellipsoidal shapes and the water’s surface vibrates due to the horizontal oscillation of the rim as the puja moves along its circumference[12]. When the amplitude of the rim oscillation is small, axisymmetric capillary waves that have a frequency proportional to that of the excited frequency appear on the water’s surface [13]. When the rim deflection amplitude is increased, waves along the circumference of the bowl appear at the water’s edge. These waves have an amplitude that grows rapidly. The circumferential waves relate to classic edge-induced Faraday waves[14]. The higher the excitation amplitude the more complicated the wave modes. At very high frequencies water droplets are cast off and can be seen to bounce off the water from the edge of the bowl; this is especially true at the anti-node areas. Bouncing water droplets cannot be achieved by merely rubbing the bowl with a puja, a high enough frequency cannot be manually achieved; a constant an even frequency coming from a loudspeaker is capable of producing such a phenomenon[15]. Relation between droplet size and frequency is also observed through fluid dynamics. The size of the droplets is inversely proportional to the frequency; meaning that the higher the frequency the smaller the droplets[16].

Bowl Size and Vibration

For the case of standing waves in a string the frequency of the fundamental harmonic decreases when the length of the string is increased (provided that the tension in the string is kept the same)[17]. From the table below a similar effect for the singing bowls is observed. When the radius of the bowl increases the length of the rim will also increase, meaning that standing waves of longer wavelengths can fit around the rim. This increase in mouth area leads to a decrease in frequency and a lower pitch since waves with longer wavelengths have a lower frequency (v = f • λ). Other factors such as density of the bowl will also affect the pitch, with more dense metals vibrating at a lower frequency[18].

Bowl Radius (cm) First Harmonic Mouth Area (cm^2)
B1 5.9 428 109.4
B2 6 347 113.1
B3 7.5 236 176.7
B4 8.9 187 248.8

[19]

Vibration of Standing Waves

Resonance is a when a vibrating system or external force drives another system to oscillate with greater amplitude at a specific preferential frequency[20]. When a Tibetan singing bowl is filled with water and a loudspeaker nearby is sounded, the resultant vibrations will create standing waves that illustrate an interference pattern called a Chladni pattern. Standing waves are produced by the addition of two identical waves traveling at the same time in opposite directions. These waves will interfere both constructively and destructively with one another as they interact. The resulting waves from the addition of these two waves will form a standing wave in the metal rim. Four antinodes are created by the standing waves as well as four nodes[21]. The nodes have minimal water rippling while the antinodes have the most water motion.

References

  1. ↑ Shrestha, Suren. How to Heal with Singing Bowls. Boulder: Sentient Publications, 2009. Print.
  2. ↑ Shrestha, Suren. How to Heal with Singing Bowls. Boulder: Sentient Publications, 2009. Print.
  3. ↑ August, Brandon. "Dynamics of a Himalayan Singing Bowl." Acoustics.org. Rollins College, 15 May 2012. Web. 2 Feb. 2017
  4. ↑ Arnst, John. "Why is there chatter in my Himalayan singing bowl?" Eurekalert. Acoustical Society of America, 5 Nov. 2015. Web. 21 Mar. 2017.
  5. ↑ White, Harvey E., and Donald H. White. Physics and Music: The Science of Musical Sound. Mineola: Dover Publications, Inc., 2014. Print.
  6. ↑ August, Brandon. "Dynamics of a Himalayan Singing Bowl." Acoustics.org. Rollins College, 15 May 2012. Web. 2 Feb. 2017
  7. ↑ August, Brandon. "Dynamics of a Himalayan Singing Bowl." Acoustics.org. Rollins College, 15 May 2012. Web. 2 Feb. 2017
  8. ↑ Arnst, John. "Why is there chatter in my Himalayan singing bowl?" Eurekalert. Acoustical Society of America, 5 Nov. 2015. Web. 21 Mar. 2017.
  9. ↑ August, Brandon. "Dynamics of a Himalayan Singing Bowl." Acoustics.org. Rollins College, 15 May 2012. Web. 2 Feb. 2017
  10. ↑ August, Brandon. "Dynamics of a Himalayan Singing Bowl." Acoustics.org. Rollins College, 15 May 2012. Web. 2 Feb. 2017
  11. ↑ August, Brandon. "Dynamics of a Himalayan Singing Bowl." Acoustics.org. Rollins College, 15 May 2012. Web. 2 Feb. 2017
  12. ↑ Heller, Eric J. Why You Hear What You Hear. Princeton: Princeton U Press, 2013. Print.
  13. ↑ Terwagne, Denis. "Tibetan Singing Bowls." Nonlinearity 24.8 (2011): 51-64. IOP Publishing Ltd & London Mathematical Society . Web. 2 Feb. 2017.
  14. ↑ Terwagne, Denis. "Tibetan Singing Bowls." Nonlinearity 24.8 (2011): 51-64. IOP Publishing Ltd & London Mathematical Society . Web. 2 Feb. 2017.
  15. ↑ Palmer, Jason. "How a Tibetan singing bowl is making waves in physics." BBC. N.p., 1 July 2011. Web. 21 Mar. 2017.
  16. ↑ Terwagne, Denis. "Tibetan Singing Bowls." Nonlinearity 24.8 (2011): 51-64. IOP Publishing Ltd & London Mathematical Society . Web. 2 Feb. 2017.
  17. ↑ White, Harvey E., and Donald H. White. Physics and Music: The Science of Musical Sound. Mineola: Dover Publications, Inc., 2014. Print.
  18. ↑ Terwagne, Denis. "Tibetan Singing Bowls." Nonlinearity 24.8 (2011): 51-64. IOP Publishing Ltd & London Mathematical Society . Web. 2 Feb. 2017.
  19. ↑ Terwagne, Denis. "Tibetan Singing Bowls." Nonlinearity 24.8 (2011): 51-64. IOP Publishing Ltd & London Mathematical Society . Web. 2 Feb. 2017.
  20. ↑ White, Harvey E., and Donald H. White. Physics and Music: The Science of Musical Sound. Mineola: Dover Publications, Inc., 2014. Print.
  21. ↑ Terwagne, Denis. "Tibetan Singing Bowls." Nonlinearity 24.8 (2011): 51-64. IOP Publishing Ltd & London Mathematical Society . Web. 2 Feb. 2017.
Retrieved from "https://wiki.ubc.ca/index.php?title=Course:PHYS341/Archive/2016wTerm2/TibetanSingingBowl&oldid=453971"