Organ Pipes

Fig. 1. Organ Pipes

A pipe organ is a keyboard instrument that produces sound by driving pressurized air through the pipes. The main components of an organ include an enclosed fan that generates pressured air, manuals of keyboards and pedalboard that initiate the organ's inner mechanism, and tuned pipes that resonate at the right pitch and radiate sound (Fig. 1).

Pipes are characterized as either flue or reed type. Within each type, the pipes come in different lengths and shapes. The variety of pipes allows an organ to produce a wide range of sounds with different timbres associated with orchestral instruments such as flute, oboe, trumpet, and strings. Moreover, an organ key can activate not only a single pipe one at a time but instead a combination of multiple pipes to enhance the fullness of a sound.

Organ Stops and Artificial Harmonics

Fig. 2. Organ stops are arranged to each side of the player.

Organ stops are electrical switches that control the combination of pipes (Fig. 2). When a stop is pulled out, the pressured air can travel through a particular set of pipes to produce sound. Although a pipe generally produces a series of natural harmonics on top of the fundamental frequency, additional pipes that generate artificial harmonics are often needed to produce a fuller sound. By pulling stops out and changing the combination of pipes, one can manipulate the overall dynamics and timbre of the sound.

The number printed on each stop indicates the length (in feet) of the longest pipe of the set associated with the stop and each set corresponds to a particular partial. For example, an 8-foot pipe corresponds to the fundamental frequency of 65 Hz, A2, a 4-foot pipe to the second partial (an octave above), a 2 2/3-foot pipe to the third partial (an octave and a fifth above), a 2-foot pipe to the fourth partial (two octaves above), and so on. In other words, longer pipes produce lower frequencies and shorter pipes produce higher frequencies. This phenomenon is consistent with the equation, velocity = frequency x wavelength, which governs that if the velocity of sound remains constant in all pipes, the wavelength of a pipe and its frequency are inversely proportional.

Practical Problem and Solution

In addition to upper partials, low notes are often needed to provide a strong bass for the harmony. While larger organs have 16-foot pipes that can produce notes an octave below the fundamental frequency, not all organs are built with 16-foot pipes due to the constraint of cost and space. Despite the lack of 16-foot pipes, however, one can still play a note an octave below the fundamental frequency using an 8-foot pipe if the pipe is closed at one end. This solution works because the wavelength of a closed pipe is twice the length of an open pipe of the same length.

Open vs. Closed End Pipes

Fig. 3. Open Pipe

Fig. 4. Closed-open Pipe

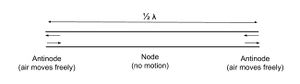
A cylindrical pipe with two open ends (Fig. 3) has velocity antinodes at both ends because air can move freely there when it is not blocked by a solid barrier. And between antinodes there is a velocity node midway because the air is preserved at rest at that point when air moves either towards the centre or away from the centre. Thus, the simplest vibration mode of an open pipe has two antinodes on the ends and one node in the middle. Since a complete wavelength of a cycle encompasses at least two antinodes and two nodes, the wavelength of an open pipe is twice as long as the length of the pipe.

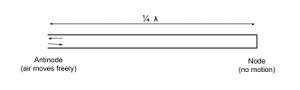
In contrast, a cylindrical closed-open pipe (Fig. 4) has only one antinode at its open end. The closed end is a velocity node because the air is blocked by the barrier at that point. Because a pair of antinode and node encompasses only a quarter of a wavelength, the wavelength of a closed-open pipe is four times the length of the pipe. Since the wavelength of a pipe and its frequency are inversely proportional, the frequency of a closed-open pipe is half the frequency (sounding an octave below) of an open pipe of the same length. Therefore, a closed-open 8-foot pipe can be used as a substitute of an open 16-foot pipe.

Overblowing Pipes as Contrasting Timbre

In some occasions, overblowing is used to create a contrasting timbre different from the normal timbre. Overblowing can be achieved by increasing the pressure of the air that goes through the pipes so that they resonate at other modes. Overblowing works better on open pipes than it does on closed pipes since open pipes have partials in the ratio of all integer numbers, 1:2:3:4 etc. while closed pipes have odd-numbered partials only, 1:3:5:7 etc. While the first mode of an open pipe has a wavelength of 2L (L = the length of the pipe), the second mode has a wavelength of L, which means the frequency of the second mode is an octave above that of the first mode. Therefore, if one wants to play a certain note with special timbre, he or she can play the note an octave below and with the right amount of pressure, the note would be brought up to the desired octave. For example, to produce A4 with special timbre, one should play A3 instead and adjust the air pressure so that the pipe resonates in its second mode.

Reference

1. Shannon, John R. Understanding the Pipe Organ. North Carolina: McFarland & Company, Inc., 2009.
2. Wood, Alexander. The Physics of Music. London: Chapman and Hall Ltd, 1975.
3. Closed and Open Ended Pipes. http://www.studyphysics.ca/newnotes/20/unit03_mechanicalwaves/chp141516_waves/lesson51.htm