Course:PHYS341/2022/Project28

A Soprano Recorder Dreaming of Venus

Introduction

As Elon Musk intends to colonize Mars, I thought that I needed to explore some other planet. Venus may be a poor choice, but here we are. And while spacesuit engineers are figuring out a way for my head to not explode on Venus, I could spend my time investigating a thing of equal value. Namely, if I were to play my little soprano recorder on Venus, what would happen to its sound wave properties?

I knew I was going to need some advanced materials and tools for this investigation. Thus I picked up some helium balloons from the dollar store. And then, I took the soprano recorder out of my drawer. As I already had the necessary software installed on my PC, I was good to go.

1) Background information

Changes in the speed of sound (Vsound) of a gaseous medium affects the wavelength and the frequency of a sound wave as per the equation v=f.𝜆. Although Vsound does not greatly differ on Earth due to relatively small changes in the properties of the medium, the atmosphere of Venus differs significantly in its properties compared to the surface atmosphere of Earth. Thus, we first need to see what such properties are, the effects they have on Vsound, and the significance of such properties in calculating the Vsound.

Note that speed of sound of gas (Vsound) depends only on the properties of the medium. It is not affected by the wave properties of the sound wave (frequency, amplitude, and wavelength) produced in that medium. The properties of a gaseous medium that affects Vsound of that medium are pressure and density.

Density (ρ):

Density (ρ) of a gaseous medium is the molecular mass (M) of the molecule it is composed of (or the aggregate of the masses of the molecules that it is composed of) divided by the its volume. Thus, a gaseous medium with a higher molecular mass (M) is more dense than a gaseous medium with a lower molecular mass (M).

The effects that density (ρ) has on Vsound is similar to the effect that mass/length of a stretched string has on its wave speed such that as density (ρ) increases, the Vsound decreases.

Pressure (P):

Pressure (P) of a gaseous medium is the force that air molecules exert on other air molecules (and other molecules/objects).

The effects that pressure (P) has on Vsound is similar to the effects that tension of a stretched string has on its wave speed such that as pressure (P) increases, Vsound increases.

Temperature (T) affects both density (ρ) and pressure (P). And the relation between pressure (P) and density (ρ) is that if temperature (T) was (regarded as being) invariable, then an increase in pressure (P) would amount to an increase in density (ρ) (and if ρ increased, P would increase). If pressure (P) was (regarded as being) invariable, then an increase in temperature (T) would amount to a decrease in density (ρ) (and if ρ increased, T would decrease).

Thus, both density (ρ) and pressure (P) vary with changes in temperature (T). However, when temperature (T) varies, they vary inversely and proportionally. Thus, in calculating the Vsound, it suffices to rely only on temperature (T).

Below is the equation for Vsound of gas:

v=√γRT/M

In this equation v stands for Vsound of gas, γ stands for adiabatic constant (different for different gases), R stands for the universal gas constant, T stands for temperature, and M stands for the molecular mass of gas.

For the purposes of this paper, we only need to note that given 1) γ and R are constant 2) we know the molecular mass for gas (for the gas that we are calculating Vsound of), and 3) we know the temperature (T) of the environment; we can figure out the speed of sound for that gas. In the following section, I will use this equation to calculate the Vspeed of a given gas in a given environment.

2) Vsound - Air, Carbon Dioxide, and Helium:

The gas composition of the surface-atmosphere of Earth is roughly 78.09 % nitrogen, 20.95 % oxygen, and 0.93 % argon). At a temperature of  15 °C - which amounts to around 288 Kelvin - is calculated to be 343 m/s.

The surface-atmosphere of Venus has almost an entirely different gas composition compared to earth with it being roughly constituted of only 3.5 % nitrogen and of 96 % carbon dioxide. For the purposes of this paper, I will regard its composition as being 100 % carbon dioxide, which -  as we will see - does not greatly affect the calculation of the speed of sound.

Gas composition is not the only property of their atmospheres that is strikingly different. While the average temperature of the surface-atmosphere of Earth is roughly around 15°C (Footnote: 13.9 to be exact), the average temperature of the surface-atmosphere of Venus is roughly around 464°C. Yes, I know that both my soprano recorder and I will burn down, but I kindly ask the reader to ignore this unfortunate fact. Remember the formula above for the Vsound of a gas? Note that regarding the surface-atmosphere of Venus, we know that temperature (T) is 464°C and the gas (carbon dioxide), and thus its molecular mass (M). And given that γ and R are constant, all values necessary to calculate the Vsound on the surface-atmosphere of Venus is available. First, let’s make sure we know the proper values of the constants and the variables, as well as their appropriate units.

v=√γRT/M

Adiabatic constant (γ) for CO2 at 400°C is 1.235 γ (for our purposes, this is close enough to 464°C). But note that this equation uses the Kelvin temperature scale, and 464 °C amounts to 737.15 Kelvin (K). The universal gas constant (R) is 8.314 J/mol. The molecular mass of CO2 is 0.04401 kg/mol. The average temperature of the atmosphere of Venus is 737.15 K.

v=√γRT/M

v=√(1.235γ)(8.314J/mol)(737.15K)/0.04401kg/mol

v=√(7,568.9)/0.04401

v=414.7m/s

Needless to say, the Vsound on the surface-atmosphere of Venus has been calculated before. Nevertheless, the calculation in this paper comes very close to the already calculated value of 410m/s.

Thus, the Vsound on the surface-atmosphere of Venus (410m/s) is higher than that of Earth (343m/s). Thus if I put my finger on the first fret of the high E on my guitar as standing on Venus, the frequency of the sound wave would not be any different than if I were to play it on Earth. This is because on string instruments, sound waves are transmitted via a medium (its strings) other than the surrounding gas molecules. I would then observe different wavelengths, and not different frequencies when I position my finger on the guitar identically in Venus and in Earth. Specifically, given that the speed of sound on the surface atmosphere of Venus is higher than that of Earth, I would observe higher wavelengths on Venus when I position my finger identically within the two atmospheres. And this reasoning holds because of the equation below,

v=f.𝜆

However, I will use a recorder, a type of wind instrument, as my object of analysis in this investigation. This is because 1) I took all that time to calculate the Vsound, 2) I only have a soprano recorder at home, and more importantly so 3) Unless one altered the instrument itself (such that the length of the tube is has changed), the allowed wavelengths would not differ between two given environments. Thus, as per the equation above, it must be the frequencies that changes in positioning my fingers identically in both atmospheres. And, it is more exciting to observe changes in frequencies rather than in wavelengths! Then, let’s investigate what would happen to the properties of the sound wave if I were to play my soprano recorder on Venus.

To play a note (some Hz X) on my recorder, I blow air (the gas composition of the surface-atmosphere on earth) into it. If I were to inhale some other gas and blow that into the recorder, then the wave speed would be different. Because regarding wind instrument, wave speed just is the Vsound of the surrounding gas composition. This is because sound waves (which would be standing waves in their form) are transmitted via disturbance of the gas molecules. Then, Vsound would change respectively to the properties of the surrounding gas (given that temperature (T) and Pressure (P) of the environment are constant).

As stated previously, Venus is mostly composed of carbon dioxide. And this fact exposes two problems. First, I cannot (yet) go to Venus; and second, I should not inhale carbon dioxide from my soda stream (or from any source for that matter). But, there is a (questionably) inhalable gas that would produce a higher Vsound than that of the gas composition of Earth’s surface-atmosphere. And being able to experiment with a higher Vsound is sufficient to make predictions about the Vsound in Venus. By investigating the surface-atmosphere of Venus, we figured out that it has a comparatively higher Vsound. And as the Vsound is the property that induces the kinds of effects that we want to examine on the properties of a sound wave, we could use any Vsound that is higher than Vsound of air. Helium is a great choice of gas for this investigation because it has a higher Vsound than air. Plus, I can buy a helium balloon from the near-by grocery store and inhale it without major medical consequences!

Referring back to the formula of Vsound of gas,

v=√γRT/M

Figure 1. The recorder is a tube with both ends open. The purple dots represent the holes that were blocked in producing the note. The mouthpiece is one end and the first hole available is the other end of the tube. The length from the mouthpiece to the first hole available is 18.9cm/0.189cm.

Helium has a particular adiabatic constant (γ) at some temperature T and its molecular mass (M) is 0,004kg/mol. In comparing it to the molecular mass (M) of air (0.029kg/mol), we can mathematically observe that the density of helium is lower than the density of air. Since we are conducting our experiment on earth, I will take the value of temperature (T) to be the average temperature of the surface atmosphere of earth which is 15 °C/288 K. And at 288K, the adiabatic constant (γ) for helium is 1.67γ. Thus, the vSound of helium on the surface-atmosphere of Earth would be,

v=√γRT/M

v=√(1.67γ)(8.314J/mol)(288K)/(0.004kg/mol)

v=999m/s

Effects of wave speed (Vsound) on the properties of a sound wave

Vsound in helium is higher than the Vsound on the surface-atmosphere of Venus (carbon dioxide) but this does not pose an issue. Because all we need is a Vsound that is higher than the Vsound in air. In the following section, I will demonstrate my frequency calculations and compare them to the results obtained via recordings.

Calculations of allowed wavelengths and frequencies

I calculated fundamental frequency and its harmonics using the following information:

A) With the upper two holes of the recorder closed (Figure 1), the length of the recorder from the mouthpiece until the first open whole - which would act as the second end of the tube - amounts to 18.9cm/0.189m.

B) A recorder is an open tube, with antinodes on both ends. Figure 5 and 6 demonstrate 1) the standing waves and calculations of the wavelengths up until the 4th harmonic, 2) the calculated frequencies of soundwaves produced in air and helium.

1. 

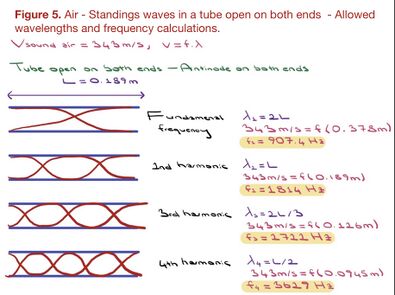
   Figure 5. Estimated fundamental frequency and harmonics calculation based on allowed wavelengths in a 18.9cm recorder and Vsound in air.

Sound wave properties of sounds produced in air vs. in helium

I played the recorder with two upper holes closed 1) with inhaling helium and 2) without inhaling helium. I recorded the sounds produced and the software transcribed the time graph to the frequency spectrum via the Fourier transform.

Figures 2 and 3 demonstrate that a 18.9cm recorder produces sounds with different frequencies (Hz) depending on the gas composition of the surrounding air (helium or air). Further, it can be observed that the amplitude of the harmonics of their distinct fundamental frequencies also differed (Figure 2 and 4). Figure 4 demonstrates that the third harmonic of the sound wave produced in helium has a higher a amplitude than the second harmonic; while the opposite is holds for the sound wave produced in air. And while the sound wave produced when I could not properly inhale the helium produced frequencies near identical to the produced frequencies in air, it can be observed that different harmonics of the same fundamental frequency were emphasized (figure 2 and 4). Thus, the sound waves differed in timbre even when they did not differ in frequency.

Figure 6. Estimated fundamental frequency and harmonics calculation based on allowed wavelengths in a 18.9cm recorder and Vsound of in helium.

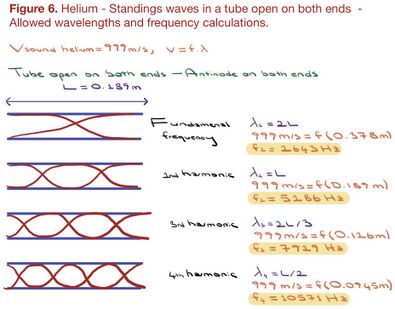
The calculated frequencies of sound waves produced in air ended up being near-identical to the values observed from the recordings (figure 5 and 2). Note that the calculations of the sound wave’s fundamental frequency and harmonics in helium did not correspond to the recordings (figures 3 and 6). Further, the fundamental frequency produced in helium (2643 Hz) must have been 2.9 times higher than the frequencies produced in air (907.4 Hz) (figure 3 and 6). But the observed frequencies from recordings demonstrate only a ratio of 1.37. However, the issue here is not the calculations. Rather, we must consider the fact that the experiment was produced in highly non-ideal conditions. I could not ensure that there were no air molecules in the helium balloons, to begin with. And given that the amount of helium inhaled was not known, it is unavoidable that I blow air molecules along with the helium molecules. With air molecules having lower molecular mass (M), helium mixed with air would amount to a lower speed of sound than Vsound in helium. And a lower speed of sound would amount to a lower frequency. If the experiment could have been produced in perfectly ideal conditions, then the calculations predicted would have been observed in the spectrum graphs of recorded sounds.

To conclude

This exploration demonstrated that a frequency produced with a particular length of the recorder (tube) would be different on Venus compared to Earth. Further, one can expect to observe a differing emphasis - amplitude values - of the harmonics of a fundamental frequency between the two atmospheres. Although there are clearly many factors regarding an atmosphere this exploration could not account for, I hope I could nevertheless make some reasonable predictions regarding the relations between the properties of an environment and the properties of sound waves with the limited information I had.