Course:MATH110/Archive/2010-2011/003/Teams/Zug/Homework 12
Starting with the function
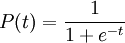
Your goal is to modify the function so that we can use it to model a real-life problem. We want to be able to control the following things:
Change the height of the horizontal asymptote on the right, we'll denote it by K. Change the y intercept to any number between 0 and K
To change the height of the horizontal asymptote, we need to change the numerator and the denominator. The horizontal asymptote depends on the numerator, and the part of the denominator independent of e. In this case 1 and 1. If t goes to infinity, p(t) = 1/1 = 1, therefore, in this case, the horizontal asymptote will be 1. When the equation is changed to: 5/(2.5 + e^-t), the asymptote is 2.
The y intercept in this equation is always 1/2 of K
For example:
For 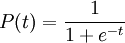the y intercept is 0.5, in the case of
5/(2.5 + e^-t), it is 1.
So the vertical asymptote is always 1/2 of the horizontal asymptote at the right.
The slope of the curved part depends on the constant multiplied to t in the power of e.
For example: the slope of the curved part of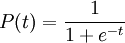
will be steeper than the slope of the curved part of 1/(1 + e^(-3t))
and the slope of the curved part for
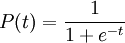
will be steeper than that of P(t) = 1/(1 + e^-0.5t)
The function may be used to model the economic growth for developing countries. It is often seen that underdeveloped countries have a higher rate of economic growth than developed countries. When a country reaches its capacity level of output, the rate of economic growth decreases. For convenience let us assume economic growth is measured by the GDP of the country. Therefore, the P(t) axis shows the GDP in millions of dollars, and the t axis denote time. If the capacity of the economy’s GDP is 40 million dollars, and at t=0 the GDP is 20, and the rate of increase is such that the constant multiplied with t is 0.05. The function should be
P(t) = 40/(1 + e^-0.05t)
The capacity level of GDP is 40 million. 95% of that is, 38 million. Therefore we can say that:
38 = 40/(1 + e^-0.05t)
38 + 38 e^-0.05t = 40
38 e^-0.05t =2
e^-0.05t = 2/38
e^0.05t = 19
ln e^-0.05t = ln 1/19
-0.05t = ln(1/19)
t is approximately 58.888
Therefore in 58.8 years the economy will reach 95% of its capacity level of GDP