Course:MATH110/Archive/2010-2011/003/Teams/Vaud/Homework 13

Homework 13

Decibels:

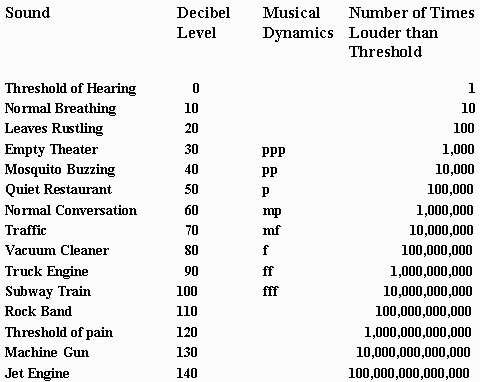
A decibel (dB) is a logarithmic unit that compares sound level. Usually it refers to the intensity or strength of a sound. It is equal to one tenth of a bel, (symbolized as B, and named after Alexander Graham Bell) a name which nobody really uses at all. Because there is such a wide range of sound the human ear can detect, decibels operate on a logarithmic scale. The decibel scale can quickly tell us in what range of sound we're dealing with. If a sound is twice as loud as another, then it is 10 dB louder. Sound still exists at 0 dB because it is a way of comparing sounds and it's all relative. The human ear is so sensitive that it can pick up sounds at the end of the sonic spectrum, and it can pick up noises that are thousands of times less intense and powerful than others.

Our ears operate sort of like logarithmic scale when detecting loudness. Sound intensity, I (in Watts/square metre), is how fast sound waves push energy through an area. The logarithmic scale of sound intensity is called the intensity level where one bel represents a difference between two intensities $I_{0},I_{1}$. This can be expressed as:

Sound/Intensity level $=10log_{10}{\frac {I_{1}}{I_{0}}}*dB$

For example, the difference in sound intensity between $10^{-8}watts/m^{2}$ and $10^{-4}watts/m^{2}$ can be found in decibels using the above equation.

ΔI=$10log{\frac {10^{-4}watts/m^{2}}{10^{-12}watts/m^{2}}})-10log({\frac {10^{-8}watts/m^{2}}{10^{-12}watts/m^{2}}})$

=40dB

Increasing the sound intensity by:

• 10 raises its level by 10db
• 100 raises its level by 20dB
• 1,000 raises its level by 30 dB
• 10,000 raises its level by 40dB

This site can give you an idea of how common sounds around us are measured in decibels. It will also tell you how much sound intensity the human ear can take and what effects prolonged exposure to loud noises can have : http://www.gcaudio.com/resources/howtos/loudness.html

Our ears can handle at the loudest $1watt/m^{2}$ and at the quietest $10^{-2}watts/m^{2}$. 0 dB is recognized as the threshold of hearing and is used a reference all over the world when measuring decibels.