Course:MATH110/Archive/2010-2011/003/Teams/Valais/Homework 13

Logarithmic Scale

LOGARITHMIC SCALE

A Logarithmic Scale can be defined as the scale on which actual distances from the origin are proportional to the logarithms of the corresponding scale numbers or scale of measurement that uses the logarithm of a physical quantity instead of the quantity itself A log scale makes it more helpful and manageable to compare a large range of values. The logarithmic scale can be helpful when the data covers a large range of values – the logarithm reduces this to a more manageable range. For example, a graph's axis is labelled 10, 100, 1000, and 100000 instead of 1, 2, 3 and 4. This is a common and useful measurement scale that is used for measuring entropy, pH, acoustic power, entropy and sesimic energy among many other things. We will investigate how the Richter Magnitude Scale works on a logarithm scale.

Richter Magnitude Scale

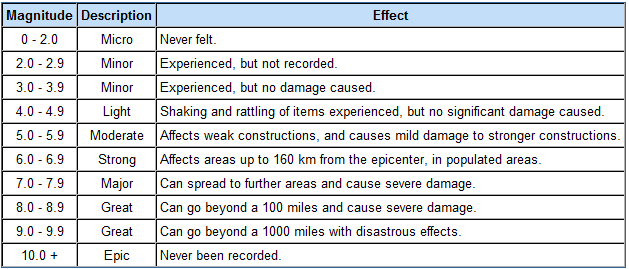
Invented by Charles Richter in 1935, the Richter Scale or the Local Magnitude Scale (ML) measures the magnitude of earthquakes. More precisely, the Richter scale is a measure of ground movement at the epicenter of an earthquake which can be in turn be used to determine the sesimic energy released by an earthquake.

The Richter Scale is a logarithmic scale; thus, each order of magnitude increase is tenfold. This means that each number increase on the Richter scale indicates an intensity ten times stronger. The range of the Richter scale is between 0 and 10. An earthquake can measure above 10.0, which is then called an epic earthquake.

An earthquake of magnitude 6 is ten times stronger than an earthquake of magnitude 5. An earthquake of magnitude 7 is 10 x 10 = 100 times stronger than an earthquake of magnitude 5. An earthquake of magnitude 8 is 10 x 10 x 10 = 1000 times stronger than an earthquake of magnitude 5. In terms of energy, a whole number change approximately corresponds to 31 times more or less energy being released .

Comparing Earthquakes

How does a magnitude 5 quake compare to a magnitude 2 earthquake? The increase in magnitude is 5-2 or 3. $10^{3}=1000$; thus the ground movement of a magnitude 5 quake is 1000 times greater than a magnitude 2 quake. How does a magnitude 7 quake compare to a magnitude 1 earthquake? The increase in magnitude is 7-1 or 6. $10^{6}=1000000$ thus the ground movement of a magnitude 7 quake is one million times greater than a magnitude 1 quake. As illustrated in the examples above, there is are large differences between the impact of earthquakes because of the Richter scale being a logarithmic scale.

---

The Richter magnitude of an earthquake is determined from the logarithm of the amplitude of waves recorded by seismographs. </ref> or scale of measurement that uses the logarithm of a physical quantity instead of the quantity itself The original formula is:

Earthquake intensity is measured by the Richter scale. The formula for the Richter rating of a given quake is given by "R= log[ I ÷ I0]"

• I0 is the "threshold quake", or movement that can barely be detected and I, the intensity, is given in terms of multiples of that threshold intensity.
• Suppose a seismograph measures that the I= 989I0.
  • To determine the magnitude of the earthquake, the intensity to a Richter rating by evaluating the Richter function at I= 98910:R = log[I ÷ I0 ]=log[ 98910 ÷ I0] =log[989]=2.99519629... or about 3 on the Richter Scale, which turns out to be a minor earthquake.

---

---

References: