Course:MATH110/Archive/2010-2011/003/Teams/Schwytz/Homework 13
Pick one of the topic offered below and then explain in your own words what it means that these concepts work on a logarithmic scale.
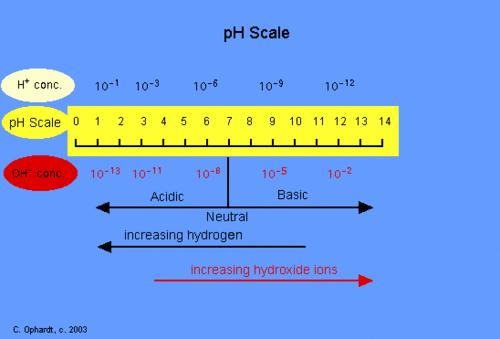
- Our team has decided to look at PH and how it works on a logarithmic scale.
From previous knowledge we know that the pH scale is a range of acids to bases. The scale ranges from 0 to 14, with 0 being the most acidic and 14 being the most basic.
According to: http://www.sciencebuddies.org/science-fair-projects/project_ideas/Chem_AcidsBasespHScale.shtml
An acid can be defined as: a substance that has a very high concentration of hydrogen ions. From this we know that when an acid is dissolved in water, the balance between hydrogen ions and hydroxyl ions is shifted in the solution. Having more hydrogen ions=acidic solution.
A base can be defined as: a substance that accepts hydrogen ions. From this we know that when a base is dissolved in water, the balance between hydrogen ions and hydroxyl ions shifts the opposite way. Having more hydroxyl ions=basic solution or alkaline.
Acidity and alkalinity are measured on a logarithmic scale called the pH scale.
From our research we found that one of the reasons the pH scale uses a logarithmic scale is because if we take a really strong acidic solution, it can have one hundred million million (100,000,000,000,000) times more hydrogen ions than a strongly basic solution and a strongly basic solution can have 100,000,000,000,000 times more hydroxide ions than a strongly acidic solution the hydrogen ion and hydroxide ion concentrations these solutions can vary over that entire range.
The logarithmic scale shows the following pattern: Each single unit change in the pH scale corresponds to a change in hydrogen ion concentration of ten times!
So the benefit of using a logarithmic scale is that you don't have to write all the zeros.
From further research on http://www.elmhurst.edu/~chm/vchembook/184ph.html we found examples to prove this:
- A pH reading of 4 is ten times more acidic than a pH of 5 and 100 times (10 times 10) more acidic than a pH of 6
- A pH reading of 10 is ten times more basic than a pH of 9 and 100 times (10 times 10) more baisc than a pH of 8
The following equation is used to calculate the pH or hydrogen ion concentration using logarithms:(found on http://www.elmhurst.edu/~chm/vchembook/184ph.html)
- pH is defined as follows: pH = -log10[H+]
This means that if you have a hydrogen ion [H+] concentrations of 0.1M (where M is the concentration in moles per liter)the equation would be used as seen below:
pH = - log10(0.1)
pH = - (-1)
pH = 1 , [0.1 = 10^-1, so log10(0.1) = -1]
Sample Problem:
- if an acid has a hydrogen ion concentration [H+] of 0.0001 M, find the pH.
In order to solve this we can first convert the number to exponential notation, find the log, then solve the pH equation as shown below:
[H+] 0.0001 M = 10^-4; log 10^-4= -4
pH = -log[H+]
pH = -log(10^-4)
pH = -(-4)
pH = +4
The purpose of the negative sign in the log definition is to give a positive pH value.
Example is taken from: http://www.elmhurst.edu/~chm/vchembook/184ph.html