Course:MATH110/Archive/2010-2011/003/Notes/Limits at a point (precise definition)

What is a limit?

We use limits to understand the behaviour of functions in the neighbourhood of some specific points. For example, consider the following example.

Example 1

Consider the functions given by

$f(x)=\frac{1}{2-x}g(x)=\frac{x^2+x-6}{x-2}$

which is defined everywhere except at $x=2$. We're very interested in knowing what happens to the function as it gets closer to that specific value. We could first try to plot the function near that point. If we do this for values that are getting closer to 2 from below, we get the following data:

$x$	$1$	$1.2$	$1.4$	$1.6$	$1.7$	$1.8$	$1.85$	$1.90$	$1.95$	$1.96$	$1.97$	$1.98$	$1.99$
$f(x)$	$1$	$1.25$	$1.67$	$2.5$	$3.33$	$5$	$6.67$	$10$	$20$	$25$	$33.33$	$50$	$100$
$g(x)$	$4$	$4.2$	$4.4$	$4.6$	$4.7$	$4.8$	$4.85$	$4.9$	$4.95$	$4.96$	$4.97$	$4.98$	$4.99$

It seems that the function $f$ is getting bigger and bigger as the values gets closer to $2$ (from below); whereas the function $g$ seems to get closer and closer to the number $5$. But how to make sure of that intuition?

Informally, we say that the number $L$ is the limit of the function $f$ as $x$ approaches the point $a$ if the values of $f(x)$ become arbitrarily close to the number $L$ for values of $x$ sufficiently close to $a$.

We should be careful to see if we're approaching the function from the left or from the right, as it might yield different results. The key issue and motivation behind this more precise definition is to make sense of the arbitrarily close and sufficiently close as written above. So, say you want to check that function $g$ as above does admit $5$ as its limit as $x$ approaches $2$; then being arbitrarily close means that the difference between $g(x)$ and $5$ should become as small as I want if I'm close enough to $2$. We'll write this:

If for every positive number $ϵ$ (think of it as being small, it's the one encoding the arbitrarily close) we can find another positive number $\delta$ such that

$|g(x)-5|<ϵ$

for every $x$ between $2-\delta$ and $2$, then we'll agree to say that the limit of the function $g$ as $x$approaches $2$ is $5$. Since we only look at values of $x$ that are less than $2$, this is actually a limit on the left. For the limit on the right, with values of $x$ just above $2$, we would look at values of $x$ between $2$ and $2+\delta$.

For instance, if we chose the value $ϵ=0.1$, we can find that $\delta =0.1$ works as all the values of $x$ between $1.9$ and $2$ (not included) have their $f(x)$ values no further away from $5$ than $0.1$.

Precise definitions

We're ready now to write this more formally and more precisely. Let $f$ be a function, call the number that is the limit $L$ and let the point at which we're looking be $a$.

• We'll say that $f$ admits the number $L$ as its limit on the left as $x$ approaches $a$ if for every positive number $ϵ$, there exists a positive number $\delta$ (which might change as you change the value of $ϵ$) such that:

$|f(x)-L|<ϵ$

for all the values of $x$ that are between $a-\delta$ and $a$ (in other words: $a-\delta <x<a$). And we'll write this as:

$\underset{x\to a^{-}}{\lim }f(x)=L$

• We'll say $L$ is the limit on the right as $x$ approaches $a$ if for every positive number $ϵ$, there exists a positive number $\delta$ (which might change as you change the value of $ϵ$) such that:

$|f(x)-L|<ϵ$

for all the values of $x$ that are between $a$ and $a+\delta$ (in other words: $a<x<a+\delta$). And we'll write this as:

$\underset{x\to a^{+}}{\lim }f(x)=L$

• Finally, we'll say that the number $L$ is the limit as $x$ approaches $a$ if it is both the limit on the left and on the right.

Example 2 (a function that admits a limit)

Let's get back to the second function of the first example above and test our definitions.

That function should at least admit $5$ as a limit on the left, according to the data shown in the table. How do we show this? Let's pick a small positive value (you think of one, I think of one) we'll call it $ϵ$. We want to make sure the values of $g(x)$ get very close to $5$, so we have to look at

$|g(x)-5|=|\frac{x^2+x-6}{x-2}-5|$ $=|\frac{x^2+x-6}{x-2}-\frac{5(x-2)}{x-2}|$ $=\left|\frac{x^2-4x+4}{x-2}\right|$ $=\left|\frac{(x-2{)}^2}{x-2}\right|$ $=|x-2|$

For values of $x$ less than $2$, the number $x-2$ will be negative, hence applying the absolute value yields:

$|x-2|=-(x-2)=2-x$

So we found that

$|g(x)-5|<\epsilon$

is equivalent to

$2-x<\epsilon$

(for values of $x$ less than $2$ only) or in other words:

$2-\epsilon <x<2$

This shows that we can let $\delta$ be exactly the same as $ϵ$ and this proves that

$\underset{x\to 2^{-}}{\lim }g(x)=5$

The fact that $\delta =ϵ$ here can be observed from the above table. Indeed, we can see there that in order to be say $0.01$ close to the value $5$, we need $x$ to be $0.01$ close to $2$. The first $0.01$ is the $ϵ$ and the second one is the $\delta$.

Now in the case of the limit on the right, that is, for values of $x$ larger than $2$, we can reuse a lot of our work. We still have that:

$|g(x)-5|=|x-2|$

but since now $x$ values are larger than $2$ we have that

$|x-2|=x-2$

Hence, we find that:

$|g(x)-5|<\epsilon ⟺|x-2|<\epsilon ⟺2<x<2+\epsilon$

This means that once again, we can let $\delta =ϵ$ and the above shows that

$\underset{x\to 2^{+}}{\lim }g(x)=5$

Since both limits on the left and on the right are the same, we can conclude that the limit of the function $g$ as it approaches $2$ is 5.

We can observe this if we plot the function:

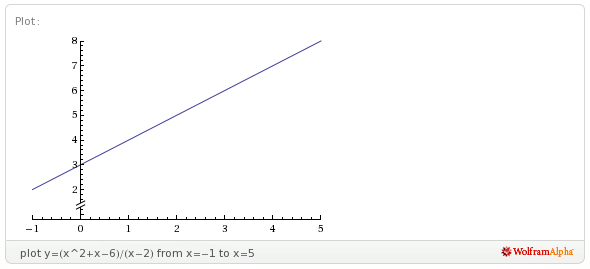
As you can see, it is as if the function takes the value $5$ at the point $x=2$ (the hole is so small, you can't see it). It is also interesting to see the graph looks like a straight line. Is it really?

Example 3 (a function that does not admit a limit)

Let's now study function $f$ from example 1. It seems that on the left, the functions grows to infinity as it approaches $2$. Can we show this?

We could show for example that whatever value $M$ you pick, the values of $f(x)$ will become larger than that number if we're close enough to $2$. So, we want $f(x)>M$ for any value $M$ (that could be very big). We can see that:

$f(x)>M⟺\frac{1}{2-x}>M⟺1>M(2-x)$

if $2-x>0$ (otherwise, the inequality flips sides), but that's exactly when $x<2$, so we're good since we said we were looking at what's going on on the left. Let's continue:

Failed to parse (syntax error): {\displaystyle 1 > M(2-x) \iff 1 >2M - Mx } $⟺Mx>2M-1⟺x>\frac{2M-1}{M}=2-\frac{1}{M}$

again, we can divide by $M$ without flipping the sides of the inequality if we assume that $M$ is positive.

So what does this say? It says for example that if you want Failed to parse (syntax error): {\displaystyle f(x) > 1000} , then simply let

$x>2-\frac{1}{1000}=1.999$

In other words, we can precisely say how close to $2$ you have to take your values of $x$ to have the values of $f(x)$ be as large as you want. This shows that the function $f$ does not admit a limit as it approaches $2$.

Now, what about the other side? What if we take values of $x$ larger than 2? We could see that the values of the functions were getting larger because we were dividing $1$ by a very small and positive number. If now $x$ is larger than $2$, then the value of $2-x$ will be a small but negative number. So we get the same effect of getting a large number because we're dividing by a small number, but this time the whole thing becomes negative. Can we check that intuition more precisely?

Say now that $M$ is a very large negative number (think: $M=-1000$). We claim the function will become even more negative that this if we get close enough to $2$. So we want to know when is $f(x)<M$. We get:

$f(x)<M⟺\frac{1}{2-x}<M⟺1>M(2-x)$

(since $2-x$ is negative, multiplying by this flips the inequality). And if we continue we get that:

$1>M(2-x)⟺1>2M-Mx⟺Mx>2M-1$ $⟺x<\frac{2M-1}{M}=2-\frac{1}{M}$

(again, remember that $M$ is a negative number, so dividing by it flips the inequalities again).

So what does this say? It says for example that if you want Failed to parse (syntax error): {\displaystyle f(x) < -1000} , then simply let

$x<2-\frac{1}{-1000}=2.001$

In other words, the closer we get to $2$ (from the right), the more the values of $f(x)$ will get closer to $-\mathrm{\infty }$. This clearly shows that the function $f$ does not admit a limit on the right either.

Let's check all this by looking at the graph of the function:

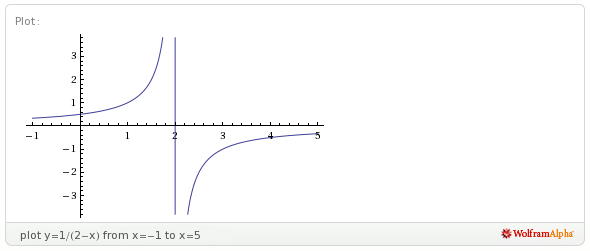
We can observe that at $x=2$ (the vertical blue line) the function explodes to positive infinity on the left and negative infinity on the right. We call this behaviour a vertical asymptote.

Related examples and problems

This all connects very well in the textbook with section 2.2. Do problems 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 15, 16, 23, 24, 25, 30, 31, 32. Remember you're by far not the only one working on these problems, if you're stuck or would like to discuss your work, use the wiki. You could ask your group or everyone using the Math Forum page.