Course:MATH110/Archive/2010-2011/003/Math Forum/Webwork A4

Q5

I have a question about Question 5 on WebWorks:

Find the equations of the horizontal asymptotes and the vertical asymptotes of . If there are no asymptotes of a given type, enter 'NONE'. If there is more than one asymptote of a given type, give a comma seperated list (i.e.: 1, 2,...).

I have found the horizontal asymptote and it is correct.

But the vertical asymptote is wrong, even though I've checked it through subbing it back into the equation and graphing.

Does anyone know how to solve it or if they have the same problem? EllenTsang 23:31, 17 October 2010 (UTC)

Hi Ellen,

The vertical asymptote occurs when $3x^{2}+3x-6=0$ . Try factoring this and see what you get! CharlyHuxford

Q12

Does anyone have an idea on how to do Question 12 on the Webworks:

Find the values of c and d that make the following function continuos for all x.

f(x)=9x if x<1

cx^2+d if 1<x<2

3x if x>2

SeanNugentSean Nugent

Because they want the function to be continuous your limit when approaching from the left must equal your limit when approaching from the right side.

lim f(x) 9x = lim f(x) cx^2 +d and lim f(x) cx^2 + d = lim f(x) 3x

The limit for the first part should be equal to 1 if it is to be made continuous, as this is where the discontinuity is. You can substitute 1 into the spot of x and isolate either d or c. The limit for the next part is 2 (once again where the discontinuity is and if they want it continuous....), solve for the opposite variable.

Following the rules of continuity the limit when approaching from the left must equal the limit when approaching from the right, so you can put your two equations together and solve for c or d and than substitute in to solve for the other.

so 9(1) = c(1)^2 + d --> 9 = c + d --> 9 - c = d. Do the same to the other side and solve and than substitute.

Hopefully that helps!

StephanieUrness

Q20

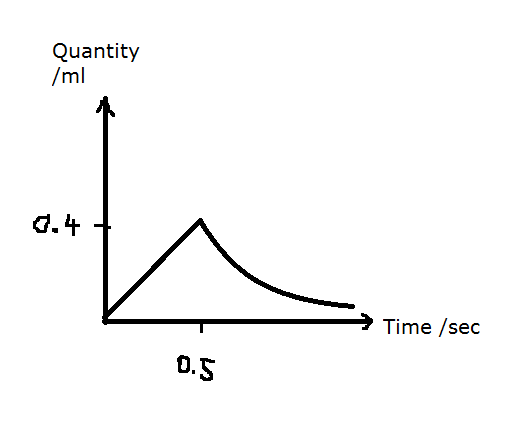
A 0.4 ml dose of a drug is injected into a patient steadily for 0.5 seconds. At the end of this time, the quantity, $Q$, of the drug in the body starts to decay exponentially at a continuous rate of 0.35 percent per second. Using formulas, express $Q$ as a continuous function of time, $t$, in seconds.

I drew a diagram:

And I got:

$Q(t)={\tfrac {4}{5}}\ t$ if $0\leq t\leq 0.5$

I am trying to find what is Q(t) for when t is after 0.5:

$Q(t)=$_______? if $0.5\leq t\leq \infty$

I tried using the decay formula, $a(1-r)^{t}$.

And I put $0.4(1-0.35)^{(}t-0.5)$ ...as in, to the power of $t-0.5$, I don't know why it doesnt show clearly here.

But it didn't work.

Does anyone know how to do this? EllenTsang

---

Oh, wow. I realized it's 0.0035, not 0.35.

So it's $0.4(1-0.0035)^{(}t-0.5)$.

I hope nobody else spent ages on this question because of the same thing, haha! EllenTsang