Course:MATH110/Archive/2010-2011/003/Groups/Group 17/Basic Skills Project

The Pythagorean Theorem

What Is It?

A geometric visualization of the Pythagorean Theorem

History:

The theory was originally developed by a man named Pythagoras, who was born in the late 6th century B.C. on the island of Samos, Greece. He proved that for any right angle triangle, the two shorter sides squared and added together exactly equal the square of the longest side. This can be shown mathematically as:

$a^{2}+b^{2}=c^{2}$

Pythagorean Basics:

The theorem only works for triangles, specifically those with a right (90 degree) angle.

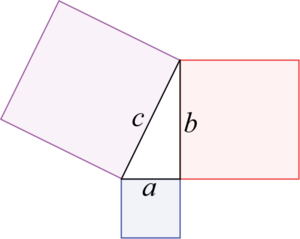
This image gives a visual example of how the Pythagorean theorem looks. The larger square has each side equal to the length of the hypotenuse (longest side) of the triangle. The two smaller squares are formed from the other two lengths on the triangle.

The theory, at it's most basic, states that the area of the largest square is equal to the combined areas of the two smaller squares. Since the area of a square is given by multiplying the length of a side by itself, we can label the sides above as shown, and bring ourselves right back to the mathematical formula! $a^{2}+b^{2}=c^{2}$

The following video shows a basic use of the theorem.

For an interesting visual example, watch the following video. It shows that the water from the large square, formed by the hypotenuse, fills the smaller squares formed by the other two sides. Note that though this is an interesting visualization of the theorem, it is not actually a concrete proof, simply an interesting visual demonstration.

How Do We Know It's True?

An example of a proof of the Pythagorean Theorem

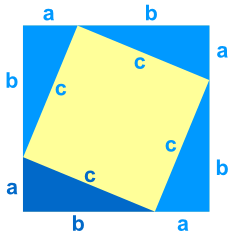
There are many proofs of the theorem. One of the most straightforward is the following:

Take four right-angled triangles and connect them into a square as shown, so that they hypotenuses form an inner square as follows:

We can see that the length of each side of the outer square is $a+b$, and that the area must be $(a+b)^{2}$.

The pieces of the square are the inner square and our four triangles.

The area of each triangle can be given as ${\tfrac {1}{2}}ab$.

Meanwhile, the inner square has side length of $c$, and area of $c^{2}$.

From this, we can see that:

$(a+b)^{2}=2ab+c^{2}$

Expanding, we see that:

$\ a^{2}+2ab+b^{2}=2ab+c^{2}$

Balance the equation by subtracting $2ab$ to get:

$a^{2}+b^{2}=c^{2}$

This is, of course, the formula for the theorem!

What Can We Do With It?

Once you know the fundamentals of Pythagorean Theorem you can broaden the range of questions that you do and you can solve much more difficult questions with multiple steps involved.

One example of a real-life application of the Pythagorean theorem would be figuring out the necessary height of an object. Lets suppose you have a 15 meter high wall. You want to find out how long a ladder has to be if it is 5 meters from the base of the wall. Implementing the Pythagorean theorem one is able to solve this issue with little to no issues. By simply substituting 5 and 15 for a and b (in the formula) we can obtain the result which will give us the necessary height of the ladder.

Therefore:

$5^{2}+15^{2}=250$

${\sqrt {250}}=15.8m$

15.8 meters is the exact height the ladder must be to fit the given parameters of the wall.

As another example, let’s assume two friends Fred and Matt want to meet at a specific point, say a shopping mall. Fred is 8 km North of the mall and Matt is 7 km East of the mall (forming a right angle from the mall.) How do we find the distance between the two of them? By using the Pythagorean theorem we are able to determine the distance between them.

Let's call $a$ the distance between the mall and Fred and $b$ the distance between Matt and the mall. This means that the distance between the two friends can be labelled $c$. We can input these values into our formula:

$5^{2}+7^{2}=c^{2}$

So, $c={\sqrt {25+49}}$

${\sqrt {74}}=8.6km$

So we now know that Fred and Matt are 8.6 km from each other.

Other common questions could be based on discovering how much time you save by cutting across a field, calculating the length of a shadow cast by a building, or even calculating the height of a building based on the shadow. It can be used to find the length between the corners of a ceiling or floor while laying tiles.

A couple examples of other things you could use the theorem for would be computing Euclidean distance in various coordinate systems, Pythagorean trigonometric identities, along with complex arithmetic and various other questions. The following pdf attachment contains many problems of increasing complexity.

Follow this link for further examples.

They Pythagorean Theorem can even be applied in video games! As awkward as this game may be, it shows the integration of mathematics into the gaming world.

What Does This Have To Do With the Trigonometric Circle?

Given that the radius of a trigonometric circle is one, we can easily find out the sine length given the cosine length, or the reverse, using the Pythagorean theorem.

It is important to remember that when you draw a radius line at any angle from the origin, these rules apply. The sine value $sin(\theta )$ will always be the distance on the y-axis between the point on the circle and the x-axis (labeled opposite on the image below). The cosine value $cos(\theta )$ is therefore the distance between the point on the circle and the y-axis (labeled adjacent on the image below). The triangle formed by these distances will always have a hypotenuse length equal to 1 (the radius of the circle). Therefore, using the Pythagorean theorem, we can see that:

$\sin ^{2}(\theta )+\cos ^{2}(\theta )=1$

Application of the Pythagorean Theorem to a trigonometric circle

Let's try an example with the cosine length equal to ${\tfrac {1}{2}}$ We now have enough information to able to convert the Pythagoras Theorem to get the value for the opposite sine length.

$c^{2}=a^{2}+b^{2}$

$1^{2}=a^{2}+{\tfrac {1}{2}}^{2}$

Since we don't have one of the legs of the theorem we must arrange the formula so that we can isolate the piece to the puzzle we don't know.

$c^{2}-b^{2}=a^{2}$

$1^{2}-{\tfrac {1}{2}}^{2}=a^{2}$

$1-{\tfrac {1}{2}}=a^{2}$

$0.75=a^{2}$

$a={\tfrac {\sqrt {3}}{2}}$

This method is quite simple and can also be used to solve the Cosine length, as long as we have one of the legs in the triangle.

Proposition for Basic Skills Project

We propose to put up information about the Pythagorean Theorem. We could put up some proofs, various applications of the theorem, how to use it, and other such things. This could certainly tie in to distance and lines, as well, as getting the distance between two points on a graph is essentially the same thing.

BenJeffery

---

Using information from the group members who responded (Christa, Marco, Ben):

Things we all can do well

10. Distance and Lines

12. Construction of Graphs

13a. Pythagorean Theorem

14. Areas and Volumes

15. Mathematical Writing

Things some of us can do well

3. Equations

4. Inequalities

5. Composition of Functions

8. Intersections of Functions

9. Reading Graphs of Functions

11. Operations on Graphs of Functions

13b. Trigonometry

Things none of us can do well

1. Basic Functions

2. Properties of Functions

6. Polynomial Long Division

7. Graphs of Functions