Course:MATH110/Archive/2010-2011/003/Groups/Group 16/Basic Skills Project

What is the "Graph of a Function"?

The graph of a function f is the collection of all possible pairs (x, f(x)) that can be found on the graph of f, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. This implies that, in order to find the intersection(s) of the graphs f and g, we need to be able to solve the equation f(x)=g(x), which is not always possible. We shall shown you one such case in the last section of this page. Right now we shall focus on more typical examples of graphs one encounters perhaps with a little bit more frequency.

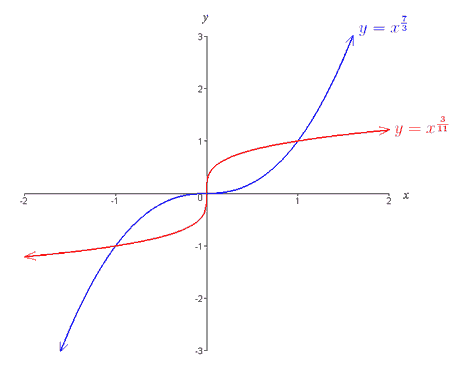
The plots below showcase some common power functions we have encountered in the course:

Find intersection of graphs

There are at least three types of intersections of graphs,

1. Intersection of parabolas

2. Intersection of linear lines

3. Intersection of a Parabola and a Line

4. Overview of the beautiful Descartes invention between the geometry and the algebra(reword)

5. Special case-Failed to parse (syntax error): {\displaystyle e^x = −x}

Intersection of power functions

Warm-Up Question

What is/are (a) possible scenario(s) for two parabolas appearing on the same coordinate plane?

a. 1 point of intersection only

b. 1 or 2 points of intersection

c. 2 points of intersection without exception

d. Depending on the magnitude of the plane in question, there can be infinite points of intersection

e. Others

f. Do I care?

The answer will come soon except perhaps for those that picked f. Right now, let’s look at how to find if two quadratic functions, f(x) and g(x), has any point of intersection.

$F(x)=1.5\times 2-9x+11.5$

$G(x)=-0.2\times 2-0.4x+2.8$

Finding intersection of power functions algebraically

If you understand the following concept, you will not even have to memorise the technique. The points of intersection are where both parabolas share the same (x, y) coordinates. So, at the points of intersection the (x, y) coordinates for f(x) equal the (x, y) coordinates for g(x). To put this into practice using f and g,

$1.5\times 2-9x+11.5=-0.2\times 2-0.4x+2.8$

From here find x if the equation is factoreble. If not, use the quadratic formula, and if there are points of intersection, $\vartriangle b^{2}-4ac$ will render one, or two, solutions. Alternatively, if $\vartriangle b^{2}-4ac$ render a negative root, that points to the fact that there are no points of interception of f and g.

How to predict the number of intersecting points between two or more power functions

If you want to find how many points of intersections there are between more than two functions, well, there's no special way. You might as well use the algebraic trick in the previous section to work out the point(s) of intersection, that will give you the number of intersections too. This is not limited to parabolas, but applicable to all power function types.

Tea Time

Get up and get something to drink/eat because you know you've been wanting to.

Answer to warmup question

If you have been such a star student and actually looked through this section for intersection points of power functions, you should have absolutely no trouble answering the warmup question. The answer is e. Or more precisely, two quadratic graphs (parabolas) can have one, two, or zero point of intersection. Since seeing is believing...

Visualising points of intersection for two quadratic equations

• One Single Point of Intersection

• Two Points of Intersection

• No Intersecting Points

Intersection of linear functions

Here we will cover how to find the point of intersection for two linear functions. That is, finding the (x, y) coordinate pair for the point where two lines cross.

We will be using these two linear functions as examples:

$F(x)=3x+18$

$G(x)=-10x+25$

Visualising how Two Lines Intersect on the Cartesian Plane

Where two lines cross is called their point of intersection. As you may or may not know, this intersection point has (x, y) coordinates. It is the same point for both linear functions, this means the (x, y) coordinates are the same for both linear functions of f(x) and g(x).

As we will be graphing the linear functions, we can call f(x) line 1 and g(x) line 2. We will be graphing the functions on a (x, y) coordinate plane therefore we can express the functions into slope-intercept form. That is, express them in equations of this form: $y=mx+b$:

$y=3x+18$

$y=-10x+25$

Finding Point of Intersection Algebraically

Since the (x, y) coordinates are the same for both lines at the point of intersection, we can first equate both functions in order to solve for ‘x’. By equating the two equations we have something like this:

Now that we have the x-coordinate for the point of intersection, we can move on to finding the y-coordinate. In order to find the y-coordinate, we can substitute the x-coordinate we found earlier into either of the equations and then solve for ‘y’.

We can use line 1 here:

$x=7/13$
$y=3x+18$
$y=3(7/13)+18$
$y=(21/13)+18$
$y=255/13$
$y=19.62$

Therefore, the y-coordinate is 255/13 or 19.62. If we want to make sure our calculations are correct, we can check by substituting ‘x’ into line 2 as it should produce the same answer.

$x=7/13$
$y=-10x+25$
$y=-10(7/13)+25$
$y=(-70/13)+25$
$y=255/13$
$y=19.62$

We see that the answer for the y-coordinate is the same, meaning this is the correct number. Therefore, the point of intersection for these two lines is (0.54, 19.62).

Intersection of a Parabola and a Line

The equation of the parabola is of the form

$y=ax^{2}+bx+c$

and the equation of the line is of the slope intercept form

$y=mx+b$

If $y=mx+b$ is substituted into $y=ax^{2}+bx+c$ , we end up with a quadratic equation given by:

$mx+B=ax^{2}+bx+c$

Solving the above will render the x coordinate(s) of the point(s) of intersection. To find the points of intersection, substitute the x coordinate values into one of the original equation of either the parabola or the line.

Predicting the Number of Intersecting Points between a Parabola and a Line

You can use the above procedure to find the intersection of any line with any parabola. Usually, the line and parabola will not always intersect at two points. Sometimes they will only intersect at one point, and quite often they will not intersect at all. These conditions will show up when you solve the quadratic equation after you set the two separate functions equal to each other. When solving that quadratic equation, if the discriminant (i.e. $b^{2}-4ac$ )equals a positive real number, you are going to get two solutions for x, which in other words predict that there will be two points of intersection between the two equations. If the discriminant equals zero, then you will have only one solution for x, which boils down to only one point of intersection. If the discriminant is negative, then there are no solutions for x, which means the two parabolas do not intersect.

Geometrically speaking, the number of solutions when you substitute $y=x$ into $y=ax^{2}+bx+c$ represents the number of times the line $y=x$intersects the parabola - any parabola with equation in the form of $y=ax^{2}+bx+c$. Now let us visualise what it all meant. Here we have a graph of the line y = x, along with three other parabolas representing the three possible cases of two, one, or zero intersections:

The line $y=x$ intersects with the Green parabola twice, with the Blue once, and never intersects with the Yellow one.

Implication of a Parabola and a Line Intersecting Exactly Once

The line is tangent to the parabola at their point of intersection. That also means that the equation of the line is the derivative function of the parabola. That is cool, isn't it?

Concept in Action

Now let us work on two questions that make use of the concepts we have learnt in this section. The questions are:

1. Does the parabola $y={\frac {x^{2}}{2}}-5x-10$ ever intersect the line $y=2$?

2. In how many points does the parabola $y=3x^{2}+4x-5$ intersect the line $y=-6$?

Overview of the Beautiful Descartes Invention between Geometry and Algebra

Why is Descartes a significant part of mathematics history?

René Descartes, often referred to as the father of analytical geometry, was the inventor of the Cartesian coordinate grid system. It is in Descartes system that the first coordinate value (x-coordinate) represents where the point is located along the horizontal axis (the x-axis). The second coordinate value (y-coordinate) represents where the point is in terms of the vertical axis (the y-axis). It is this system that allows us to illustrate the intersection of two lines, visually understand the relationship between coordinate points, equations and functions and much more. In other words, this system allows us to draw geometric shapes that are expressed as algebraic equations.

Special case $-e^{x}=-x$

Indeed, there are many more possible cases of graphs intersecting. Some of them are even impossible to find. Here we look at one example, $y=-x$ and $y=e^{x}$

It is clear to see, those two graphs intersect at one point. But we are never going to be able to find that point algebraically (yes graphically perhaps) - Why do you think that is?

We are not able to solve the equation $e^{x}=-x$ because it is unsolvable.

So, the idea is that it will be useful to keep in mind that there can well be intersections when functions are graphed. However, some of these actually can never be found algebraically.

---

References: