Homework #4

Question 1

Five persons named their pets after each other. From the following clues, can you decide which pet belongs to Suzan's mother?

- Tosh owns a cat,
- Bianca owns a frog that she loves,
- Jaela owns a parrot which keeps calling her "darling, darling",
- Jun owns a snake, don't mess with him,
- Suzan is the name of the frog,
- The cat is named Jun,
- The name by which they call the turtle is the name of the woman whose pet is Tosh,
- Finally, Suzan's mother's pet is Bianca.

The best way to tackle a problem such as this would be to go through each piece of information given and organise the data into a form much easier to go back to and make adjustments to. Below is a simple person to pet chart I drew up from the information given.

Tosh ---> Cat (Jun)

♀Bianca ---> Frog (Suzan)

♀Jaela ---> Parrot (No name)

♂Jun ---> Snake (No name)

♀Suzan ---> Turtle (No name)

With ♀ denoting female and ♂ denoting male, we can see in the table that the information has given us enough to start off with. We know Bianca is female from the statement "Bianca owns a frog that she loves" and we know that Jaela is also female from the statement "Jaela owns a parrot which keeps calling her 'darling, darling'". We also know that Jun is male from the statement "Jun owns a snake, don't mess with him", with him referring to the owner and not the pet, otherwise it would be saying don't mess with it.

We can also assume that Suzan's pet is the turtle since both are the only owner and pet that do not have a match and since the problem states that there are only five people then we can assume that there are also only five pets.

Next, we can assign the pet name Tosh to the only other female aside from Suzan, Jaela. We can do this because we know that Suzan's pet is the turtle and if the name by which they call the turtle is the name of the woman whose pet is Tosh then naming the turtle Tosh would mean that the turtle's name needs to be Suzan which is all very confusing and counter-intuitive.

♀Jaela ---> Parrot (Tosh)

This piece of information also allows us to name Suzan's pet because again the name of the turtle would be the name of the person whose pet is called Tosh. Thus we receive the next bit of information:

♀Suzan ---> Turtle (Jaela)

That only leaves the last part of the problem, which would be Jun's pet:

♂Jun ---> Snake (Bianca)

Though the logic may fit, this solution is wrong as Jun is supposedly male and Susan's mother cannot possibly be male unless the label "mother" is semantically misleading (i.e. nickname, etc.).

There are then two possible solutions after this error. The first is that the statement "Jun owns a snake, don't mess with him" has the pronoun 'him' refer to the snake, which can therefore make the solution of Jun owning the snake Bianca correct (although the male snake would be awkwardly named Bianca). This solution ends up with Jun being Suzan's mother and the pet Bianca being her pet.

The second solution could be that the turtle is not owned by Suzan. This would allow any other person to own the turtle, allowing the turtle to then be named Suzan and therefore allowing Suzan's pet to be Tosh and lastly having Jaela's pet to be Bianca (and thus having Jaela as Suzan's mother). This scenario assumes that Jun is male and assumes that since the definition of the problem never assigns a finite number of pets within the group or never limits the amount of pets that the group can have (or limits the doubling of names within those pets, etc.) that there is the possibility that each person can own more than one pet. The problem never states that the pets listed are the only pets that these individuals own and thus can be seen as a possible solution, and a more likely one then the previously aforementioned. In this case, it is not realistically possible to know who Suzan's mother is with the given information.

Question 2

Bohao, Stewart, Dylan, Tim and Chan are the five players of a basketball team. Two are left handed and three right handed, Two are over 2m tall and three are under 2m, Bohao and Dylan are of the same handedness, whereas Tim and Chan use different hands. Stewart and Chan are of the same height range, while Dylan and Tim are in different height ranges. If you know that the one playing centre is over 2m tall and is left handed, can you guess his name?

First, simplify the information:

Bohao, Stewart, Dylan, Tim and Chan

2 are left-handed, 3 are right-handed

Bohnao and Dylan = Same Hand

Tim and Chan = Different Hand

2 are over 2m, 3 are under 2m

Steward and Chan = Same Height

Tim and Dylan = Different Height

Need to find: player that is over 2 meters tall and left-handed

Now draw a diagram to help solve the first part of the problem (Left/Right Handed).

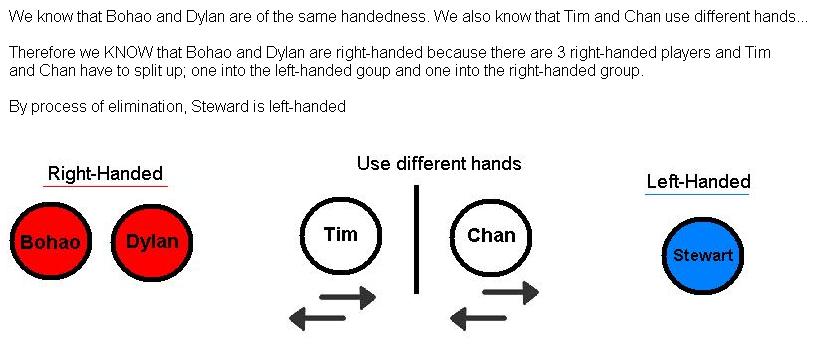
Now draw another diagram to help solve the final part of the problem (Above/Under 2 meters in height).

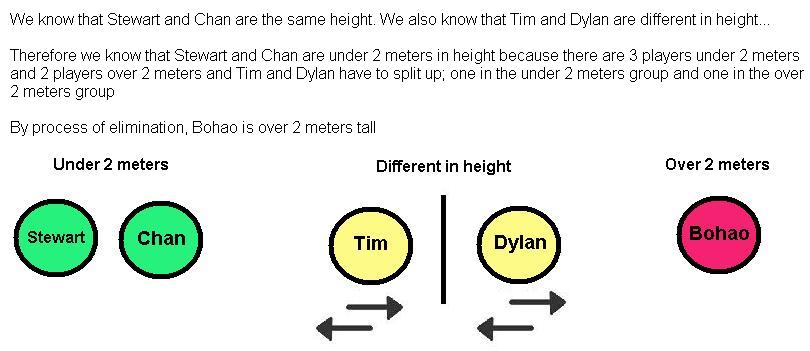
Now, using these two diagrams find a player that is over 2 meters tall and left-handed

By process of elimination we know that it can't be:

Bohao (right-handed)

Dylan (right-handed)

Stewart (Under 2 meters)

Chan (Under 2 meters)

Therefore it COULD only be TIM

Therefore the player that is over 2 meters tall and left-handed is TIM

Question 3

We are trying to determine which position everyone plays. I started by making a chart of all the players and all the positions so we could cross off possibilities as we went along. Then we started using the information we are given to figure out which position various people CANNOT play so as to start to figure out positions by process of elimination.

We are told the following (and our interpretation is written in parentheses, which we then marked on the chart accordingly)

1. Adam does not like the catcher, (so Adam cannot be the catcher)

2. Ed's sister is engaged to the second baseman, (so Ed cannot be the second baseman)

3. The centre fielder is taller than the right fielder,

4. Hassan and the third baseman live in the same building (so Hassan cannot be the third baseman)

5. Pascal and Charles each won $20 from the pitcher at a poker game (so neither Pascal nor Charles can be the pitcher)

6. Ed and the outfielders play cards during their free time (Ed cannot play outfield)

7. The pitcher's wife is the third baseman's sister,

8. All the battery and infield except Charles, Hassan and Adam are shorter than Sung (Charles, Hassan, and Adam play infield or battery and therefore do not play any of the outfield positions)

9. Pascal, Adam and the shortstop lost $100 each at the race track (neither Pascal nor Adam are the shortstop)

10. The second baseman beat Pascal, Hassan, Bobo and the catcher at billiards (none of Pascal, Hassan, or Bobo play either second base or catcher. And Adam is not going to be the second baseman because he doesn’t like the catcher and so would likely not play billiards with him.)

11. Sung is in the process of getting a divorce (So Sung cannot play second base because the second baseman is engaged.)

12. The catcher and the third baseman each have two legitimate children

13. Ed, Pascal Jason, the right fielder and the centre fielder are bachelors, the others are all married (none of Ed, Pascal, or Jason play right or center field. Also, none of them can play pitcher because the pitcher has a wife. Also, Sung will not play right or center field because he must be married in order to be getting a divorce and Ed, Pascal, and Jason cannot be catcher or third base because they would have to be married as per #12.)

14. The shortstop, the third baseman and Bobo all attended the fight (Bobo cannot play short stop or third base)

15. Mathieu is the shortest player of the team

At this point we see that Center and Right must be played by either Mathieu or Bobo because they are the only two possibilities left. #3 says the Center is taller than the Right and #15 says Mathieu is the shortest player so Mathieu must play Right and Bobo must play center. We then eliminate them from playing any other positions. We can then see that only Charles or Jason can play second base. Since the second baseman is engaged (#2) Jason has to be the second baseman (because #13 says the only bachelors by name are Ed, Pascal, and Jason ie. not Charles. So if Charles were to be a bachelor he would have to play right or center field.) So Jason plays second base and we eliminate him from all other positions. Left field is either Pascal or Sung. Since #6 says Ed plays cards with the outfielders and #5 mentions Pascal playing cards, let’s assume Pascal plays outfield. So Pascal plays left field and we eliminate him from all other positions. #4 says Hassan and the third baseman live in the same building and maybe they do because the pitcher’s wife is the third baseman’s sister (#7). Since Hassan can’t be the third baseman it might be reasonable to assume that he is the pitcher. #10 says that the catcher got beat at billiards. Since the catcher is either Sung or Charles but we’ve never heard anything else about Sung doing anything social with the others we’re going to assume that the catcher is Charles (who was playing poker in #5). Following the same logic the shortstop is mentioned to do quite a bit of gambling so I’m going to assume that that is Ed (who is mentioned to be a card player in #6 and he’s also a bachelor so it’s a little more likely for him to be out carousing than Sung.) That leaves just Adam and Sung and first and third base. Since we haven’t heard anything about first base but we know that the third baseman has legitimate children (#12) and we know Sung is married (because he’s getting divorced #11) it seems more reasonable to peg him as the third baseman, leaving Adam to play first base.

So the positions are:

Adam- First Base

Ed- Short Stop

Bobo- Center Field

Charles – Catcher

Hassan- Pitcher

Jason – Second Base

Mathieu – Right Field

Pascal – Left Field

Sung – Third Base

Question 4

Six players - Petra, Carla, Janet, Sandra, Li and Fernanda - are competing in a chess tournament over a period of five days. Each player plays each of the others once. Three matches are played simultaneously during each of the five days. The first day, Carla beats Petra after 36 moves. The second day, Carla was again victorious when Janet failed to complete 40 moves within the required time limit. The third day had the most exciting match of all when Janet declared that she would checkmate Li in 8 moves and succeeded in doing so. On the fourth day, Petra defeated Sandra. Who played against Fernanda on the fifth day?

First we have to look at each piece of information that is given to us. We know that there are 6 players, and that each player plays each other once in 5 days:

This means that there are 3 pairs playing against each other everyday

We are given enough information to determine a set of pairs for each day. Using this information, we can determine the other four players and who they play during the 5 days.

First we will group all the pairs that we know has played during the five days

Day 1: CP We have Janet, Sandra, Li and Fernanda leftover (J, S, L, and F)

Day 2: CJ (L, P, S, and F)

Day 3: JL (F, P, L, and S)

Day 4: PS (F, J, L, and C)

Day 5: F ?

Since we know the pairs that play each other, we can begin to group the leftover individuals together at random, while making sure that they only play each other ONCE, therefore we have to take into consideration the given pairs and the groupings we have assigned at random for the day BEFORE.

Day 1: "CP" "JS" "LF"

Day 2: "CJ" "LP" "SF" (We cannot group F with L again because they have played each other on the first day)

Day 3: "JL" "FP" "LS" (Make sure each player only plays each other once, F has already played S and L, therefore we can group her with P)

Day 4: "PS" "FJ" "LC"(Following the above format, for these four days, we have grouped each player with another player that they have not been grouped with before, we can see that Fernanda has played each player once, which leaves us with the last player, the player we are trying to determine. We will still group the rest of the individuals together to double check that they have indeed played each other once)

The grouping for the following day is as follows:

Day 5: "PS" "FJ" and "LC"

By following the information we have, we can follow the steps that are given to us and logically figure out who Fernanda played against on the last day. Not only does this give us the answer, but we have a listing of all the possible combinations, and who played against who for all five days.

Therefore, we can come to the conclusion that Fernanda played Janet on the last day.

Question 5

Answer: Homer sleeps late on Tuesday!

Sat - Salesman
Sun - Dog
Mon - Salesman and Construction
Tuesday - Homer sleeps late!
Wednesday - Salesman and Dog
Thursday - Construction and Dog
Friday - Salesman
Saturday - Construction
Sunday - Dog

Here, no pair has woken homer together for more than one day and they have not been quiet for three consecutive days.

Here is how I solved this problem.

1) I created a chart for Saturday throughout Sunday (similar to the one above) and filled in the provided information

Sat - Salesman
Sun - Dog
Mon - Salesman and Construction
Tuesday -
Wednesday - Salesman and Dog
Thursday -
Friday -
Saturday - Construction
Sunday - Dog

2) For the salesman to be noisy for at least once in three consecutive days, he must have had to be noisy on Friday

Sat - Salesman
Sun - Dog
Mon - Salesman and Construction
Tuesday -
Wednesday - Salesman and Dog
Thursday -
Friday - Salesman
Saturday - Construction
Sunday - Dog

3)Now, we need one day for Homer to rest undisturbed on Tuesday or Thursday. But for the dog and the construction to be noisy at least once in their three consecutive days, we can place the both of them on Thursday to satisfy the requirements. We can then determine that Homer had a happy sleep on Tuesday!

Sat - Salesman
Sun - Dog
Mon - Salesman and Construction
Tuesday - Homer sleeps late!
Wednesday - Salesman and Dog
Thursday - Construction and Dog
Friday - Salesman
Saturday - Construction
Sunday - Dog