Homework #3

Question 1

A bus traveled from the terminal to the airport at an average speed of 30 mi/hr and the trip took an hour and 20 min. The bus then traveled from the airport back to the terminal and again averaged 30 mi/hr. However, the return trip required 80 min. Explain.

60min = 1hour

60min + 20min = 80min

1hour + 20min = 80min

 Therefore to travel from the terminal to the airport at an average speed of 30mi/h in an hour and 20min is the same 
 as traveling from the airport back to the terminal at the average speed of 30mi/h in 80min because... 
  1hour and 20min = 80min

Question 2

A lady did not have her driver's license with her when she failed to stop at a stop sign and then went three blocks down a one-way street the wrong way. A policeman saw her, but he did not stop her. Explain.

The simple explanation to this question is that the lady is a pedestrian. Since she is not driving a car she does not need to have her license present with her, does not have to stop at STOP signs and may walk down a one way street going the wrong way. (On the sidewalk of course)

    Therefore the witness policeman did not stop her because she did NOT break the law.

Question 3

One of three boxes contains apples, another box contains oranges, and another box contains a mixture of apples and oranges. The boxes are labeled APPLES, ORANGES and APPLES AND ORANGES, but each label is incorrect. Can you select one fruit from only one box and determine the correct labels? Explain.

The problem can be solved by taking out the contents of Box #1. If an APPLE is pulled out of Box #1, you know that the contents of Box #1 is just APPLES. This is because the two options (labelled in blue) are either just APPLES or just ORANGES.

Given that Box #1 has only APPLES you know that Box #3 has APPLES & ORANGES. This is because the two options are just APPLES or APPLES & ORANGES and Box #1 already contains just APPLES.

By process of elimination Box #2 contains just oranges.

The same logic applies if an ORANGE is initially pulled out of Box #1. Then Box #2 would contain APPLES & ORANGES and Box #3 would contain just ORANGES.

      Therefore the solution can be solved by opening Box #1.

Question 4

I am the brother of the blind fiddler, but brothers I have none. How can this be?

   The key to this question is to avoid gender bias. The logical solution is that the boy is the brother 
                      of a blind fiddler, who is his sister, therefore he has no brothers.

Question 5

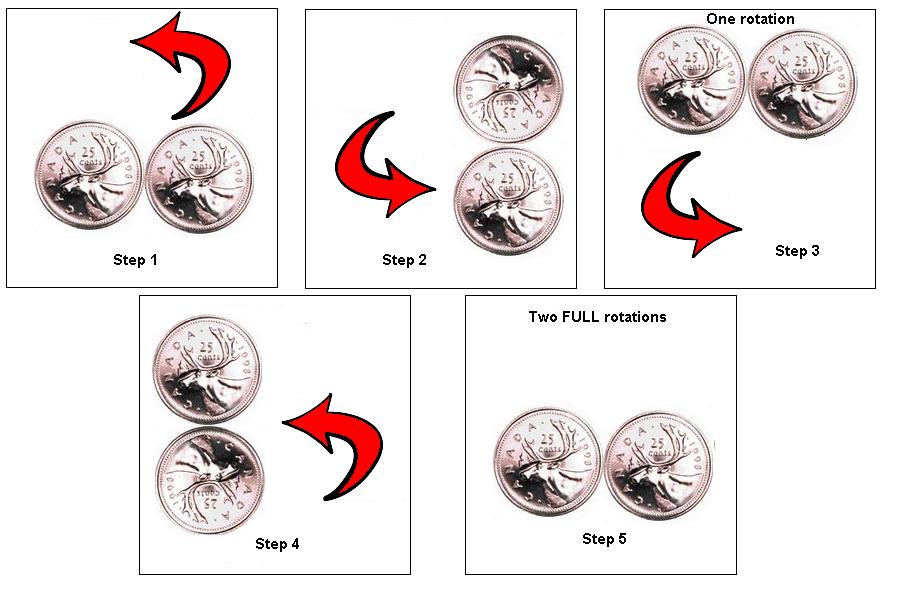
Two quarters rest next to each other on a table. One coin is held fixed while the second coin is rolled around the edge of the first coin with no slipping. When the moving coin returns to its original position, how many times has it revolved?

   Just follow the diagram and you will see that the coin is revolved twice when it returns to its original position.

Question 6

Three kinds of apples are all mixed up in a basket. How many apples must you draw (without looking) from the basket to be sure of getting at least two of one kind?

If we draw four apples from the basket, then we can assure ourselves that the fourth apple must be the same kind as one of the first three that we drew. Therefore, if we draw four apples, we would be sure of getting at least two apples of one kind.

Question 7

Suppose you have 40 blue socks and 40 brown socks in a drawer. How many socks must you take from the drawer (without looking) to be sure of getting (i) a pair of the same color, and (ii) a pair with different colors?

i) pair of the same colour

If we draw three socks without looking, we guarantee ourselves of drawing two socks that are of the same colour because there are only two kinds of colours that the socks can be.

ii) a pair with different colours?

If we draw 41 socks, than we can guarantee ourselves of drawing two socks that are different in colour. A person can have the fortunate (or unfortunate)event of drawing straight 40 socks of the same colour. But on his 41st draw, the sock must be of different color because there are no socks of the other color remaining.

Question 8

Reuben says, “Two days ago I was 20 years old. Later next year I will be 23 years old.” Explain how this is possible.

If Reuben's birthday was on Dec. 31st 2010 and he said this statement on Jan. 1st 2011, than one year later on Jan. 1st 2012, he would turn 23 years old in the same year.

Dec 30th 2010 - 20 years old
Dec 31st 2011 - turns 21
Jan 1st 2011 - Says that two days prior he was 20 years old and that he would turn 23 years old later next year.
Dec 31st 2011 (same year) - turns 22
Jan 1st 2012 (year after he makes his statement) - will be turning 23 in this year

Question 9

A rope ladder hanging over the side of a boat has rungs one foot apart. Ten rungs are showing. If the tide rises five feet, how many rungs will be showing?

If the tide rises by five feet, the tide will also raise the boat by five feet also. Therefore, ten rungs would still be showing.

Question 10

Suppose one-half of all people are chocolate eaters and one-half of all people are women. (i) Does it follow that one-fourth of all people are women chocolate eaters? (ii) Does it follow that one-half of all men are chocolate eaters? Explain.

i and ii)

It does not follow that both one-fourth of all people are women chocolate eaters or that one-half of all men are chocolate eaters. The information that we are provided does not say anything about which people are chocolate eaters. It only tells us that half of all people are chocolate eaters and that half of all peopole are women.. In an alternate reality, given that half of all people are chocolate eaters and half of all people are women, it could be that all women in this reality eat chocolate, which negates both numbers i and ii.

Question 11

A woman, her older brother, her son, and her daughter are chess players. The worst player’s twin, who is one of the four players, and the best player are of opposite sex. The worst player and the best player have the same age. If this is possible, who is the worst player?

First, we have to figure out who the worst and best player are, we know that the worst and best players are of opposite sex and have the same age, therefore the twins are the worst and best player. But because we have limited knowledge, ie we do not know the ages of the four players, or what gender the worst and best player is, we can technically conclude that all four can be the worst player. The woman and her older brother can be twins OR the son and the daughter could be twins. Therefore this situation is not possible.

Question 12

A Manhattan fellow had a girlfriend in the Bronx and a girlfriend in Brooklyn. He decided which girlfriend to visit by arriving randomly at the train station and taking the first of the Bronx or Brooklyn trains that arrived. The trains to Brooklyn and the Bronx each arrived regularly every 10 minutes. Not long after he began his scheme the man's Bronx girlfriend left him because he rarely visited. Give a (logical) explanation.

Because each of the trains arrive 10 min apart, we can come up with a train schedule:

Bronx train arrives at 10:10, 10:20, 10:30 etc. Brooklyn train arrives at 10:09, 10:29, 10:20 etc. Because the man arrives at any given time/random time, we can see that unless he arrives exactly between the time the Brooklyn train leaves the and Bronx train arrives, we can see that the Brooklyn train will always arrive first, and that the only chance he will have to take the Bronx train is during that one minute interval. The probability or chances he has of arriving during exactly during that one minute interval is very slim. Therefore we can come to the conclusion that because the Brooklyn train always arrives before the Bronx train, the man usually ends up getting on the Brooklyn train because it is the first to arrive; this makes his visits to his Bronx girlfriend very infrequent and rare.

Question 13

If a clock takes 5 seconds to strike 5:00 (with 5 equally spaced chimes), how long does it take to strike 10:00 (with 10 equally spaced chimes)?

For each 5 seconds the clock chimes 5 times with equal lengths of space in between. Each second there is one space, so in total there are 4 spaces in between each chime. In order to calculate how many seconds it takes for 5 chimes and 4 stops, we can divide 4 by 5. 5 chimes / 4 spaces = 1.25seconds So when there are 10 equally spaced chimes, we can conclude from the above example that in between each chime there is one stop. 10 chimes has 9 stops in between (because it stops at the 10th chime we do not count the 10th stop). We can then find out how long it takes. ( 9 stops * 5 seconds ) / 4 stops = 11.25 seconds to strike 10:00

Question 14

One day in the maternity ward, the name tags for four girl babies became mixed up. (i) In how many different ways could two of the babies be tagged correctly and two of the babies be tagged incorrectly? (ii) In how many different ways could three of the babies be tagged correctly and one baby be tagged incorrectly?

i). First we have to start by having two names be labeled correctly, for example A and B are labeled correctly while C and D are mixed up. In order to have A and B be labeled on the correct baby, C and D can only be mixed up twice, there are only two alternatives while keeping A and B on the right baby. Since we can arrive at the solution that for each combination of 2 there are 2 answers. We have to test it out for pair of babies. AB = ABCD, ABDC We can go through ABCD and figure out that in that four letter sequence there are six possible pairing combinations AB, AC, AD, BC, BD, CD and that each of these pairs can have two of the other single letters mixed up therefore, 6 * 2 = 12, the answer gives us that there can be 12 possible combinations.

ii). Logically if we think about the question asked, how many ways could three babies be tagged correctly and one baby be tagged incorrectly, the question does not make sense. Because there are 4 babies, if 3 babies are tagged correctly then the fourth one MUST be tagged correctly because there leaves no other alternative/baby to be tagged. Therefore there are no ways that three of the four babies could be tagged correctly since having three tagged correctly means that all four are tagged correctly.

Question 15

Alex says to you, “I'll bet you any amount of money that if I shuffle this deck of cards, there will always be as many red cards in the first half of the deck as there are black cards in the second half of the deck.” Should you accept his bet?

Each deck of cards has 52 cards, where they are either red or black: 26 red cards and 26 black cards. No matter how Alex splits the deck, there should always be an equal amount of red cards to black cards. For example, if Alex splits the deck in two (each deck containing 26 cards) we see that there are 12 black cards and 14 red cards. Because there are an equal number of black and red cards, the second deck should have the same number or cards with the reverse color combination. Therefore no matter how many different ways Alex splits the deck, the colored cards in one deck will always equal the opposite colored cards in the other desk because they have to equal to 26 (the number of cards in the deck and the number of red/black cards).

-Alex splits the deck, first deck has 10 BLACK cards and 16 RED cards = second deck has 10 RED cards and 16 BLACK cards

-Alex splits the deck, first deck has 3 BLACK cards and 23 RED cards = second deck has 3 RED cards and 23 BLACK cards etc etc.

We can come to the conclusion that because the cards are equal in value, that no matter how Alex splits the deck, the red cards will equal the black cards in a split deck.

Question 16

Suppose that each daughter in your family has the same number of brothers as she has sisters, and each son in your family has twice as many sisters as he has brothers. How many sons and daughters are in the family?

Trying to figure out how many S (sons) and D (daughters) so I tried to represent the information in an expression.

Daughters-1 = Sons (because when you take away the daughter who is counting her siblings the # of daughters will = # of sons) and Sons = (Daughters/2)-1 (because when you take away the son who is counting there will be twice as many daughters as sons)

So there always needs to be 2 daughters for every son, which will grow pretty rapidly and, I think, exclude the possibility that a daughter could have equal # brothers and sisters (because there will just be too many daughters.) So I think it might only work if there is only one son. Then each daughter has 1 brother and 1 sister, and each son has twice as many sisters as brothers ( ie 0 brothers).

Question 17

The zero point on a bathroom scale is set incorrectly, but otherwise the scale is accurate. It shows 60 kg when Dan stands on the scale, 50 kg when Sarah stands on the scale, but 105 kg when Dan and Sarah both stand on the scale. Does the scale read too high or too low? Explain.

If the scale read too low then we know that D’s real weight would be >60 kg and S’s real weight would be >50kg and so we would expect their combined weight to be >than their weights combined (or 110 kg). Since it is less than this, the scale must read too high. Which makes sense because if D’s real weight is <60 and S’s real weight is <50 then we would expect the outcome to be <their combined weight (110kg).

Question 18

Alice takes one-third of the pennies from a large jar. Then Bret takes one-third of the remaining pennies from the jar. Finally, Carla takes one-third of the remaining pennies from the jar, leaving 40 pennies in the jar. How many pennies were in the jar at the start?

I thought of this by thinking of what was always left in the jar. There is always 2/3 of the previous jar amount left (because someone removes 1/3). So then I just worked backwards. I asked “40 is 2/3 of what number? That must be how much was in the jar before.” Turns out 40 is 2/3 of60. I continued in this manner until I had calculated back the appropriate removals and determined that the number of pennies in the jar to start with was 135.

Question 19

One morning each member of Angela's family drank an eight-ounce cup of coffee and milk, with the (nonzero) amounts of coffee and milk varying from cup to cup. Angela drank a quarter of the total amount of milk and a sixth of the total amount of coffee. What is the least number of people in the family?

Angela’s cup can be expressed as: ¼ Total Milk + 1/6 Total Coffee = 8 oz We can also say that: Total Milk + Total Coffee/8 = # of family members (because they each had an 8 oz cup)

If the smallest amount of people in a family would be two (because that’s the smallest number bigger than 1) then we could substitute that in to see if it works:

8 x 2 = 16 (total coffee and total milk) Which is a totally reasonable conclusion. So the least number of people in the family is 2 because that is the least number (other than 1, which wouldn't really count as a family) that this works with.

Question 20

Of two clocks next to each other, one runs 5 min per hour fast and the other runs 5 min per hour slow. At midnight the clocks show the same time. At what time are they are one hour apart?

For each hour of time that passes Clock A gains 1hr + 5 minutes and Clock B gains 1 hr -5 mins. This means that there is always an increasing difference between them and the difference is always increasing by 10 minutes. So if we want to know when they will be an hour apart it’s when they have had their 10 minute difference compounded 6 times, so 6 hours after they started, or 6 o’clock (by real time. Clock A would show 6:30 and Clock B would show 5:30)

Question 21

Sven placed exactly in the middle among all runners in a race. Dan was slower than Sven, in 10th place, and Lars was in 16th place. How many runners were in the race?

First we have to recognise Sven's place, which is exactly in the middle. This definition implies that the number of people in the race is an odd number since in even numbers it is impossible to be exactly in the middle. This gives the following definition of:

Total = 2(Sven) - 1

We also know that Sven came in before Dan, who is 10th. Thus giving the definition:

Sven < 10

Lastly we know that Lars came in 16th, thus adding another aspect to the equality given for the total number of runners:

Total = 2(Sven) - 1 > 16

The only number satisfying both inequalities of Sven being less than 10 and the total being greater than 16 is Sven being ninth place. All numbers under nine make the total runner inequality untrue (i.e. 2(7)-1 = 15), thus making the total number of runners 17.

Question 22

During a vacation, it rained on 13 days, but when it rained in the morning, the afternoon was sunny, and every rainy afternoon was preceded by a sunny morning. There were 11 sunny mornings and 12 sunny afternoons. How long was the vacation?

Let x be the number of rainy afternoons, which can also be seen as the number of sunny mornings, as given by the statement "every rainy afternoon was preceded by a sunny morning".

Let y be the number of rainy mornings, which can also be seen as the number of sunny afternoons, as given by the statement "when it rained in the morning, the afternoon was sunny".

Let z be the number of days where it didn't rain at all.

From these definitions we can come up with equations to represent these pieces of information.

For one we can say that $x+7=11$ since every rainy afternoon was preceded by a sunny morning but not every sunny morning led to a rainy afternoon (i.e. some sunny mornings led to a sunny afternoon).

Next we can say that $y+z=13$ since every rainy morning led to a sunny afternoon, but every sunny afternoon does not entail a rainy morning before it.

Lastly we can say that $x+y=13$ since the number of rainy mornings and rainy afternoons obviously equals the number of days it rained.

Then we can simply solve the system of equations.

$y+x=13$
$x=13-y$
$x+z=11$
$13-y+z=11$ and $y+z=12$
$12-11=y+z-(13-y+z)$
$1=y+z-13+y-z$
$1=2y-13$
$y=7$

$y+x=13$ --> $7+x=13$ --> $x=6$

$y+z=12$ --> $7+z=12$ --> $z=5$

Thus $x+y+z=7+6+5=18$ , with 18 being the length of the entire vacation.

Question 23

Suppose you overhear the following conversation: Paul: How old are your three children? Paula: The product of their ages is 36 and the sum of their ages is the same as today's date. Paul: That is not enough information. Paula: The oldest child also has red hair. If you were Paul could you determine the ages of Paula's children? Explain.

First, the strongest clue in the conversation with Paula is that the three ages of the children have a product of 36. This limits the numbers to being combined factors of 36.

To start off, you can easily list down all of the 3-set factors of 36 which are:

{ ( 36, 1, 1)
(18, 2, 1)
(12, 3, 1)
(9, 4, 1)
(9, 2, 2)
(6, 6, 1)
(6, 3, 2)
(4, 3, 3) }

The next clue is that the sum of these ages would equal today's date, thus the sum of their ages cannot exceed 31.

Adding all the ages of the 3-set factors would yield the following:

36 + 1 + 1 = 38
18 + 2 + 1 = 21
12 + 3 + 1 = 16
9 + 4 + 1 = 14
9 + 2 + 2 = 13
6 + 6 + 1 = 13
6 + 3 + 2 = 11
4 + 3 + 3 = 10

Next, since Paul says that giving that clue is not enough information, we can conclude that the ages are either (9, 2, 2) or (6, 6, 1) since if it was any other 3-set combination, the sum is unique leaving no room for uncertainty.

Lastly, Paula says that the oldest child has red hair, thus implying that there is only one oldest child. Since if the oldest children indeed shared their age as in the case of (6, 6, 1) then the statement would read something like "my oldest children have red hair". Thus leaving only the set of (9, 2, 2) left.

Question 24

Two candles of equal length were lit at the same time. One candle took 6 hr to burn out and the other candle took 3 hr to burn out. After how much time was one candle exactly twice as long as the other candle?

Both candles were at equal length when they were lit, given by L. With one burning out after 6 hours and the other after 3 hours. From this we can see a progression of the first candle having the equation:

$L=((6-t)/6)$ with t being the number of hours elapsed since the candle was lit

The second candle's equation is as follows:

$L=((3-t)/3)$ with t again being the number of hours after the candle was lit

Following the values given by substituting t with increasing multiples of 1 we achieve the criteria in the question after 2 hours:

$((6-1)/6)=5/6$ <----> $((3-1)/6)=2/3$

$((6-2)/6)=4/6$ <----> $((3-2)/6)=1/3$

$4/6=2/3$ $2/3=2(1/3)$ with 1/3 being the length of the second candle.

Thus giving the answer as after 2 hours.

Question 25

Two candles of length L and L + 1 were lit at 6:00 and 4:30, respectively. At 8:30 they had the same length. The longer candle died at 10:30 and the shorter candle died at 10:00. Find L.

Let t = 0 be the time at which the longer candle is lit (i.e. 4:30).

Since when L is at half its length, namely $(1/2)L$ , it equals 4 or 4 hours after 0, then we can put up the equation:

$(1/2)L=4$
$L=8$

L then equals 8.