Course:MATH110/Archive/2010-2011/003/Groups/Group 11/Basic Skills: Trigonometric Functions

Math 110/003 - Group 11
Members:	Abdul-Sherif Abdul-Rahaman
	Shannon Lee
	Amir Mohamad Nazri
	Matt Vetter

Basic Skills Project: Trigonometric Functions

This page will focus on trigonometric function. Group 11 hopes that through providing examples, and step-by-step solution guides we can eliminate the struggles many of us face in regards to solving problems involving trigonometry. Hopefully after reviewing this page you will be able to relate trigonometric functions to the study of everyday occurrences, some of which include: waves, daily temperature averages through the seasons, alternating current, electronic signals, as well as other cyclic phenomena. In the "Just-in-Time" text book, chapter 7, titled "Cyclic Phenomena: The Six Basic Trigonometric Functions," can provide further assistance when reviewing trig functions.

A trigonometric function, also known as a circular function, is a function that relates the lengths of the sides of a right triangle with the angles of the triangle. The basic trig functions are sine, cosine, tangent, cotangent, secant and cosecant.

• (x)=sin x and f(x)=cos x are functions defined for any real number x.

The other basic trigonometric functions we also have to remember are

1)tangent: tan x = sin x/ cos x

2)cotangent: cot x = cos x/sin x

3)secant: 1/cos x

4)cosecant: 1/sin x

For our course however, we will not be using the trigonometric functions cot, csc or sec. It is helpful to remember that these are just functions derived from sin and cos.

Right-angled Triangle Definition

If a value of x falls between 0 and π/2, so 0<x<π/2 then the definition of sin(x) and cos(x) is called the right-angled triangle definition. By this definition, sin(x)=opposite/ hypotenuse and cos(x)=adjacent/hypotenuse. A helpful pneumonic for remembering how to solve the sides of a right triangle is SOH CAH TOA!

Caption: Right Triangle.

Function	Abbreviation	Description	Trigonometric Identities using Radians
Sine	sin	${\frac {\textrm {opposite}}{\textrm {hypotenuse}}}$	$\sin \theta =\cos \left({\frac {\pi }{2}}-\theta \right)={\frac {1}{\csc \theta }}$
Cosine	cos	${\frac {\textrm {adjacent}}{\textrm {hypotenuse}}}$	$\cos \theta =\sin \left({\frac {\pi }{2}}-\theta \right)={\frac {1}{\sec \theta }}\,$
Tangent	tan	${\frac {\textrm {opposite}}{\textrm {adjacent}}}$	$\tan \theta ={\frac {\sin \theta }{\cos \theta }}=\cot \left({\frac {\pi }{2}}-\theta \right)={\frac {1}{\cot \theta }}$
Cotangent	cot	${\frac {\textrm {adjacent}}{\textrm {opposite}}}$	$\cot \theta ={\frac {\cos \theta }{\sin \theta }}=\tan \left({\frac {\pi }{2}}-\theta \right)={\frac {1}{\tan \theta }}$
Secant	sec	${\frac {\textrm {hypotenuse}}{\textrm {adjacent}}}$	$\sec \theta =\csc \left({\frac {\pi }{2}}-\theta \right)={\frac {1}{\cos \theta }}$
Cosecant	csc	${\frac {\textrm {hypotenuse}}{\textrm {opposite}}}$	$\csc \theta =\sec \left({\frac {\pi }{2}}-\theta \right)={\frac {1}{\sin \theta }}$

To Begin learning about trigonometric functions, lets review the unit circle:

Caption: The Unit Circle.

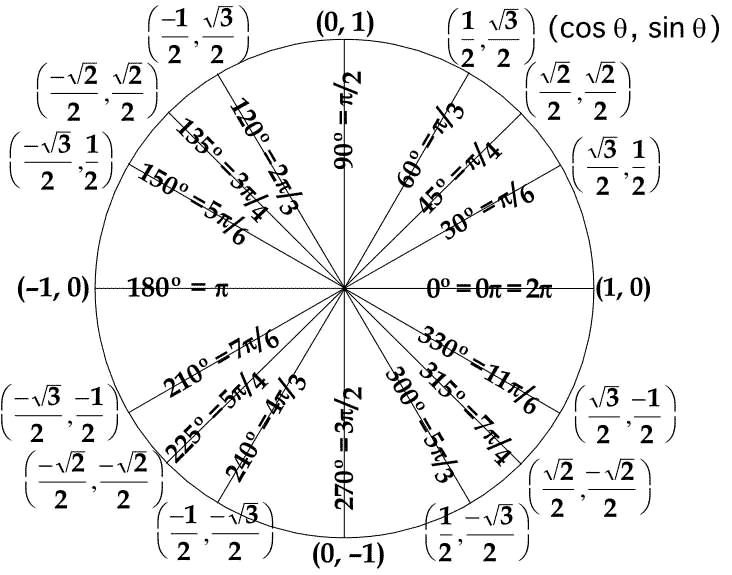
What do sine and cosine represent?(optional)
The x coordinate on the unit circle is cos(x), and the y coordinate is sin(x) (x,y) = (cos(x), sin(x)).

Because cos(x) and sin(x) is a point on the unit circle, its coordinate must satisfy the equation of the circle: x^2+y^2 = 1

Therefore, Sin^2(x)+cos^2(x) = 1

• The unit circle has a radius = 1
• The circumference of the unit circle = 2π radians

each complete rotation of the unit circle will add 2π or 360°, for instance 2 complete revolutions of the unit circle = 4π or 720°,

On the Unit Circle, x and x + 2π correspond to the same point, this fact means that the graphs of y=sin(x) and y=cos(x) repeat over and over again, and gives us sin(x) = sin(x + 2kπ), where k is any whole number and represents the number of revolutions. From this we can say that sin(x) has a period of 2π. This can also be said about cos(x).

Converting Degrees to Radians
Angle *(2π/360°) for example: Convert 27° into radians: 27°*(2π/360°)= (3/40)*2π = 3π/20

Converting Radians to Degrees
Radian * n(π), where π is equal to 180° for example: Convert 3π into degrees 3π = 3(180°) = 540°

Different approach to the conversions

Of course there are multiple ways doing conversions between radians and degrees. Another way of doing it can be demonstrated below: Example 1: Convert 3π into degrees 3π x (180/π) = 540° Example 2: Convert 27° into radians: 27° x (π/180) = 3π / 20 As calculated, no matter what your approach is towards the conversion calculation, the end result is the same. The purpose of this example is just to remind you that there are more than one option towards solving a problem. If one way does not work, try another. This is good exercise to sharpen up your mathematical skills

The following is a helpful video for understanding the Unit Circle. The man who makes this video is very a great teacher and is very clear and concise. It can help you to understand and remember the points on the unit circle. This will help when it comes to solving trigonometric problems.

Special Triangles

It is helpful to keep a couple of tips in mind when working with trigonometric functions. Since a lot of conversions are made in between radians and degrees remembering these two triangles may save time calculating:

Using the special triangles
As shown above, these three triangles can be use in order to calculate the exact values for sine(x), cosine(x) and Tan(x) for x equals to 1π/6, 1π/4 and 1π/3

Applying the special triangles
By memorizing the triangle you can directly compute the values of the following: Sin π/6 = (Opposite / Hypotenuse) = 1/2 Cos π/6 = (Adjacent / Hypotenuse) = ${\sqrt {3}}/2$ Tan π/6 = (Opposite / Adjacent) = $1/{\sqrt {3}}$

Applying the special triangles
This can also be applied to π/4 and π/3 $\sin(\pi /4)={\sqrt {1/2}}$ Cos π/4 = $1/{\sqrt {2}}$ Tan π/4 = 1 Sin π/3 = ${\sqrt {3}}/2$ Cos π/3 = 1/2 Tan π/3 = ${\sqrt {3}}$ In order to check the accuracy of these values, you can also check with the graph of each respective sine, cosine and tangent function.

The CAST / ASTC Rule

Caption: The Cast Rule.

The Cast Rule is an easy way to remember which trigonometric functions are positive and negative in any of the four quadrants of the Cartesian Plain.

- Going from the first quadrant, you will notice the A in this section. This means that ALL trigonometric functions are positive in the first quadrant

- Moving into the second quadrant, you will see the S which represents the fact that all Sine functions are positive in this section, while the Tangent and Cosine functions are negative

- The third quadrant, where the T is located, is the section where only Tangent functions are positive and Sine and Cosine functions are negative

- Finally in the fourth quadrant, where the C is located, only Cosine is positive, while Sine and Tangent functions are negative.

- Another good way to remember the order is simply by associating each letter with something common or easy to remember with. Going from quadrant I to quadrant IV, each letter can be associated with All Soup Turns Cold,or All Science Teachers Cheat where each bold letter in the sentence is a representative of "All positive", "Sine Positive", "Tan positive" and "Cosine positive". This is an easy way to identify which trigonometric function is negative or positive depending on which quadrant they are in.

Solving Trig Functions

Examples:

1.)Evaluate $\cos(3{\boldsymbol {\pi }}/2)$and $\sin(3{\boldsymbol {\pi }}/2)$:

To determine the sine and cosine values of angles using the unit circle is quite simple. If you refer back to the picture of the unit circle above, you can see that 3π/2 is three quarters of the way around the unit circle and located at the point (0,-1). If you remember that (x,y) is equivalent to (cos(x), sin(x)), then we can determine that:

$\cos(3{\boldsymbol {\pi }}/2)=0$ and $\sin(3{\boldsymbol {\pi }}/2)=-1$

2.)Evaluate $\cos(9{\boldsymbol {\pi }}/2)$:

To solve this problem, we first need to determine that $9{\boldsymbol {\pi }}/2$ is equivalent to $4{\boldsymbol {\pi }}+{\boldsymbol {\pi }}/2$. A complete revolution of the unit circle is = 2π; therefore, 4π is just equal to two complete revolutions of the unit circle, which does not change the value of your answer. So $\cos 4{\boldsymbol {\pi }}+{\boldsymbol {\pi }}/2$ is equal to two complete rotations and another quarter rotation, or 90°. If we refer to the unit circle above, we can see that π/2 is equal to (0,1). Because cosine is equal to the x value, we can determine that:

$\cos(9{\boldsymbol {\pi }}/2)=0$

For some extra practice in evaluating the angles of sin and cos, 
refer to the exercises in chapter 7.2 of your Just-in-Time text!

Finding Special Angles

examples:

1.) Evaluate $\sin({\boldsymbol {\pi }}/4)$

Solution: Failed to parse (syntax error): {\displaystyle \boldsymbol{\pi}/4 = 45°}

Caption: Sin and Cos of 45°.

The coordinates of the point in the question are (cos(x) and sin(x), x=\boldsymbol{\pi}/4. The equation of the circle is $\sin ^{2}(x)+\cos ^{2}(x)=1$,

therefore, $\sin ^{2}({\boldsymbol {\pi }}/4)+\cos ^{2}({\boldsymbol {\pi }}/4)=1$

so if we let s represent the unknown side values of the triangle (cos(x),sin(x))then,

$\sin ^{2}({\boldsymbol {\pi }}/4)+\cos ^{2}({\boldsymbol {\pi }}/4)=s^{2}+s^{2}=2s^{2}=1$

$2s^{2}=1,s^{2}=1/2,s=+/-{\sqrt {1/2}}$

$s={\sqrt {1/2}}$

so $\sin {\boldsymbol {\pi }}/4={\sqrt {1/2}}$

This video gives some great examples of how to evaluate the angle of \sin and \cos. It is also good for learning how to use the unit circle when solving these problems. Solving Trigonometric Functions:

Graphing Trigonometric Functions

Sine graphs

If sin(x) is plotted on a set of "x" and "y" axis, the graph of sin(x) would be drawn as shown below:

Caption: The Sine Curve

The demonstration above is to show how the values from the unit circle can be plotted onto a set of "x" and "y" axis. The graph is not limited, it depends on a given scope. In other words, as long as the range of the sin function is not given, sin(x) graph will repeat as a wave until infinite. The sin(x) graph below shows for x values from 0 to 4π.In order to calculate the points where slope = 0, we must make equate the derivate of sin(x) = 0.

Caption: Graph of sin(x)

Cosine graphs

Cosine have the exact same characteristics to that of a sine graph. The only difference between the two is that cosine function shifts to the right by a factor of 90° or π/2 in radians:

y = cos(x)

Caption: Graph of cos(x)

As mentioned previously, cosine functions have the exact same behavior as the sine graph, and the only difference between them is that cosine functions shifts to the right by a factor of 90° or π/2 in radians. Mathematically speaking, if we were to expressed cos(x) in terms of sin(x), it would be written as; cos(x) = (sin(x+π/2)). The comparison between a sine and a cosine function is demonstrated as below;

Caption: Cosine Curve

Tangent Graphs

Caption: Graph of tan(x)

How does the Tan (x) above drawn?

Any values for tan x is basically the computed values of (sin x/cos x), mathematically speaking tan x = (sin x / cos x). As shown above, tan x has asymptotes at x =Failed to parse (syntax error): {\displaystyle π/2} , 3π/2...etc. Referring back to the sine and cosine graphs, if we were to take the values for sine π/2 and cosine π/2, sine π/2 would equal to 1, and cosine π/2 would equal to 0. Since 1/0 can't be define, tan x would not be able to be compute of x = π/2. The end result of this is an asymptote as Tan x would always be getting closer and closer to, but never reach. The following video will provide you with a more clearer visual explanation of this concept:

Transformations

General trigonometric function

The following table is a standard form of writing general trigonometric functions. This example is use to write the standard sine function: You may be wondering about the terms that are given above in the general form, the diagram below shows what each terms correspond to in a trigonometric graph: In other words, amplitude is simply the maximum displacement of a graph from the principal axis. For instance in a case where y = sin(x), the amplitude of the sine graph is equivalent to "1". Whereas if it is y = 2sin(x), the amplitude is equal to "2". On the other hand, "period" is the distance between any two repeating coordinate on the graph, and is calculated by T=2π/B. As for Cosine, Tangent and other trigonometric functions, their standard form would look as shown below: Caption: Translating Graphs If the visual explanation is not able to assist you in the problem, watch the following video. It is a great tutorial on how to graph Trigonometric functions. This video gives an in-depth tutorial on the transformations of Trigonometric functions. Pay attention closely to the "period", "amplitude" and of course both the horizontal and vertical translations. Try your best to come up with a function and graph it by referring to the method shown in this video tutorial:

Sources

• Owen, John "Mathematics For The International Student"

• "Special triangles" http://www.mrhiggins.net/classroom/2010/10/

• "Pre-Calculus-graphing the tangent" http://www.youtube.com/watch?v=O_tmzW_J6V4

Basic Skills Project-Group Contribution

http://wiki.ubc.ca/Course:MATH110/003/Groups/Group_11/Basic_Skills