Course:LFS252

LFS 252 Land, Food, and Community: Quantitative Data Analysis
Course Info
Instructor 001:	Carol McAusland
Email:	Carol.McAusland@ubc.ca
Office:	MCML 337
Office Hours:	Th 12:30-1:30pm
Schedule:	Tu/Th 8:00-9:20am
Classroom:	Hennings 200

LFS 252 (3) Applied Data Analysis for Land and Food Systems: Introduction to tools needed for data analysis of the economic, ecological, health, and scientific components of land and food systems.

Prerequisites: LFS 250 and at least one of MATH 100, 102, 104, 180, or 184.

Textbook: Elementary Statistics: A Step-by-Step Approach. 2nd Canadian Edition. Allen G. Bluman and John G. Mayer. 2011. McGraw-Hill Ryerson.

Instructor: Prof. Carol McAusland

Teaching Assistants:

• Gabrielle Menard (OH: 5-7pm Thursdays MCML 139) Gabrielle.Menard@ubc.ca
• Jennie Phasuk (OH: 12-2pm Mondays MCML 139) SuvapornPhasuk@gmail.com
• Sean Holawaychuk (OH: 2-4pm Wednesdays MCML 139) Sean.Holowaychuk@gmail.com
• Katie Neufeld

Course Description

This course is designed to give students the ability to analyze data and critique statistical techniques used in land and food systems. Particular attention is paid to sampling procedures. The course integrates data analysis with data collection activities in LFS 250, 350, and 450. Students will also learn statistical techniques and software, which will allow them to conduct more rigorous analysis of data for upper level courses throughout the Faculty of Land and Food Systems.

This course consists of three hours of lecture per week. In addition, there are voluntary tutorial sessions in which students can receive help with homework assignments.

Learning Objectives

• Organize and interpret scientific and social data related to agriculture, food, and the environment.
• Assess and interpret statistical results presented in relevant scientific literature.
• Analyze and critique survey design.
• Select and apply appropriate statistical measures and techniques.
• Identify appropriate measures and techniques, including basic statistics that can be used to evaluate aspects of agri-food systems.
• Critique statistical measures and derived conclusions.

Method of Delivery

There are two lectures per week; lecture slides will be available before the lecture.

Software: Students will learn R for data analysis. Demonstrations of the software form part of the formal lectures and tutorials. The assignments and Lab Exam require the use of R.

Course Outline

• Chapter 1: The Nature of Probability and Statistics
• Chapter 2: Frequency Distributions and Graphs
• Chapter 3: Data Description
• Chapter 4: Probability and Counting Rules
• Chapter 5: Discrete Probability Distributions
• Chapter 6: The Normal Distribution
• Chapter 7: Confidence Intervals and Sample Size
• Chapter 8: Hypothesis Testing
• Chapter 9: Testing the Difference Between Two Means, Two Variances, and Two Proportions
• Chapter 10: Correlation and Regression
• Chapter 11: Other Chi-Square Tests
• Chapter 12: Analysis of Variance
• Chapter 13: Nonparametric Statistics (if time permits)
• Chapter 14: Sampling and Simulation (if time permits)

Tutorials

Attendance at tutorials is highly recommended. Tutorials will be held in MCML 192 at the following times:

• Mon 10:00 - 11:00 am (Gabrielle Menard)
• Mon 11:00-12:00 pm (Jennie Phasuk)
• Tues 9:30-10:30 am (Sean Holowaychuk)
• Wed 1:00-2:00 pm (Jennie Phasuk)
• Thurs 10:00-11:00 am (Gabrielle Menard)
• Thurs 3:00-4:00 pm (Sean Holowaychuk)

At the tutorials, teaching assistants will introduce students to the statistical software R and the supported interface, RStudio. The teaching assistants will provide guidance on commands that can be used to execute the homework assignments. This will also answer questions regarding previous assignments and concepts from lecture.

Assessment

Students will be assessed based on their performance on weekly quizzes, occasional computer assignments, a midterm exam, a lab exam, and a final exam. The quizzes will be taken online via McGraw-Hill's Connect Website. The midterm will take place on February 26. The dates of the lab and final exams will be announced midway through the semester. The computer assignments will not be graded. As the assignments form the basis for the lab exam and thus 30% of the final grade, students are strongly urged to complete the assignments in a timely fashion.

Activity	Value of Overall Grade
Quizzes (1% each)	10%
Assignments	0%
Midterm Exam	30%
Lab Exam	30%
Final Exam	30%

Quizzes (all due by 11:59PM)

1 Jan 16

2 Jan 23

3 Jan 30

4 Feb 6

5 Feb 13

6 Mar 6

7 Mar 13

8 Mar 20

9 Mar 27

10 Apr 10

Previous LFS 252

Statistics

Descriptive Statistics: are used to graphically or numerically describe the observed sample allowing for summarizations about the represented 'population'. These representations include mean, median, mode, standard deviation, frequency, probability, percentages .......

Inferential Statistics: draw inferences about the sample population through pattern analysis.

Scales of Measurement

Nominal data: Labels or names are used to identify characteristics of elements that are difficult to rank. Labels can also be numeric codes that are arbitrarily assigned. Nominal data is a form of categorical (or qualitative) data and is measured on a discrete scale.

Examples: place of birth, blood type, gender, marital status

Ordinal data: Data can be ranked. Order is meaningful, but the degree of difference between data is not expressed. Ordinal data is a form of categorical (or qualitative) data and is measured on a discrete scale.

Examples: Apple grades, military ranks

Interval data: Data has all properties of ordinal data, but also expresses degree of difference between data. The zero value is arbitrary. Interval data is quantitative.

Examples: years, temperature

Ratio data: Data has all properties of interval data, but the zero value is meaningful. The ratio between two values can be expressed. Ratio data is quantitative.

Examples: velocity, weight

Central Tendency

Mean: the central tendency of a set of numbers, taken by dividing the sum of all the numbers by the amount of numbers in the set.

Median: when a collection of numbers in arranged in increasing order, the middle number of the collection is known as the median, if there is an even amount of numbers in the data set then the median is found by taking the mean of the two middle numbers. The median is used primarily for skewed distributions. It is also useful for comparing data sets, like the mean.

Mode: the value that occurs the most frequently in a data set. Not all data sets will have a mode.

Distribution:In probability theory and statistics, a probability distribution identifies either the probability of each value of a random variable (when the variable is discrete), or the probability of the value falling within a particular interval (when the variable is continuous)

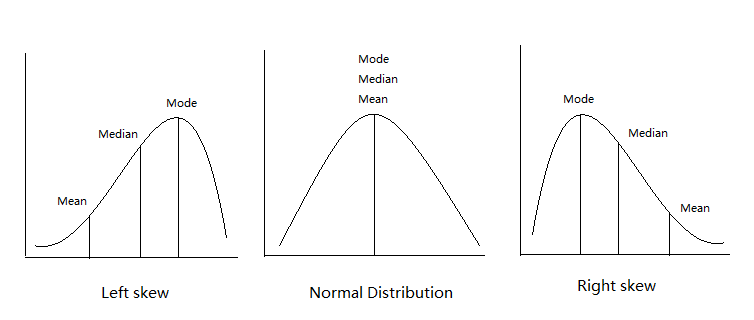
Normal Distribution: The mean, median and mode are all equal. The data is distributed as a normal bell curve, which is symmetric about the mean/median/mode.

Standard Deviation: A measure of variability to show how much "dispersion" exists from the average. A low standard deviation indicates that the data points tend to be very close to the mean, whereas high standard deviation indicates that the data points are spread out over a large range of values.

How to find SD from a sample set with "n" values

• 1. Subtract each value from the mean
• 2. Square these differences then add them up
• 3. Divide this sum by n-1
• 4. Take the square root

Skewed Distribution: The data is not distributed symmetrically. More than one half of the data lies to one side of the mode.

Left Skew: This is when the bulk of the data lies on the right-hand side of a curve; the median is to the right of the mean. The tail of the graph is to the left. This indicates a negative skew and that the bulk of the values (possibly including the median, lie to the right of the mean.

Right Skew: This is when the bulk of the data lies on the left-hand side of a curve; the median is to the left of the mean. The tail of the graph is to the right. This indicates a positive skew indicates and that the bulk of the values lie to the left of the mean.

Correlation

Correlation is a single number between (-1.00, +1.00) that describes the degree of relationship between two observed variables. Graphically, a positive slope on a plot point graph indicates a positive relationship between the two variables. Meaning, as one factor increases so does the other. Naturally a negative slope indicates a negative relationship between the two variables. Meaning, as one factor increases the other decreases.

• Positive example: Exercise and life expectancy.

 -The more a person exercises on average the longer they are expected to live. 

• Negative example: exercise and body fat.

 -An increase in exercise frequency leads to a decrease in percent body fat.

Sampling

Sample Space: Sample space is the body from which a sample may be taken. For example. There is a bowl containing an apple and an orange which means there is an equal chance of randomly selecting an apple or an orange. Also known as sampling frame.

Sampling without replacement: There is a bowl filled with 5 apples and 5 oranges. One apple is removed and eaten. This has now changed the sample space. You are also leaving a probability of selecting the remaining apples and oranges as follows: P(O) 5/9 and P(A) 4/9

Sampling methods:

• Simple random sampling: Every member within the population has an equal chance of being sampled. A random number generator or a table of random numbers is used to select the samples.
• Systematic sampling: A random sampling process where every "n"th member of the sampling frame is selected and sampled periodically.
• Stratified sampling: The population is divided into subgroups or strata, then simple random sampling is conducted in each of the stratum.
• Cluster sampling: Elements of population are divided to groups or cluster (i.e. geographical), all the clusters are given equal chances of being selected, by simple random sampling.

Probability

Complement: The complement of an event A, is the set of all outcomes that are not A.

• The probability of an event and its complement occurring will always sum to 1.
• Probability of complement occurring is 1-(Probability of A occurring)

Mutually exclusive events: When two events cannot occur at the same time and are in no way connected. For example a person can either go to party A or party B but not both.

• Using the addition rule P (A or B)= P(A)+ P(B)- P(A and B). As you cannot attend both parties at the same time P(A and B)=0. Therefore the P(A or B)= P(A)+P(B)

Union of Events: Probability that A will occur, B will occur or both will occur (can be one or the other or both).

• Union=or
• Must use the addition rule to account of double counting: P (A or B)= P(A)+ P(B) - P(A or B).

Intersection of Events: Probability that both events will occur.

• Intersection="and"
• For independent events only, the probability of intersection is equal to P(A)P(B) (the product of both probabilities).

"Independent Variable"- example is fat: (person can't change the fat content but the fat can change the persons view on the product, therefore it is independent)

Independent Events: An event is independent if the outcome of the first event will not affect that of the second event. For example rolling a die.

Disjoint events: The probability of both events occurring at the same time is zero.

• P (A and B)=0

Note: Disjoint events are not independent. This means that the outcome of the first event will effect the outcome of the second event. For example say you have a bag of 5 green marbles and 6 blue marbles. The chance of you picking a blue marble is 6/11 and the chance of you picking green is 5/11. You pick a blue marble and do not replace it. Now the probabilities have changed to 5/10 for a green marble and 5/10 for a blue marble. The first event has affected the second event.

Correlation and Regression -Deals with the Relationships between variables A and B

 -ex. weight and height

-intake of food and gaining weight as a person/animal -In a perfect relationship r will equal 1, and then there can be positive 1+ and negative relationships 1- -If the correlation co-efficient equals 0, there is no relationship between the dependent and independent variables

Pearson Product Moment Coefficient

• is symbolized by r which provides the direction of the correlation
• to calculate r= observed coverance/max possible co-variance

--> r= observed coverance/square root of [(variance A) x (variance B)]