Course:KIN570/TOPICS/Significance Testing

Research Methods in Kinesiology
KIN 570
Section:	001
Instructor:	Nicola Hodges
	Jenny
Email:	<add your email here, if you want to>
Office:
Office Hours:
Class Schedule:
Classroom:
Important Course Pages
	Syllabus
	Lecture Notes
	Assignments
	Course Discussion

Comparing means and assessing relationships in Kinesiology Research

Standard deviation vs. standard error

Standard deviation (s, σ): dispersion of the data, deviation from mean, ȳ; the typical distance between each observation, y_i, and mean.

Standard error (SE): uncertainty of the mean due to sampling error; variability associated with ȳ itself.

• In other words, if you were to resample the data, how different would the mean be?

Here’s another way to think about standard deviation vs standard error: as your sample size approaches infinity, the sample mean approaches the population mean, the sample standard deviation approaches the population standard deviation, and the standard error approaches 0.

As n → ∞,

ȳ → μ

s → σ

SE → 0

When we do statistical significance testing, if we reject the null hypothesis, we’re saying that we are sufficiently (depending on $\alpha$) confident that our results are not due to sampling error.

Independent t-test

We use an independent t-test to compare the means of 2 independent sample groups.

Assumptions

1. Observations are made from normally distributed populations
2. Observations represent random samples from populations
3. Numerator and denominator of test statistic are independent and estimates of the same population variance

To conduct a significance test, we calculate the t-statistic, t_s, which is a ratio of the variability between groups to the variability within groups (or, the ratio of the variable of interest to the standard error of that variable)

$t_{s}={\dfrac {{\overline {y_{1}}}-{\overline {y_{2}}}}{SE_{({\overline {y_{1}}}-{\overline {y_{2}}})}}}={\dfrac {{\overline {y_{1}}}-{\overline {y_{2}}}}{\sqrt {{\frac {s_{1}^{2}}{n_{1}}}+{\frac {s_{2}^{2}}{n_{2}}}}}}$

The t-statistic answers the question, how many SE’s separate ȳ₁ from ȳ₂ ?

The larger the magnitude of t_s, the more likely it will produce a p-value less than $\alpha$. As we can see from the formula above, increasing the difference between the group means, decreasing the variances, or increasing the sample sizes will increase t_s and, consequently, increase the chance of finding statistical significance.

If:	ts:	Chance that p < $\alpha$:
(ȳ1 - ȳ2) increases	increases	increases
s1, s2 increase	decreases	decreases
n1, n2 increase	increases	increases

Paired t-test

We use a paired, or dependent, t-test to compare paired samples from 2 different groups - for example, strength before and after participation in an exercise program. In this case, we are more interested in the difference, d_i, between one sample and its pair than the actual magnitude of the samples.

Assumptions:

1. Differences between samples (d_i‘s) are regarded as random samples from a large population
2. Population distribution of d_i’s must be normal or approximately normal with a large n

The t-statistic calculation is slightly different from the independent t-test:

• Since we’re looking at the differences between the samples, we define our variable of interest as

${\overline {d}}={\overline {y_{1}}}-{\overline {y_{2}}}$ = ${\dfrac {\sum {d_{i}}}{n}}$

where ȳ₁ and ȳ₂ are the sample means of group 1 and group 2, and $n\$ is the number of samples in each group.

• Thus, calculation of the t-statistic becomes

$t_{s}={\dfrac {\overline {d}}{SE_{\overline {d}}}}={\dfrac {\overline {d}}{\sqrt {\frac {s_{d}^{2}}{n}}}}$

Again, t_s represents a ratio of the variability between groups to the variability within groups, which in this case is the variability of ${\overline {d}}$ itself.

Analysis of Variance (ANOVA)

We use ANOVA to compare the means of two or more groups (although usually three or more since we can use a t-test for 2 groups). We shouldn't use repeated t-tests for more than two groups because it increases the chance of type I error.

The null and alternative hypotheses are:

H₀: μ₁ = μ₂ = μ₃ = …

H_a: at least 1 mean is not equal to the others

Instead of calculating a t-statistic to find the associated p-value, we calculate the F statistic, F_s. Like the t-statistic, it is a ratio of variability between groups to variability within groups:

$F_{s}={\dfrac {MS_{bet}}{MS_{within}}}$

where:

$MS_{bet}={\dfrac {SS_{bet}}{df_{bet}}}$

which is a measure of how far, on average, each group mean is from the grand mean (the average of all observations pooled together); and where:

$MS_{within}={\dfrac {SS_{within}}{df_{within}}}$

which is a measure of how far, on average, an observation is from its respective group mean. The actual magnitudes of the group means have no influence on MS_within.

Post-Hoc Testing

If we reject the null hypothesis, all we know is that at least one of the means is not equal to the others, but we don’t know how many or which ones. To determine that information, we use a post-hoc test. The more conservative a test is, the more difficult it is to find statistical significance. Some examples, from most conservative to most liberal, are Scheffe, Tukey, Newman-Keuls, and Duncan.

Correlation

Correlation analysis involves looking at the relationship between 2 variables: when X changes, how does Y change? In this case, we’re assuming that if a relationship does exist between the variables, it’s linear.

Regression (best-fit) line

The best fit line is defined as the line that minimizes the following parameter, the sum of squares of the residuals:

$SS_{resid}=\sum (y_{i}-{\hat {y_{i}}})$

where $y_{i}\$ is the actual sample observation, and ${\hat {y_{i}}}$ is the value predicted by the regression line corresponding to $x_{i}\$

We can use 2 metrics to assess how well the best fit line fits the data:

• Correlation coefficient, $r\$: how accurately we can predict y_i given x_i
  • range: -1 to 1, where -1 and 1 indicate that the data fits the regression line perfectly (-/+ represent a -/+ slope of the regression line, respectively), and 0 indicates a very poor fit to the regression line
• Coefficient of determination, $r^{2}\$: the portion of the total variation that is accounted for by the regression line (this value is literally the correlation coefficient squared)
  • range: 0 to 1, where 1 indicates that all data points fall on the regression line, and 0 indicates a very poor fit between the data and regression line

Significance of Correlation

When we calculate the p-value associated with r, what we’re actually assessing is the chance of finding a regression line with a non-zero slope, assuming that in actuality, there is no relationship between the variables X and Y. Thus, we set our hypotheses as:

H₀: b₁ = 0

H_a: b₁ ≠ 0

where b₁ is the slope of the regression line

The t-statistic is calculated as:

$t_{s}={\dfrac {b_{1}}{SE_{b_{1}}}}=r{\sqrt {\dfrac {n-2}{1-r^{2}}}}$

If there were no relationship between X and Y, the slope of the regression line would be 0: a change in X produces no (consistent or predictable) change in Y. What we calculate with the t-statistic is the chance of getting a slope the size of b₁, assuming that the actual slope of the regression line is 0. So when we reject the null hypothesis, we are concluding that we are confident enough that a relationship exists – not that the actual slope is b₁.

For example: you're looking at the relationship between two variables, X and Y, in a population. Let's say you collect data on a sample group (size $n\$), and your data looks like this:

Figure 1: imaginary data from sample group with regression line shown. X and Y are paired samples. b₁ ≈ 1.

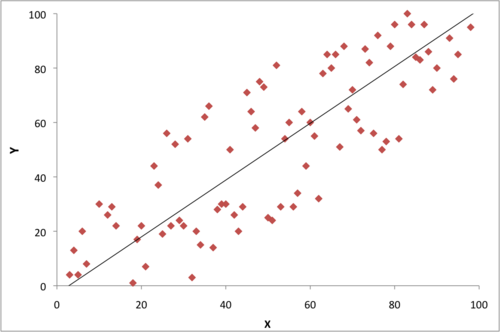
Qualitatively, we can see that there seems to be a definite trend: as X increases, Y increases (a positive correlation). This correlation is also reflected in the fact that the slope of the regression line is not 0 (i.e. the line is not horizontal). In fact, b₁ is ≈ 1. What we want to know is whether this relationship between X and Y actually exists in the larger population ($N\$ >> $n\$), or if we just collected a misleading sample. So we conduct a t-test in which our null hypothesis is b₁ = 0. The question that we're trying to answer is this: assuming the actual population distribution of X and Y looks like this (figure 2):

Figure 2: imaginary data from whole population. X and Y are paired samples. Regression line would be approximately horizontal with b₁ ≈ 0.

what are the chances that our sampled data would look like it does (figure 1)? In more mathematical terms: assuming there is actually no relationship between X and Y (b₁ = 0) in the larger population, what are the chances that our sample of the population produces a regression line with a slope as large as b₁ = 1? If our p-value turns out to be .01, that means finding a slope of b₁ = 1 would only happen by chance once in 100 times. In that case, we would generally conclude that p is significant and that our sampled data is not drawn from the population in figure 2. Note that we are not saying that we are 99% (1-p) sure that the actual regression line slope in the larger population is ≈ 1. We are simply saying that there is probably some degree of positive correlation between X and Y in the larger population.

References:

Additional resources

1. Thomas et al. (2005). Research Methods in Physical Activity. Windsor, ON: Human Kinetics. <Ch. 8 and 9>
2. Samuels & Witmer (2003). Statistics for the Life Sciences. Upper Saddle River, NJ: Pearson Education, Inc.
3. Berg & Latin (2004). Essentials of Research Methods in Health, Physical Education, Exercise Science, and Recreation. Baltimore, MD: Lippincott Williams & Wilkins. <Ch. 10 and 11>