Course:CPSC532:StaRAI2020:LearningBayesianNetworks

Learning Bayesian Networks: Ordering-Based Search and Entropy-Based Pruning

This page covers the complementary incremental contributions toward BN-learning from Ordering-Based Search: A Simple and Effective Algorithm for Learning Bayesian Networks (2005) and Entropy-based pruning for learning Bayesian networks using BIC (2018)

Authors: Andrew Evans

Abstract

Bayesian Networks are very effective tools for modelling probabilistic processes. When given a set of real-world data with many associated variables, it can be quite useful to model the data-generating process using a Bayesian network; this can provide insight into the nature of the data, and can be used to make predictions about the true data generating process. For these reasons, learning Bayesian Networks from data is of significant interest. Given the high computational complexity of BN-learning, significant effort has been put into creating algorithms and tools which are able to improve the performance of this computation.

Related Pages

This page covers methods of generating Bayesian Networks from data, optimized for a given criterion.

Content

BN-learning

Both ordering-based search and entropy-based pruning are incremental contributions in the learning of Bayesian Networks, also called BN-learning. This is the task of generating a Bayesian network structure which is best able to model a given data set of random variables. The definition of ‘best’ is unfortunately not universal for this problem; although the goal is to maximize the predictive capability, many different scores have been used to this end. In practice, common scores used include information-theoretic scoring functions such as the Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC), as well as Bayesian scoring functions such as the Bayesian Dirichlet Score with likelihood equivalence (BDe). These scores all measure slightly different things, though can be loosely thought of as measuring how closely a model matches a given data set. They are ideal under different sets of asymptotic assumptions about the data generating process and how it is modeled; the choice of scoring function is therefore not trivial in practice.

Ordering-Based Search: A Simple and Effective Algorithm for Learning Bayesian Networks

Motivation

BN-learning is an NP-Hard problem, and most standard solutions thus rely on heuristic approaches. The baseline approach to this problem is a greedy hill-climbing search, augmented by using a tabu-list to avoid reverting recent changes to the network structure during the search (DAG-search). This approach has proven quite effective, and is difficult to beat in practice. Most existing methods generally perform searches over the space of possible structures, and tend to be very complex and difficult to implement. This paper introduces a new approach; performing a search over possible orderings of network variables, instead of searching over potential graph structures. This proves advantageous, as finding the best network consistent with a given ordering is a much easier problem, and performing the search over orderings leads to more global modifications with each step, better avoiding local optima.

Ordering-Based Search

Ordering-based search divides the initial problem into multiple stages. First, a pre-computation stage is performed, which is common across many BN-learning algorithms. In this stage, potential families (comprised of a node and its parent nodes) can be determined or discounted based on heuristics. The number of possible parent nodes is also restricted by an upper bound $k$, a common restriction among BN-structure learning algorithms to prevent over-fitting of data, and to ensure this stage can be performed in polynomial time.

Next, a search is performed over possible orderings of the set of random variables $\chi =\{\mathrm {X} _{1},...,\mathrm {X} _{n}\}$ using greedy local hill-climbing and a tabu list. That is, each step in the search is performed by swapping two adjacent variables in the ordering, comparing the score after the swap, and taking the ordering with the highest score. This is done for all potential successor orderings for the current ordering, with a tabu list used to keep track of recent swaps, which can be checked to prevent undoing recent operations and helps avoid local minima while searching. In addition to those advantages previously mentioned, one advantage of this method is that the search space is heavily reduced, with $2^{{\text{O}}(n\log n)}$possible orderings instead of $2^{\Omega (n^{2})}$possible network structures. Although additional steps must be taken to compute the ideal network for a given ordering, this task is much less computationally intensive than searching over network structures globally, taking time ${\text{O}}(n^{k})$ per node.

For each ordering encountered in the search, two things must be obtained; the optimal network consistent with that ordering, and the score of that network. First, a network is considered consistent with an ordering if, for all variables $\mathrm {X} _{i}$, the parent nodes of $\mathrm {X} _{i}$ precede it in the ordering. Given that a scoring function is decomposable (that the score is the sum of scores for each family), caching can be used to improve performance. For each step in the ordering search, the possible set of parent nodes for a given variable $\mathrm {X} _{i}$ remain unchanged except for those variables which were swapped. Because the score is decomposable, only the optimal families for those variables which were swapped need to be recomputed, and the same holds for their scores.

Although this improves the performance of the search greatly, the computational cost of generating all necessary scores for all potential families of the initial ordering is very high. First, a list of potential families are computed for each node, each of which is ordered by score. Next, pruning is used is to eliminate families from contention based on their scores. For a given node $X_{i}$ and potential families $U$ and $U'$ where $U\subset U'$ , the family $U'$ can be eliminated from contention if $score(X_{i},U')\leq score(X_{i},U)$, which further improves performance during the search. Unfortunately, the above pruning rule relies on calculating the score of all potential families first, and can therefore only be used to discount them after the lists have been generated; they cannot be applied to the pre-computation stage to reduce the computational cost of generating the initial ordering.

Results

DBe score versus computation time in seconds for ordering-search (thick line) and DAG-search (thin line) methods, on the Diabetes network [Andreassen et al., 1991] dataset.

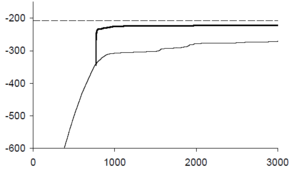
The ordering-based approach to BN-learning was used with the above criteria, with an additional heuristic pruning procedure used in the pre-computation stage which pre-selected small sets of candidate families for each variable, discounting others. This pruning condition is not necessarily sound, as it restricts the search space to arrangements in which no families are far from local optima, which may not hold for the true optimum. When comparing ordering search to DAG-search, using BDe as a score, several facts become apparent. Comparisons were made using many different datasets, some synthetic and some real. DAG-search was able to determine potential network structures earlier, as the pre-computation stage of ordering-based search is computational expensive. However, ordering-based search converged much faster, and always gave an equal or higher-scoring network in each tested example. This clearly demonstrates the improvements of using a more global search space, and that ordering-based search is an effective tool for BN-learning.

Entropy-based pruning for learning Bayesian networks using BIC

Motivation

Pruning potential families from consideration is an important stage in ordering-based search and other approaches to BN-learning. As previously mentioned, this can be done by exploiting the decomposable nature of most scoring functions. approximately correct heuristics are often used to impose additional constraints and reduce the complexity of the problem, but these may unintentionally remove high quality structures, and even the globally optimal structure, from contention. Some previous works have investigated using more precise pruning rules based on the scoring function being used, such as when using BDe. This work investigates additional, provably correct constraints on potential families when using BIC as the scoring function for categorical data. This can be used to improve performance of existing BN-learning algorithms when using BIC, including ordering-based search, without relying on approximate heuristics.

Pruning Rules

Several pruning rules are presented and discussed, including a number of existing rules (lemmas 1-3) and several new ones, including their proofs. In the following expressions, LL is log likelihood, H is (the sample estimate of) entropy, and Pen is the complexity penalization of BIC, defined as

${\text{Pen}}(\mathrm {X} _{i}|\Pi _{i})={\text{BIC}}(\mathrm {X} _{i}|\Pi _{i})-{\text{LL}}(\mathrm {X} _{i}|\Pi _{i})=-{\frac {\log _{b}N}{2}}(|\Omega _{\mathrm {X} _{i}}|-1)|\Omega _{\Pi _{i}}|$

for a given data set $D$, where $\Pi _{i}$ is a potential parent set of nodes for $\mathrm {X} _{i}$, $\Omega _{\mathrm {X} _{i}}$is the state space of $\mathrm {X} _{i}$ (such that $|\mathrm {X} _{i}|$ is the number of possible categories for $\mathrm {X} _{i}$), $|\Omega _{\Pi _{i}}|=\prod _{\mathrm {X} \in \Pi _{i}}|\Omega _{X}|$, and $N$ is the number of entries in the data set $D=\{D_{1},...,D_{N}\}$, where each entry $D_{i}$ is a complete assignment of all categorical random variables in $\chi =\{\mathrm {X} _{1},...,\mathrm {X} _{n}\}$.

Lemma 1.

As previously mentioned, for a given node $X_{i}$ and potential families $U$ and $U'$ where $U\subset U'$ , the family $U'$ can be eliminated from contention if $score(X_{i},U')\leq score(X_{i},U)$. Writing this in terms of parent sets $\Pi$ and $\Pi '$in place of families $U$ and $U'$, and using BIC as the scoring function, the list of candidate parent sets is

$L_{i}=\{\langle \Pi _{i},{\text{BIC}}(X_{i}|\Pi _{i})\rangle ~|~\forall ~\Pi _{i}'\subset \Pi _{i}:{\text{BIC}}(\mathrm {X} _{i}|\Pi _{i})>{\text{BIC}}(\mathrm {X} _{i}|\Pi _{i}')\}.$

Although this is useful for search optimization, it requires calculating the score of all candidate sets first, and so cannot be used to improve the performance of generating the initial conditions of the search.

Lemma 2.

Let $\Pi \subset \Pi '$ be candidate parent sets for node $\mathrm {X} \in \chi$. Then ${\text{LL}}(\mathrm {X} |\Pi )\leq {\text{LL}}(\mathrm {X} |\Pi '),~~{\text{H}}(\mathrm {X} |\Pi )\geq {\text{H}}(\mathrm {X} |\Pi ')$, and ${\text{Pen}}(\mathrm {X} |\Pi )>{\text{Pen}}(\mathrm {X} |\Pi ')$.

Lemma 3.

Let $\mathrm {X} \in \chi$ be a node with two candidate parent sets $\Pi \subset \Pi '$, such that ${\text{BIC}}(\mathrm {X} |\Pi )\geq {\text{Pen}}(\mathrm {X} |\Pi ')$. Then $\Pi '$ and all its supersets can be discarded when building the list of candidate parent sets for $\mathrm {X}$.

Lemma 4.

Let $\Pi =\Pi '\cup \{Y\}$ for $Y\not \in \Pi '$, where $\Pi$ and $\Pi '$ are candidate parent sets of $\mathrm {X} \in \chi$. Then ${\text{LL}}(\mathrm {X} |\Pi )-{\text{LL}}(\mathrm {X} |\Pi ')\leq N\cdot {\text{min}}({\text{H}}(\mathrm {X} |\Pi ');{\text{H}}(Y|\Pi '))$

Theorem 1.

Let $\Pi$ be a parent set for $\mathrm {X} \in \chi$. Let $Y\in \chi \backslash \Pi '$ such that $N\cdot {\text{min}}({\text{H}}(\mathrm {X} |\Pi ');{\text{H}}(Y|\Pi '))\leq (1-|\Omega _{Y}|){\text{Pen}}(\mathrm {X} |\Pi ')$. Then the parent set $\Pi =\Pi '\cup \{Y\}$ and all its supersets can be safely ignored when building the list of candidate parent sets for $\mathrm {X}$.

Theorem 2.

Let $\Pi ',\Pi ^{*}$ be parent sets for $\mathrm {X} \in \chi$, where $\Pi '\subset \Pi ^{*}$. Let $Y\in \chi \backslash \Pi ^{*}$ such that $N\cdot {\text{min}}({\text{H}}(\mathrm {X} |\Pi ');{\text{H}}(Y|\Pi '))\leq (1-|\Omega _{Y}|){\text{Pen}}(\mathrm {X} |\Pi ^{*})$. Then the parent set $\Pi =\Pi ^{*}\cup \{Y\}$ and all its supersets can be safely ignored when building the list of candidate parent sets for $\mathrm {X}$.

Theorem 3.

There is an optimal structure such that variable $\mathrm {X} \in \chi$ has at most

${\begin{matrix}{\text{max}}\\{Y\in \chi \backslash \{\mathrm {X} \}}\end{matrix}}\left\lceil 1+\log _{2}{\Biggl (}{\frac {{\text{min}}\{{\text{H}}(\mathrm {X} );{\text{H}}(Y)\}}{(|\Omega _{\mathrm {X} }|-1)(|\Omega _{Y}|-1)}}{\Biggr )}+\log _{2}N-\log _{2}\log _{b}N\right\rceil ^{+}$

parents, where $\lceil \cdot \rceil ^{+}$denotes the smallest natural number greater than or equal to its argument.

Results

Several of the above pruning rules were tested in varying combinations on both synthetic and real-world datasets, to determine the effectiveness of each one on its own, and in tandem with other rules. The runtime and number of parent sets pruned were tracked for each combination of rules (with no significant difference between the runtime of each algorithm), and for each dataset. Ultimately, it was found a computationally efficient set of rules pruned between 20% and 50% more candidate parent sets than previous methods. The effectiveness of these pruning rules varied significantly between datasets, however; in some cases, the vast majority of candidate parent sets could be pruned from the data, while in others (such as for the 'vote' UCI dataset), they had almost no effect. Although the authors of this paper report only on the effect this has in the preprocessing stage of BN-learning algorithms, it is clear that ordering-based searches would benefit significantly from their use when using BIC as a scoring function. In many cases, this could eliminate the need for the unsound heuristic pruning conditions used in the original implementation of ordering-based search.

Annotated Bibliography

Put your annotated bibliography here. Add links where appropriate.

To Add

Put links and content here to be added. This does not need to be organized, and will not be graded as part of the page. If you find something that might be useful for a page, feel free to put it here.