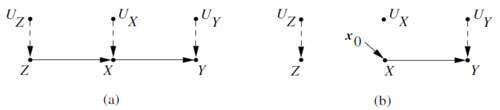Course:CPSC532:StaRAI2020:Causality

Title

Causality and Missing Data

Authors: Andrew Evans

Abstract

Causal analysis is a technique for answering complex statistical questions about quantities with complex causal dependencies and confounding variables. By using structural models to represent causal relations, the mathematical framework of Structural Causal Models (SCM) can be used to determine the computability of causal questions, to provide answers to these questions when possible, and to determine what assumptions or data is required to answer those which are unanswerable.

Related Pages

Causal analysis extends standard statistical methods, relying on exact inference to model relationships between variables.

Content

Structural Causal Models

Statistical questions about the real world are often causal: they require knowledge of a data-generating process, and cannot be determined from available data directly. Questions about the efficacy of an environmental policy, for example, rely on knowledge of confounding variables such as the price of fossil fuel, public transport funding, cultural attitudes and more. To answer causal questions in a quantitative way, a mathematical framework is needed which is capable of modelling these questions. The mathematical tools of statistics alone do not suffice, as they cannot model questions of cause and effect, only associational relationships.

Any framework used to represent causal expressions should be able to cope with untested assumptions, model causal effect, and answer questions about counterfactuals. Structural Causal Models (SCM) is a framework well suited to representing such causal questions using graphical models.

Causal Expressions

Causal expression can be represented in several ways. In short form, the expression $Y_{x}(u)$ represents the variable $Y$given $u$, subject to variable $X$ being held at $x$. This can be used to represent the probability that the random variable $Y_{x}$ gives value $y$, as $P(Y_{x}=y)$. Alternatively, this can be represented in do-calculus form, $P(Y=y|do(X=x))$, representing the probability that $Y=y$ occurs if $X=x$ is enforced.

Defining Graphical Models

Graphical models provide a straightforward representation of causal relations. In SCM, two types of variables are present: exogenous variables, which represent background factors that are left unexplained, and endogenous variables, which are observable. In path diagram representations, causal relations are represented by directed arrows from cause to effect. An arrow from an unobserved exogenous variable to an endogenous variable is dashed, whereas arrows between endogenous variables are solid. If correlation is possible, it is represented as a dashed double arrow: missing dashed arcs are encoded as independencies.

An example of a structural model $M$ and associated path diagram is as follows; given exogenous variables $U_{Z},U_{X},U_{Z}$and endogenous variables $Z,X,Y$a structural model can be defined by the system of equations,

${\begin{array}{lcl}z=f_{Z}(u_{Z})\\x=f_{X}(z,u_{X})\\y=f_{Y}(x,u_{Y}).\end{array}}$

The path diagram associated with this model is thus represented by graph (a) below.

Advantages of Graphical Models, d-Separation

Graphical models are particularly useful for posing questions about causality, as these have a clear association with the structure of the model. The concept of d-separation is a clear example of this. A set $S$of nodes is said to block a path $p$, where a path is any consecutive sequence of edges in the path diagram, if $p$ includes at least one arrow-emitting node in $S$, or $p$includes one node that is neither in $S$nor a descendant of any node in $S$.

If $S$ blocks all paths from $X$to $Y$, it d-separates them, and they are independent given $S$; that is, $X$⫫ $Y|S.$These conditional independencies are very useful, as they can be used to determine testable implications in the model. In model $M$, for example, the path from $U_{Z}$to $Y$is blocked by $S={X}$, and so $U_{Z}$⫫ $Y|X.$For more complex causal problems with empirical applications, this is an important tool to identify statistical tests which can conclusively prove or disprove a hypothesis under explicitly defined assumptions.

Do-Calculus and Intervention

To answer causal questions regarding specific variables in a model, a technique called intervention is used. This is done by holding the value of specific variables constant, and posing questions about the system subject to those conditions, using the $do$operator: deleting functions from the model and replacing them with a constant. Applying this operator to the previous model $M$ by changing value of $x$ to $x=do(x_{0})$gives the modified model $M_{x_{0}}$, with path diagram (b) and functional representation

${\begin{array}{lcl}z=f_{Z}(u_{Z})\\x=x_{0}\\y=f_{Y}(x,u_{Y}).\end{array}}$

Posing questions about a model subject to intervention is straightforward. For any distribution given by the original model, the new distribution given by the modified model is given by

$P_{M_{x}}(y)\triangleq P_{M}(y|do(x))=\sum _{z}P_{M}(z,y|do(x)).$

Determining Identifiability

It is not always obvious if a given query $Q$ can be made over a causal model when variables in the model and are left unmeasured. The question of whether or not this is possible is called identifiability; when the query is identifiable, it can be estimated from the partially specified model and data under consideration. Given assumptions $A$, a quantity $Q$is identifiable if, for any two models $M_{1},M_{2}$ that satisfy $A$, $P(M_{1})=P(M_{2})\Rightarrow Q(M_{1})=Q(M_{2})$. Once again using model $M_{x_{0}}$as an example, it can be shown that $P(y|do(x))=P(y|x)$is identifiable. This is because $Y$depends only on $X$and $U_{Y}$, and $U_{Y}$is independent of $\{U_{X},U_{Z}\}$, and therefore also independent of $X$.

There are a number of different criterion which can be used to establish the identifiability of a query. One method is as follows: the causal effect $P(y|do(x))$ is identifiable if every path between $X$and any of its children traces at least one arrow emanating from a measured variable. Although this method is sufficient for identification, it is not guaranteed to prove identifiability.

In general, a series of insertion, deletion and exchange operations can be performed on the graph nodes of more complex models to conclusively determine the identifiability of a query given a set of assumptions. This is accomplished by testing if nodes are d-seperable and simplifying the graph and the query until no $do$operator remains in its expression. If this is possible, it can be shown that the query is identifiable; if this is not possible, then the query is not identifiable and could not be estimated from available data.

Calculating Quantities

Once a model is determined, and data is collected for a sufficient set of variables to determine a given quantity, the process of calculating that quantity is straightforward. With identifiability proven constructively, the query becomes a standard inference problem.

To Add

Put links and content here to be added. This does not need to be organized, and will not be graded as part of the page. If you find something that might be useful for a page, feel free to put it here.

Should have been finished already, but may need until end of day.

TODO: describe insertion/deletion/exchange operations for identifiability, add examples

TODO: add clear connections between subsections, reorganize, add discussion-like elements.

TODO: connect concepts to empirical experimentation more directly: what a model corresponds to, what variables correspond to, etc.