Course:CPSC522/Transfer Learning with Markov Logic

Transfer Learning with Markov Logic

Transfer learning, the improvement of learning in a new task due to knowledge transferred from a previous (related) task, with Markov Logic Networks and second-order Markov logic allow learning systems to be more efficient.

Principal Author: May Young

Abstract

This page first covers some background on transfer learning and Markov logic networks. Then it examines two research papers about transfer learning and Markov logic, one about shallow transfer and the other about deep transfer, followed by a comparison and conclusion.

The two papers discussed in this page are:

• Transfer Learning with Markov Logic. Link: http://www.cs.utexas.edu/~ml/papers/tl-icml-wkshp-06.pdf
• Deep Transfer via Second-Order Markov Logic. Link: https://dl.acm.org/citation.cfm?id=1553402

Builds on

This page builds on Markov logic, Markov logic networks, second-order Markov logic, and transfer learning.

Related Pages

Related pages consist of Markov Logic, Higher Order Logic, and Transfer Learning.

Content

Background

Humans have the ability to transfer knowledge between tasks, whether it be between similar or different domains. On the other hand, traditional machine learning algorithms only address isolated tasks, thereby learning each new task from scratch. Obviously, if the domains are related or structurally similar, this approach would waste both data and computer time. Transfer learning attempts to address this gap between humans and learning systems by leveraging previous knowledge in order to improve the efficiency and accuracy of learning a new related task while explicitly assuming that the source and target problems are different. For more information about transfer learning, please see the paper in the "To Add" section below (also linked here).

A Markov Logic Network (MLN) is a combination of first-order logic and Markov networks. More specifically, an MLN is a first-order knowledge base (KB) where each formula has a weight, and provides a model for the joint distribution of a set of variables. An MLN, $L$, acts as a template for constructing a fully-grounded Markov network with a finite set of constants by including a binary node for each grounding of each predicate in $L$, and a feature/factor for each grounding of each formula/clause in $L$. The value of a node is given by the truth value of the corresponding ground literal; similarly, the value of a feature is 1 if the ground formula is true, and 0 otherwise.

Paper 1: Mihalkova and Mooney. Transfer Learning with Markov Logic Networks

The main contribution of the paper is a new MLN transfer learning algorithm that diagnoses the source MLN and updates only inaccurate clauses , decreasing the search space and learning time, while still maintaining the accuracy at the level of the state-of-the-art MLN structure learning algorithm, Alchemy.

The algorithm introduced by Kok and Domingos for MLN structure learning can start from an empty MLN or from a previously-constructed one, i.e. an existing KB. Candidate clauses are generated from considering all possible additions and deletions of literals to existing clauses, as well as all possible sign flips. These candidates are scored using a weighted pseudo-log-likelihood (WPLL) measure. The beam search strategy version of the algorithm is implemented in Alchemy, an open source software package for statistical relational learning and probabilistic logic inference based on the Markov logic representation. Beam search is a greedy version of best-first search and faster than the alternative search strategy, shortest-first search . At the time that the paper was written in 2006, Alchemy was the state-of-the-art structure learning algorithm, which can also be used for transfer. However, one of its limitations is that it does not explicitly attempt to assess or take advantage of similarities between tasks, resulting in an unnecessarily larger search space and longer runtime.

In this paper, the authors propose a new algorithm, TransferNew, for transfer learning of MLN structure that exploits the similarities between tasks after diagnosing the source MLN. It focuses on learning only the inaccurate parts. As a result, it significantly decreases both the learning time and the number of hypotheses considered, while maintaining a level of learning accuracy akin to that of Alchemy.

The learner is given the MLN from the source domain as well as a mapping from the predicates in the source domain to those in the target domain. In addition, the authors assume that the formulas of the given source MLN are disjunctions of literals. Because the learner does not know which parts of the source MLN are useful for the new task and which may need to be relearned, the TransferNew algorithm first diagnoses this network to be able to focus the search for new formulas to the parts of the MLN that actually need to be updated.

The TransferNew algorithm follows two steps:

1. Self-Diagnosis: Inspect the given MLN and determine whether each formula is too general, too specific, or requires no change.
2. Structure Update: Carry out the updates to the clauses by the clauses marked as too general in Step 1 and, similarly, generalizing too specific ones.

Self-Diagnosis

The authors decided to adopt an approach to self-diagnosis that is similar to FORTE’s [cited in ] where the algorithm attempts to prove positive examples in the data. The learner’s inputs are a source MLN and a relational dataset. One of the predicates, say $T$, is the target. To do inference with $T$ as the query predicate whose groundings have their values set to unknown, while evidence is given by the values of all other predicate groundings in the data, the algorithm performs Gibbs sampling with the addition of an extra step. In every round of sampling, it not only recomputes the probability of a ground literal $X$ given its Markov Blanket but also considers all clauses in which $X$ is a member. Each clause $C$ that $X$ participates in can be placed in one of the following four bins.

• [Applies;Good] $C$ is true only when $X$ is true.
• [Applies;Bad] $C$ is true only when $X$ is false.
• [Does not apply;Good] $C$ is true regardless of the value of $X$.
• [Does not apply;Bad] $C$ is trivially true (and $X$ is true).

Hence, in each iteration of Gibbs sampling, the algorithm keeps count of the number of times a particular clause falls into each bin. If the clause was placed in the [Applies;Bad] bin more than $p$ percent of the time, it is marked for specialization. But if the clause fell in the [Does not apply;Bad] bin more than $p$ percent of the time, it is marked for generalization. The authors set the value of $p$ to 10%.

Take, for example (adapted from Mihalkova and Mooney ), the following relational database: $\{Student(Zoe),\neg HasJob(Zoe),Sociable(Zoe)\}$ where the target predicate $T=Student$ and a ground literal $X=Student(Zoe)$. Let $Student(Zoe)=true$.

• $\neg Sociable(Zoe)\vee \neg Student(Zoe)$ is in bin [Applies;Bad] because $\neg Sociable(Zoe)$ is always false (since $Sociable(Zoe)$ is true in the knowledge base (KB)); hence, the clause is true only when $X$, i.e. $Student(Zoe)$, is false, thereby making $\neg Student(Zoe)$ true. This clause is then marked for specialization.

• $\neg HasJob(Zoe)\vee Student(Zoe)$ is in bin [Does not apply;Bad] because the clause is trivially true; both terms are true in the clause. Thus, this clause is marked for generalization.

The self-diagnosis step therefore consists of several iterations where each predicate in the domain is considered as the target.

Structure Updates

Like Alchemy, the TransferNew algorithm also uses beam search starting from the clauses in the previous step, but it only removes literals from too specific clauses and adds literals to too general clauses. These restrictions apply to the candidates produced from a clause as well. Similar to Kok and Domingos, the authors utilize weighted pseudo-log-likelihood to score these candidates [cited in ]. Thus, the search space is reduced by both limiting the number of clauses considered for updates and the kind of update performed on each clause .

Evaluation

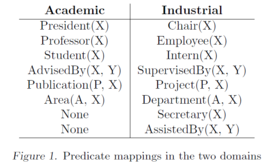
The authors used two synthetic domains: Academic as the source (knowledge about academic departments), and Industrial as the target (analogous knowledge of a company). Please see Figure 1 for predicate examples. Each training example (called a mega-example) in the evaluation represents an organization, contains 50 to 150 true ground literals, and is artificially generated by the authors.

The authors compared the performance of the TransferNew algorithm with ScratchAlchemy (Alchemy starting from scratch) as well as TransferAlchemy (Alchemy starting from the same source MLN given to TransferNew). They used the area under the precision-recall curve (AUC) and the conditional log-likelihood (CLL) as their accuracy metrics. The predicates $supervisedBy$ and $secretary$ were chosen for testing, the former being an interesting relation and the latter being absent in the source domain but present in the target domain.

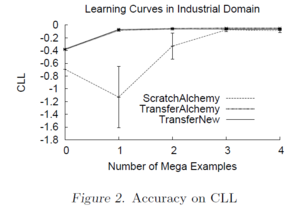
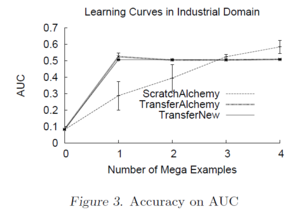
The accuracy of both transfer learning algorithms far exceeds that of ScratchAlchemy (Figures 2 and 3), which demonstrates that the source MLN provides useful information about the target, and that knowledge can and should be transferred.

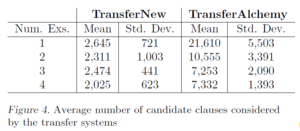
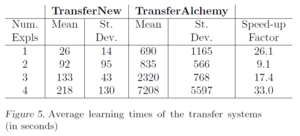
Although the two transfer learning algorithms perform similarly in terms of accuracy, TransferNew has a much lower running time with less variability across training runs (Figure 5). This is because it considers much fewer candidate clauses during beam search than TransferAlchemy (Figure 4). Additionally, this demonstrates the effectiveness of the self-diagnosis step and shows promise that the new algorithm would be well-suited for dynamic environments and situations where quick online relearning is important.

Paper 2: Davis and Domingos. Deep Transfer via Second-Order Markov Logic

The primary contribution of the paper is a new fully automatic approach to transfer learning, called DTM (Deep Transfer via Markov logic) , that addresses the less researched problem of deep transfer: generalizing across different domains. To be able to achieve deep transfer, domain-independent knowledge is important; the authors aim to have it explicit and modular. Most literature in the field of transfer learning look at shallow transfer: generalizing to different distributions over the same variables, or different variations of the same domain .

Although the formulas in an MLN do capture regularities, it only holds for the data in a certain domain; in other words, the knowledge represented by formulas is specific to the types of objects and predicates in a particular domain. Therefore, deep transfer attempts to generalize learned knowledge across domains with different types of objects and predicates. The authors’ approach, DTM, abstracts away domain descriptions via second-order Markov logic [cited by ], where formulas contain predicate variables. The predicate variables are necessary to express domain-independent knowledge and can then model common structures among first-order formulas. It is important to note that DTM makes the assumption that the target domain shares some second-order structure with the source domain.

To give a concrete example of how predicate variables allow DTM to represent structural regularities in a domain-independent way, which is the key intuition behind DTM, consider the two formulas:

$Complex(z,y)\wedge Interacts(x,z)\Rightarrow Complex(x,y)$
$Location(z,y)\wedge Interacts(x,z)\Rightarrow Location(x,y)$

Both are instantiations of the same formula albeit with predicate variables: $r(z,y)\wedge s(x,z)\Rightarrow r(x,y)$, where $r$ and $s$ are predicate variables. Hence, the knowledge can be transferred to another problem and/or domain, where the formulas are instantiated with the appropriate predicate names.

Deep Transfer via Markov logic (DTM)

The basic procedure that DTM follows is outlined below. The input is a set of first-order formulas.

1. Convert each first-order formula into second-order Markov logic by replacing all predicate names with predicate variables.
2. Group the second-order formulas into cliques. Two formulas are in the same clique if and only if they are over the same set of literals.
3. Evaluate “which second-order cliques represent regularities whose probability deviates significantly from independence among their subcliques” . This is to choose cliques that may potentially transfer to the target domain.
4. Select the top k highest-scoring second-order cliques to transfer to the target domain (knowledge transfer).

The authors investigated three ways to reapply the transferred knowledge in the target domain:

1. Transfer by Seeding the Beam (SEED): Recall that beam search maintains a beam of best clauses. At the beginning of each iteration of beam search, DTM seeds the beam with clauses from every legal clique instantiation in the target domain, where “legal” means that the instantiation must conform to the type constraints of the domain. The advantage of this approach is that it forces certain clauses to be evaluated that would not have been evaluated otherwise in a greedy search.
2. Greedy Transfer without Refinement (GREEDY): This strategy does a structure search on only the transferred clauses. It evaluates all clauses and greedily picks the one that would have the greatest improvement in WPLL.
3. Greedy Transfer with Refinement (REFINE): This approach seeds the MLN search with the MLN generated by the greedy procedure described in #2 above, so it can refine the chosen clauses to better match the target domain.

Evaluation

The authors compared the DTM algorithm to the Markov logic structure learning (MSL) algorithm and to TAMAR . MSL is available in the Alchemy software package. Due to the brevity of the section in which the authors discussed TAMAR, it is excluded from further discussion in this page.

The authors used four different domains for their empirical evaluation: Yeast Protein (data on protein location, class, function, interactions, etc.); WebKB (labeled webpages from the computer science departments of four universities); and Social Network (pages from Facebook with information about friendships and properties of individuals, such as hobbies and interests). DTM successfully discovers and transfers relevant information, shown by the fact that it highly ranks second-order cliques that represent several very useful properties including homophily, transitivity, and symmetry. For example, DTM ranks ${r(x,y),r(z,y),s(x,z)}$ first in all three domains examined, which is significant because this represents the concept of homophily. Thus, it makes sense to transfer knowledge about the related objects, x and z, with similar properties y.

The metrics used in the authors’ evaluation of DTM consisted of the test set conditional log-likelihood (CLL) and area under the precision-recall curve (AUC) for each predicate.

Figure 6. Learning curves for the Function predicate when transferring from the WebKB domain

Figure 7. Learning curves for the Linked predicate when transferring from the Facebook domain

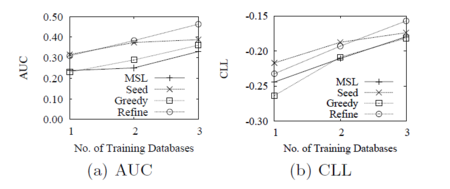
The first experiment was to predict protein function (the $Function$ predicate) when transferring cliques of up to length four from the WebKB domain into the Yeast domain. In Figure 6, it can be seen that DTM outperforms MSL. On the other hand, there is no performance advantage when it is Facebook to Yeast Protein since the cliques transferred are more about link structure and properties of individuals, while in the Yeast domain, similarities and differences in the properties of related entities are more important. Furthermore, MSL outperforms DTM in terms of predicting the $Interaction$ predicate for the same two source-target pairs: WebKB to Yeast Protein, and Facebook to Yeast Protein.

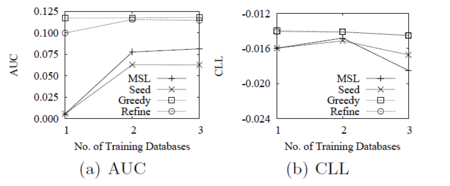
Another experiment was to predict whether two webpages are linked when transferring cliques of up to length four from the Facebook domain into the WebKB domain. Please refer to Figure 7. Again, DTM outperforms MSL, winning 71% of the time. However, when using Yeast as the source, transferring only has a slight benefit, winning only 51% of the time.

Comparison and Conclusion

Both papers address transfer learning with Markov logic. Transfer learning can result in smarter algorithms and significant benefits in terms of performance and efficiency. On the one hand, the first paper addresses the issue of shallow transfer while the second paper addresses the issue of deep transfer.

Markov logic is a powerful formalism that combines logic representation and probabilistic reasoning, resulting in a model that’s both expressive and flexible. It is an important AI algorithm that has many various applications, such as entity resolution and video activity analysis . Therefore, being able to obtain a good, accurate Markov Logic Network is crucial.

The first paper proposes a new MLN transfer learning algorithm that decreases both the search space and the learning time, resulting in a faster and more efficient algorithm, while still maintaining the relatively high level of accuracy of the state-of-the-art MLN structure learning algorithm, Alchemy. Mihalkova and Mooney’s TransferNew algorithm achieved this by taking advantage of previous knowledge, diagnosing the source MLN, and updating only the inaccurate clauses.

The second paper takes it a step further with a different approach to transfer learning, called DTM. Decades of research have produced many sophisticated techniques for solving the task of generalizing from training data to test data from the same distribution, including the one covered in the first paper. However, in real applications, training and test data often come from different distributions. Humans are able to cope with this problem significantly better than machines. Davis and Domingos devised a well-founded, fully automatic approach to deep transfer, which generalizes across different domains, types of objects and variables, and distributions. DTM detects high-level, domain-independent similarities between logical formulas via second-order Markov logic, and uses them to discover new structure in the target domain. As long as the domains are still somehow structurally related, DTM is a promising solution that brings artificial intelligence one step closer to humans.

To Add

Transfer Learning paper: ftp://ftp.cs.wisc.edu/machine-learning/shavlik-group/torrey.handbook09.pdf