Course:CPSC522/Password cracking using PCFGs and Neural Networks

Password cracking using PCFGs and Neural Networks

A comparison of two password-cracking techniques, Probabilistic Context-Free Grammar password-cracking, and neural network password-cracking.

Principal Author: David Johnson
Collaborators:

Paper 1: Password Cracking Using Probabilistic Context-Free Grammars by Matt Weir, Sudhir Aggarwal, Breno de Medeiros, Bill Glodek
Paper 2: Fast, Lean, and Accurate: Modeling Password Guessability Using Neural Networks by William Melicher, Blase Ur, Sean M. Segreti, Saranga Komanduri, Lujo Bauer, Nicolas Christin, and Lorrie Faith Cranor

Abstract

This page looks at two related research papers, the second of which builds on the work done in the first. The first paper discussed is Password Cracking Using Probabilistic Context-Free Grammars by Weir et al. which looks at whether or not Probabilistic Context-Free Grammars can be used to improve on the results of publicly available password-cracking tools. The second is Fast, Lean, and Accurate: Modeling Password Guessability Using Neural Networks by Melicher et al. which compares password-cracking using neural networks to previous methods such as the Probabilistic Context-Free Grammar approach seen in the first paper. This page summarizes both papers and hopes to give an idea of how research has progressed within this field.

Builds on

This page relies heavily on knowledge of Probabilistic Context-Free Grammars and neural networks, specifically recurrent neural networks. It's assumed that the reader has a general understanding of how these two techniques work.

Content

Introduction

Although at first glance it may seem like password cracking research is only leading toward malicious ends, there are many important reasons for which to explore password cracking. For example, it’s important for administrators to pro-actively attempt to crack passwords in their own systems to judge their system’s vulnerability to attack. Password-strength indicators for users, built on password cracking techniques, can be useful tools to demonstrate to users which sort of passwords are secure and which aren’t, helping to better secure users from attacks. Password cracking can also be essential in data recovery such as in cases in which important data is encrypted with a password-wrapped key.

The two papers discussed on this page look at two possible techniques for cracking passwords, both created with the intention of reducing the number of guesses required to crack a password in comparison with other proposed techniques as well as publicly available cracking software such as John the Ripper. The first paper, Password Cracking using Probabilistic Context-Free Grammars by Weir et al., proposes to use Probabilistic Context Free Grammars (PCFGs) as a method for cracking passwords. The second, Fast, Lean, and Accurate: Modeling Password Guessability Using Neural Networks by Melicher et al., instead proposes using a neural network based architecture.

Background

Often when attackers intend to crack a password, they are working on a hashed version of a password, typically stolen from a database of passwords. Their goal is then to use some method of guessing a password which they then hash and attempt to match up with the hashed version of the stolen password. There are typically two guessing approaches used: brute-force and dictionary attacks.

Brute Force: Brute force attacks are done by simply searching every possible combination from the entire password space. While this is theoretically guaranteed to succeed, it’s also very often infeasible to search the entire password space.

Dictionary attack: Dictionary attacks are attacks that draw words from a collection of words (ie. dictionaries) which are expected to be common sources for users to choose passwords. Often when using a dictionary attack, an attacker will apply "word-mangling" rules to words from a dictionary. Word-mangling rules are rules intended to imitate how users typically modify a word in hopes of making their password more secure. For example, if a user's password is "password" they may try to make their password more secure by appending a 1 to the end the word, giving them the password of "password1".

It’s very important to select the right word-mangling rule since each application of the rule will result in additional required guesses. Weir et al. demonstrate this challenge: “For example, adding a two-digit number to the end of a dictionary word for a dictionary size of 800,000 words would result in 80,000,000 guesses. Changing the first letter to be both uppercase and lowercase would double this figure.” Since the choice of word-mangling rules can so greatly impact the number of required guesses, it’s very important to determine which rules will be most likely to simultaneously limit the number of guesses while still resulting in a successful guess.

Password Cracking Using Probabilistic Context-Free Grammars

Introduction

Figure 1. This is a list of the different possible type of strings

Figure 2. This is a list of the different type of grammar structures

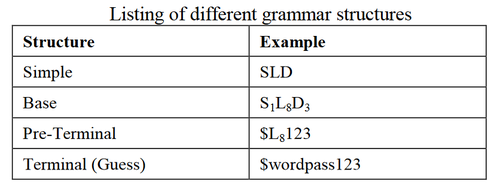
The goal of this form of probabilistic cracking is to limit the number of password guesses as much as possible in hopes of decreasing space and time requirements. In general, the concept is to generate password guesses in decreasing order of probability as determined by the use of a PCFG to maximize the chance of guessing the correct password.

Weir et al. introduce some terminology which they use to describe their method of using PCFGs:

• Alpha string: a sequence of alphabet symbols
  
• Digit string: a sequence of digits
  
• Special string: a sequence of non-alpha and non-digit strings
  

• Alpha strings are denoted as L
  
• Digit strings are denoted as D
  
• Special strings are denoted as S
  

Therefore, a password such as “$password123” is denoted as S₁L₈D₃ as in Figure 1. and Figure 2. The denotation S₁L₈D₃ is referred to as a “base structure”.

Pre-Processing

Pre-processing begins by first deriving all possible observed base structures of all passwords in the training set and the associated probabilities of occurrence. Next, the probability of digits and special strings that appear in the training set is obtained. The probability of alpha strings are not observed from the training set, since the set of possible alpha strings is far larger than what could be observed from a training set.

Probabilistic Context-Free Grammars

Figure 3. This is a partial probabilistic context-free grammar detailing some of the rules allowing calculation of the probability of a pre-terminal structure.

PCFGs are extensions of Context Free Grammars often used for language tasks such as disambiguation or modeling. PCFGs are composed of sets of rules and probabilities which show the probability that the left side of the rule expands into the right side of the rule. Thinking about this in terms of a parse tree for a sentence, the joint probability of a parse T, and sentence S, is the product over the probabilities of all the rule expansions of the right-hand-side (RHS) given the left-hand-side (LHS):

$P(T,S)=\prod _{i=1}^{n}P(RHS_{i}|LHS_{i})$

PCFGs can also be used for language modeling, in which the probability of a sentence can be determined by summing over all probabilities of a parse tree:

$P(S)=\sum _{Ts.t.S=yield(T)}P(T,S)$

For more information on PCFGs, see CPSC522/PCFG

Using Probabilistic Grammars

Figure 4. This is a partial tree which shows the process of generating the "next" pre-terminal structure.

Once the probabilities of base structures and digit/special strings are obtained, PCFGs can be used to derive the probabilities of what are referred to as “pre-terminal structures”: base structures with specific values filled in for D and S. An example grammar is shown in Figure 3. Given this grammar, a possible pre-terminal structure would be S → L₃D₁S₁ → L₃4S₁ → L₃4! with the probability of 0.0975. This pre-terminal structure gives a mangling rule to use with alpha strings from dictionaries in cracking attempts. So, in this case, we would take the mangling rule that alpha strings of length 3, obtained from a dictionary, should be mangled by adding 4! to the end of the word. Once the alpha strings are filled in to the pre-terminal structures, they are referred to as “terminal structures”. These terminal structures, which are the actual guesses for the password, can then be hashed after which point the hash would attempt to be matched to the target password. For example, if the pre-terminal structure is L₃4! and the dictionary is composed of the words {cat, hat, stuff, monkey} then two terminal structures could be generated as {cat4!, hat4!} since they are the strings of length 3 from the dictionary. In this case, cat4! And hat4! would be the possible guesses for the password. These guesses can be hashed and tested for a match with the hash of the actual password.

Weir et al. suggest that this could be done in a distributed process, with one control server computing the pre-terminal structures, then passing the structures to a distributed server that fills in the dictionary word and hashes the guesses.

There are two main ways to choose how to fill in the dictionary words into the pre-terminal structures: pre-terminal probability order or terminal probability order.

Pre-terminal probability order:

In this method, PCFGs are simply used to calculate the highest probability pre-terminal structure, at which point all dictionary words that fit the required length are fit to the pre-terminal structure and tested. Then, the next highest probability pre-terminal is fit with dictionary words of relevant length, etc. This does not assign any probabilities to the alpha strings.

Terminal probability order:

In this method we are able to attain a probability for each individual terminal structure. This builds on the pre-terminal probability order by also assigning probabilities to alpha strings from the dictionary. For example, if there are 10 words of length 3 in the dictionary then each word has a probability of 0.10. This allows the PCFG to be extended to include terminal strings. We end up with a terminal structure (ie. the actual password guess) having a defined probability.

Generating Guesses with a “Next” Function

Figure 7. Pseudocode for the "Next" function.

As stated previously, the original goal is not just to find the correct password, but also to do it in the lowest number of possible guesses. To accomplish this, we would like to optimize running time of our algorithm for generating guesses. So while it would be easy to output all possible pre-terminal structures and rank each of them by their probability, it is not very feasible to parallelize with the distributed password cracking step. Weir et al. present a method that operates in an “online mode” by calculating only the current highest probability pre-terminal structure, given the last output value, and outputting it to the distributed password cracker. For instance, in Figure 4 we see pre-terminals for L₃4! as well as for L₃5! and L₃4%. We would like to calculate and predict L₃4! first, as it has a higher probability, and only if it is not a match will we move to calculating the next nodes L₃5! And L₃4%. To accomplish this, we track a “pivot value” as seen in Figure 4. The pivot value works by indicating which index in the base structure can be changed as we move further down the tree. We are only able to change a part of the base structure if it’s greater than or equal to the pivot value. For example, with node 2 in Figure 4 we see the pre-terminal structure is L₃4! and the pivot value is 0. Since all indices are greater than or equal to this, we can change any index of the pre-terminal structure as we generate children for the parent node. At node 7 we see the pre-terminal structure L₃5! and we see that the pivot value is 1. As we move further down the tree with a pivot of 1 (after checking that node 7 was a match and discovering that it was not) we can change values from index 1 or greater, ie. if looking at L₃5!, L₃ is index 0, 5 is index 1, and ! is index 2. Therefore children of L₃5! Could replace either 5 or ! in the child’s pre-terminal structure which we see with its two children L₃6! And L₃5%

The function that carries out this process is referred to as the "Next" function. Psuedocode for the "Next" function is shown in Figure 7.

Results

Figure 5. This shows the results of comparing pre-terminal and terminal probability methods against John the Ripper.

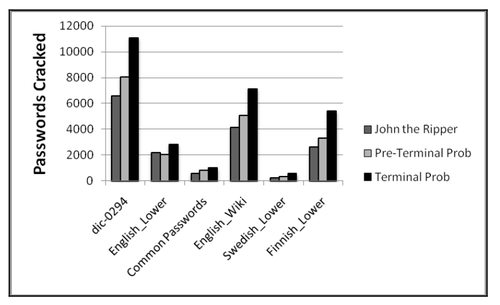
As shown in Figure 5, the PCFG technique is compared to John the Ripper, a publicly available password-cracking tool, in which the comparison is on which technique cracks more passwords in the same amount of guesses. Both PCFG techniques, pre-terminal and terminal, were compared with the default ruleset of John the Ripper. There were 5 different input dictionaries used for both PCFG techniques as well as John the Ripper.

The 5 dictionaries were:

• Dic-0294: an input dictionary obtained from a popular password-cracking website
  
• English_wiki: based on English words obtained from www.wiktionary.org
  
• English_lower: obtained from John the Ripper’s website
  
• Finnish_lower: obtained from John the Ripper’s website
  
• Swedish_lower: obtained from John the Ripper’s website
  
• Common_Passwords: obtained from John the Ripper’s website
  

Both methods outperform John the Ripper, ranging from 28% to 129% more passwords cracked in the same amount of guesses, with the terminal method outperforming the pre-terminal method. These results indicate that PCFGs may be much more effective than common off-the-shelf dictionary attacks.

Fast, Lean, and Accurate: Modeling Password Guessability Using Neural Networks

Introduction

Figure 6. This is an example of a neural network being used to predict 'd' given the context 'ba' and using 4 characters of context. The probabilities of each next character are the output of the network. This also shows post-processing on the output allowing inference of the probabilities of uppercase characters.

Melicher et al.'s paper builds on Weir et al.'s paper using PCFGs to crack passwords but instead uses a neural network architecture. This neural network architecture is intended to be client-side software used to inform users of how strong their password is. Melicher et al. intend to do this by effectively attempting to crack the user’s password, mimicking how a password guessing attack would occur. The more difficult it is to crack the user's password, the stronger the user's password is. They point out that the difficulty is that often attacks such as dictionary attacks can take hours or days of time as well as gigabytes of space, and that this is of course not realistic for a client-side application that needs to give real-time feedback to users.

An additional challenge for Melicher et al. is that they hope to provide a completely client-side application. While it would be easier to have some of the work done server-side, this also potentially ruins some of the security advantages that a strictly client-side application has, since sensitive passwords would have to be sent server-side.

Figure 8. A comparison of performance among multiple techniques measure the percent of passwords guessed as number of guesses increases.

Neural Network Architecture

Figure 9. A comparison of performance among multiple techniques measure the percent of passwords guessed as number of guesses increases.

The solution that Melicher et al. propose is to use a recurrent neural network (RNN). RNNs are a type of neural network often used when dealing with sequential data such as words (letter sequences) since RNNs are able to accept arbitrarily sized sequential inputs. There are different types of specialized RNN architectures used in different circumstances, and for the password cracking task Melicher et al. chose to use a specialized gated RNN architecture called Long Short-Term Memory (LSTM). LSTMs include "memory cells" with gates that determine how much content of a memory cell should be forgotten and how much of the input should be written to memory.

Defined formally:

$s_{j}=R_{LSTM}(s_{j-1},x_{j})=[c_{j};h_{j}]$

$c_{j}=f\odot c_{j-1}+i\odot z$

$h_{j}=o\odot tanh(c_{j})$

$i=\sigma (x_{j}W^{xi}+h_{j-1}W^{hi})$

$f=\sigma (x_{j}W^{xf}+h_{j-1}W^{hf})$

$o=\sigma (x_{j}W^{xo}+h_{j-1}W^{ho})$

$z=tanh(x_{j}W^{xz}+h_{j-1}W^{hz})$

Where s_j is the state at time j which is composed of c_j, the memory component, and h_j, the hidden state component. The input, forget and output gates are denoted as i, f, and o. The candidate for update is denoted z.

For more information on RNNs see CPSC522/Recurrent_Neural_Networks and for LSTMs see LSTM

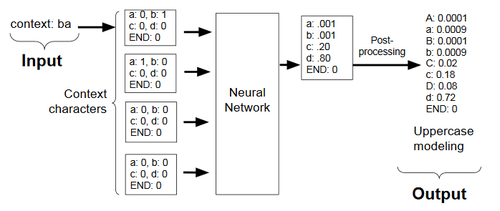
The RNN is used to model character data by predicting what the next character would be in a previous sequence of characters. For instance, if the goal was to predict the password “bad” the RNN would start with an empty string, and then predict the probability of seeing a “b”, then given “b” it would predict the probability of seeing “ba”, and then given “ba” predict the probability of seeing “bad”, and lastly predict the probability of seeing an end flag indicating that “bad” is the password. For each new character prediction the RNN uses the previous 10 characters as “context characters”. In cases in which there are fewer than 10 characters, it pads the input with zeros.

As seen in Figure 6 some character modeling, such as uppercase modeling, is done outside of the RNN with the intention of reducing some of the workload for the RNN. In this sense, the output from the RNN is seen as a template. For example, if the RNN predicts an ‘a’ post-processing can be done to predict ‘a’ and ‘A’. The associated probability of both predictions is determined based on the occurrences of ‘a’ and ‘A’ in the training data.

To generate possible passwords, Melicher et al. “...enumerate all possible passwords whose probability is above a given threshold using a modified beam-search” and then sort the passwords by probability.

Since the goal is to show a user how strong their password is, Melicher et al. propose a method of demonstrating password strength by calculating how many guesses it would take an attacker to guess the user’s password. To calculate these values, a “guess number” is determined. A guess number is “how many guesses it would take an attacker to arrive at that password if guessing passwords in descending order of likelihood.”

Transference Learning

Transference learning is used to train the RNN to take into account the fact that most of the training data comprises passwords that do not fit a password policy and therefore couldn’t actually be possible passwords for a particular policy. For instance, in Melicher et al.'s training set, they have 105 million passwords, but only 2.6 million satisfy a password policy that requires a minimum of 16 characters. If the RNN is trained on a large proportion of passwords which could not possibly be passwords for a given password policy, the RNN is going to generate passwords which are certainly incorrect. Transference learning is a method of training which accounts for this. In transference learning the model is originally trained on all the passwords in the training set. Next, the lower layers of the model are frozen, and the model is retrained on passwords in the training set that fit the policy. Freezing the lower layers of the model is intended to maintain the low-level features that the RNN has learned about passwords, such as “‘a’ is a vowel”, and training the upper layers on just the passwords that fit a specific policy is intended to allow the RNN to learn high-level features such as passwords are typically 8 characters long.

Results

To test their model, Melicher et al. measure how many guesses it takes to crack a password and compare their model with PCFGs, Markov models, John the Ripper, and Hashcat. The data is broken into two sets of training data and five sets of test data. For each of the sets of test data the Melicher et al., “...compute the percentage of passwords that would be cracked after a particular number of guesses. More accurate guessing methods correctly guess a higher percentage of passwords in [the] test set”.

The five test sets used in testing are:

• 1class8: 3,062 passwords longer than eight characters
  
• 1class16: 2,054 passwords longer than sixteen characters
  
• 3class12: 990 passwords that must contain at least three character classes (uppercase, lowercase, symbols, digits) and be at least twelve characters long
  
• 4class8: 2,997 passwords that must contain all four character classes and be at least eight characters long
  
• Webhost: 30,000 passwords randomly sampled from among passwords containing at least eight characters from the 000webhost leak
  

As shown in Figure 8 and in Figure 9, the neural model outperformed all other models as the number of guesses increased for all password types. In particular, we see that the RNN significantly outperformed the PCFG model, which itself outperformed the “off-the-shelf” software of John the Ripper and Hashcat. Figure 8 and Figure 9 also show MinGuess, which is an “idealized guessing approach in which a password is considered guessed as soon as it is guessed by any of [the] guessing approaches” or in other words, if we were able to combine all the guessing methods together into one model that considered a password guessed when any of the methods solved it, we would have the MinGuess. MinGuess indicates that there is value in combining approaches instead of using just a single approach, since different methods guess passwords in different ways.

Ultimately, while there does seem to be a notable improvement in password cracking from the PCFG method proposed by Weir et al. to the RNN method proposed by Melicher et al. there is also certainly some room for further research to improve the capabilities of password cracking with hopes that learning new vulnerabilities can give valuable knowledge to users and administrators of how to keep themselves safe from continually improving attacks.

Annotated Bibliography

1.Bishop, M. Klein, D.. 1995. Improving system security via proactive password checking. Computers and Security. Elsevier Science. Retrieved from https://www.sciencedirect.com/science/article/pii/016740489500003Q
2. Melicher, W., Ur, B., Segreti, S., Komanduri, S., Bauer, L., Christin, N., Cranor, L.. 2016. Fast, Lean, and Accurate: Modeling Password Guessability Using Neural Networks. Proceedings of the 25th USENIX Security Symposium. Retrieved from https://www.usenix.org/system/files/conference/usenixsecurity16/sec16_paper_melicher.pdf
3.Goldberg, Y.. 2017. Neural Network Methods for Natural Language Processing. Morgan & Claypool.
4. Weir, M., Aggarwal, S., de Medeiros, B., Glodek, B.. 2009. Password Cracking using Context-Free Grammars. IEEE. Retrieved from http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=5207658

To Add

Put links and content here to be added. This does not need to be organized, and will not be graded as part of the page. If you find something that might be useful for a page, feel free to put it here.