Maximum Entropy Markov Models (MEMM)

Principal Author: Mehrdad Ghomi
Collaborator: Bahareh Fatemi

Paper 1: Andrew McCallum, Dayne Freitag and Fernando Pereira, Maximum Entropy Markov Models for Information Extraction and Segmentation, 2000.

Paper 2: David S. Rosenberg, Dan Klein and Ben Taskar, Mixture-of-Parents Maximum Entropy Markov Models, 2007

Abstract

This page introduces the Maximum Entropy Model (McCallum et al.) and then builds on it towards another graphical model called Mixture-of-Parents Maximum Entropy Markov Model (Rosenberg et al.). Maximum Entropy Markov Model, also known in the academic literature as MEMM, or MaxEntMM, or Conditional Markov Model (CMM) is a graphical model for sequence labeling. MEMM is a discriminative model (also known as conditional model) meaning that it is a class of models used in machine learning for modeling the dependence of an unobserved variable on an observed variable. Its main domain of application is natural language processing (NLP), especially the tasks of part-of-speech tagging (POS tagging) and Information Extraction. Finally the Mixture-of-Parents maximum entropy Markov model, also known as MoP-MEMM in the literature is presented.

Builds On

MEMM combines the advantageous features of Maximum Entropy (MaxEnt) models with Hidden Markov Models and build on those two^[1]. MEMMs themselves are also not the most efficient models for some NLP domains and tasks such as Named Entity Recognition (NER). The Mixture-of-Parents Maximum Entropy Markov Model (MoP-MEMM) will build on MEMM and make it more ideal to apply to this task. ^[2]

Motivation

There are two main difficulties with the HMMs that motivate the idea of introducing MEMMs which are:
Richer representation for observations: Describing observations with overlapping features is not a possibility with HMMs. These features in the context of NLP can be: Capitalization, word ending, part-of-speech, formatting and position on the page.
Discriminative vs Generative: We want to model the posterior directly to discriminate classes and classify them easily rather than the joint probability of several classes, but this is not a possibility with the HMMs.^[3]
These issues with HMMs motivate to work on a discriminative model that can utilize richer observation presentation.
Moreover, MEMM as a discriminative model that can benefit from more complex and dependent information in the sequential data is not ideal for the tasks that long-range dependencies (nodes that are not adjacent and have a distance between them).^[2]

Content

The content of this page will be split into 3 main parts. First the necessary background knowledge will be discussed. Next will be the introduction of MEMM as the contribution of the first paper, and finally MoP-MEMM will get introduced and analyzed as the contribution of the second paper.

Background Knowledge

It is assumed that the reader of this page knows intermediate level of some topics in mathematics such as: probabilities, distributions and graph theory, as well as some of the machine learning techniques and artificial intelligence algorithms. Also, basic knowledge of natural language processing and its terminologies is a necessity but the immediate background knowledge necessary for understanding the two topics discussed in the papers will be explained briefly.

Hidden Markov Models (HMMs)

Hidden Markov models are assumed to be Markov processes and are statistical Markov models with unobserved hidden states. These models are vastly used in temporal pattern recognition tasks domains such as part-of-speech tagging, bioinformatics, speech, handwriting and gesture. Refer to our course Wiki page regarding this topic for more detailed information by clicking here. Hmms are joint models which maximize the joint probability P(x,y) while there are cases were calculation of the posterior distribution P(y|x) directly is beneficial. Also, the input features are limited to the observations themselves, and cannot use arbitrary features in HMMs.^[4] HMMs cannot benefit from more complex features, such as: word Capitalization, word position in a sentence or paragraph in many NLP tasks such as POS tagging and NER. ^[3]

Three Classical Problems of HMMs

Evaluation problem: Given an HMM, determining the probability of a given observation sequence.

P({\overline {o}})=\sum _{\overline {s}}P({\overline {o}}|{\overline {s}})P({\overline {s}})

Decoding problem: Given a model and an observation sequence, determining the most likely states that led to the observation sequence.

\arg \max P({\overline {o}}|{\overline {s}})

Learning problem: Suppose we are given the structure of a model (S,O) only. Given a set of observation sequences, determining the best model parameters.

\arg \max P({\overline {o}},\Theta )=\sum _{\overline {s}}P({\overline {o}}|{\overline {s}},\Theta )P({\overline {s}})

Fortunately, efficient Dynamic Programming (DP) algorithms exist that can solve these problems which are: Forward, Viterbi, and Baum-Welch respectively.^[3]

HMMs Assumptions

Markov assumption: the next state depends only on the current state.
Stationarity assumption: state transition probabilities are independent of the actual time at which transitions take place.
Output independence assumption: the current output (observation) is independent of the previous outputs (observations) given the current state.^[3]

Maximum Entropy (MaxEnt)

Maximum entropy probability distributions in statistics aim for maximizing the expected value of information contained in each flow of information. Which is, making sure that this expected value is at least as great as that of all other members of a specified class of probability distributions. These models follow the principle of maximum entropy which states that given that there is no knowledge regarding a distribution other than that is belongs to a certain class, the distribution with the largest entropy will be the least-informative default and should be chosen. If X is a discrete random variable with distribution given by:

\operatorname {Pr} (X=x_{k})=p_{k}\quad {\mbox{ for }}k=1,2,\ldots

then the entropy of X is defined as:

H(X)=-\sum _{k\geq 1}p_{k}\log p_{k}

If X is a continuous random variable with probability density P(x), then the differential entropy of X is defined as:

H(X)=-\int _{-\infty }^{\infty }p(x)\log p(x)dx\;.

Skip-Chain Models

In the MEMM, when the input sequence X is conditioned, the label variables y₁, ...., y_n form a Markov chain. The conditional independence structure of this model is given by a directed graph, with edges connecting adjacent labels. Consider a much more general model, in which additional "skip" edges to connect nonadjacent labels. This model is called a directed skip-chain model. The graphical structure of this model is shown here with the long-range skip edges shown dashed: ^[2]

Figure 1. Directed skip-chain model.
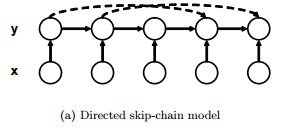
(Source: Rosenberg et al.)

With respect to the graph structure, the parents of a label y_k comprise the label y_k-1 immediately preceding it, as well as any earlier labels connected to y_k via a skip edge. And for the undirected case is:

Figure 2.Skip-chain CRF model
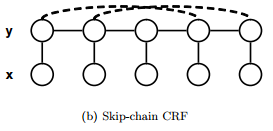
(Source: Rosenberg et al.)

The conditional distribution of y_k is:

p(y_{k}|y_{1},...,y_{k-1},X)=p(y_{k}|y_{\pi _{k}},X)

Where π_k denotes the set of parent labels.

Maximum Entropy Markov Models

(Contribution of the first paper)
MEMM or conditional Markov model (CMM) is a discriminative graphical model for sequence labeling that combines features of HMMs and MaxEnt models. It extends a standard maximum entropy classifier by assuming that the unknown values to be learnt are connected in a Markov chain rather than being conditionally independent of each other.

Model and Algorithm

In MEMMs we model the probability of reaching a state given an observation and the previous state. Given a sequence of observations $O_{1},\dots ,O_{n}$ that we seek to tag with the labels $S_{1},\dots ,S_{n}$ that maximize the conditional probability $P(S_{1},\dots ,S_{n}|O_{1},\dots ,O_{n})$ . In a MEMM, this probability is factored into Markov transition probabilities, where the probability of transitioning to a particular label depends only on the observation at that position and the previous position's label. In these models we have finite number of states and possible observations.
$P(S_{1},\dots ,S_{n}|O_{1},\dots ,O_{n})=\prod _{t=1}^{n}P(S_{t}|S_{t-1},O_{t}).$
Each of these transition probabilities come from the same general distribution $P(s|s',o)$ . For each possible label value of the previous label $s'$ , the probability of a certain label $s$ is modeled in the same way as a maximum entropy classifier.

P(s|s',o)=P_{s'}(s|o)={\frac {1}{Z(o,s')}}\exp \left(\sum _{a}\lambda _{a}f_{a}(o,s)\right).

Legend:
$\lambda _{a}$ are the parameters to be learned.
$f_{x}$ new ordinal-valued "correction" feature where x = n + 1.
$Z(o,s')$ is the normalizing factor that makes the distribution sum to one across all next states s.
$f_{a}(o,s)$ are real-valued or categorical feature-functions.

Training algorithm: 

1) Split the training data into observation - destination state pairs for each state s'.

2) Apply Generalized Iterative Scaling (GIS) (Darroch & Ratcliff et al. 1972) ^[6] for each s' using its state pair set to learn the maximum entropy solution for the transition function of s'.^[3]

MEMM Model overview, please refer to the legend if any part is ambiguous
(Source:"Gyozo Gidofalvi")

Strengths and Weaknesses

An advantage of MEMMs rather than HMMs for sequence tagging is that they offer increased freedom in choosing features to represent observations. In sequence tagging situations, it is useful to use domain knowledge to design special-purpose features. In the original paper introducing MEMMs, the authors write that "when trying to extract previously unseen company names from a newswire article, the identity of a word alone is not very predictive; however, knowing that the word is capitalized, that is a noun, that it is used in an appositive, and that it appears near the top of the article would all be quite predictive (in conjunction with the context provided by the state-transition structure)." ^[1]
Useful sequence tagging features, such as these, are often non-independent. Maximum entropy models do not assume independence between features, but generative observation models used in HMMs do. Therefore, MEMMs allow the user to specify lots of correlated, but informative features. ^[1]
Another advantage of MEMMs versus HMMs and conditional random fields (CRFs) is that training can be considerably more efficient. In HMMs and CRFs, one needs to use some version of the forward-backward algorithm as an inner loop in training. However, in MEMMs, estimating the parameters of the maximum-entropy distributions used for the transition probabilities can be done for each transition distribution in isolation.
A drawback of MEMMs is that they potentially suffer from the "label bias problem," where states with low-entropy transition distributions "effectively ignore their observations." Conditional random fields were designed to overcome this weakness, which had already been recognised in the context of neural network-based Markov models in the early 1990s. Another source of label bias is that training is always done with respect to known previous tags, so the model struggles at test time when there is uncertainty in the previous tag. ^[5]

Results

For the task of Segmentation, the authors have applied their MEMM method to a FAQ dataset and measured segmentation precision (SegPrec) and segmentation recall (SegRecall) and the Co-occurrence agreement probability (COAP). All these averages in the figure below have 95% confidence intervals of 0.01 or less.

Comparison of MEMM_Results with a few other models from the first paper
(Source: "McCallum et al.")

Where: A segment is counted as correct if it has the same boundaries and label (e.g., question) as an actual segment.
The segmentation precision (SP) is the number of correctly identified segments divided by the number of segments predicted.
The segmentation recall (SR) is the number of correctly identified segments divided by the number of actual segments.

Some of the MEMM Applications

Part-of-speech tagging:
In corpus linguistics, part-of-speech tagging (POS tagging or POST), also called grammatical tagging or word-category disambiguation, is the process of marking up a word in a text (corpus) as corresponding to a particular part of speech, based on both its definition and its context—i.e., its relationship with adjacent and related words in a phrase, sentence, or paragraph. As an example:
<PRP>He</PRP> <VB>books</VB> <NNS>tickets</NNS>
Text segmentation and event tracking:
Text segmentation is the process of dividing written text into meaningful units, such as words, sentences, or topics. For instance:
tracking non-rigid motion in video sequences
Named entity recognition:
Named-entity recognition (NER) (also known as entity identification, entity chunking and entity extraction) is a subtask of information extraction that seeks to locate and classify elements in text into pre-defined categories such as the names of persons, organizations, locations, expressions of times, quantities, monetary values, percentages, etc. As an example:
<ORG>Mips</ORG> Vice President <PRS>John Hime</PRS>
Information extraction:
Information extraction (IE) is the task of automatically extracting structured information from unstructured and/or semi-structured machine-readable documents. For example:
After lunch meet <LOC>under the oak tree</LOC>

Other Alternatives

There are various graphical models that are similar to each other in many ways and they differ from others in some certain properties. There is no right model that can be applied to most of the problems optimally. Each of these models perform well on some tasks and poor on others. To name a few of these alternatives:

Hidden Markov Models
Conditional Random Fields (CRFs)
Maximum Entropy Markov Models
Mixture of Parents Maximum Entropy Markov Model

Here is a presentation of the MoP-MEMM model and a Named Entity Recognition task and MoP-MEMM performance for that task are provided.

Mixture-of-Parents Maximum Entropy Markov Models (MoP-MEMM)

(Contribution of the second paper)

Model

A directed skip-chain model is a Mixture-of-Parents model if the expression:

p(y_{k}|y_{1},...,y_{k-1},X)=p(y_{k}|y_{\pi _{k}},X)

can be written as:

p(y_{k}|y_{\pi _{k}},X)=\sum _{j\epsilon \pi _{k}}\alpha _{kj}p(y_{k}|y_{j},X)

where the mixing weights α_kj are positive for each kj
This model can compute the marginal posterior efficiently from the calculations below:

p(y_{k})=p(y_{k}|y_{1},...,y_{k-1})p(y_{1},...,y_{k-1})

=\sum _{j\epsilon \pi _{k}}\sum _{y_{1},...,y_{k-1}}\alpha _{kj}p_{j}(y_{k}|y_{j})p(y_{1},...,y_{k-1})

=\sum _{j\epsilon \pi _{k}}\alpha _{kj}p_{j}(y_{k})

So for a skip-chain mixture of parents model, the posterior distribution of a node y_k is a convex combination of the predictive distributions given by each parent separately.^[2]
We call this model a skip-chain mixture-of-parents model because it defines a probabilistic mixture model. The generative interpretation of such a model is that to generate y_k given the parents we first randomly choose one of the parent labels according to the multinomial probability distribution Then, according to the mixture model, only this parent label is relevant to the determination of the label y_k. For example, if the randomly chosen parent node is y_j, then y_k is drawn according to the conditional probability distribution:

P(y_{k}|y_{j},X).

Learning

The focus is on learning the parameters $\lambda$ and $\mu$ of the local transition models $p_{\lambda ,\mu }(y_{k}|y_{j},x)$ , and the mixing weights $\alpha$ are given by the assumption. In the NER experiments, the authors used a uniform mixing distribution. The standard method for training MEMMs is to maximize the conditional log-likelihood of the data. Under some regularization of the parameters $\lambda$ and $\mu$ . In their experiments, they used ridge regularization, which penalizes the sum of squares of all the weights equally.

The Task and Results

The authors have applied the mixture-of-parents MEMM to the CoNLL 2003 English named entity recognition (NER) dataset, and the WebKB dataset [Craven et al., 1998].
There are several things one must consider when applying a mixture-of-parents MEMM to data. First, although a MEMM may theoretically have a different parameter vector for each edge, in practice this gives too many parameters to estimate from the data. The typical approach is to use the same parameter vectors on multiple edges. In terms of the model description above, the authors have limit the number of distinct maximum-entropy conditional probability distributions that must be learned. ^[2]
They have presented the performance results of several sequence models on the NER test set as a tabular presentation: ^[2]

Comparison of Performances of different models from the second paper. Please refer to the legend for a better understanding of the abbreviations
(Source: "Rosenberg, et al.")

Legend:
F1 = f1 score
FP = False Positive
FN = False Negative

All the comparisons are with the Posterior MEMM

Annotated Bibliography

[1] Andrew McCallum, Dayne Freitag and Fernando Pereira, Maximum Entropy Markov Models for Information Extraction and Segmentation, 2000.
[2] David S. Rosenberg, Dan Klein and Ben Taskar, Mixture-of-Parents Maximum Entropy Markov Models, 2007
[3] Gyozo Gidofalvi, 17th International Conf. on Machine Learning, 2000, MEMM for IE and Segmentation
[4] Xingyuan Pan, CS Structured Prediction Presentation, ICML 2000
[5] Lafferty, John; McCallum, Andrew; Pereira, Fernando (2001). "Conditional Random Fields: Probabilistic Models for Segmenting and Labeling Sequence Data". Proc. ICML 2001.
[6] Darroch, J.N. and Ratcliff, D. (1972). "Generalized iterative scaling for log-linear models". The Annals of Mathematical Statistics (Institute of Mathematical Statistics) 43 (5): 1470–1480.

To Add

Working on Conditional Random Fields (CRFs) and its connections, similarities and differences with the models mentioned above can be an improvement for this page that future contributors can consider.