Course:CPSC522/Learning User Preferences of Motion Control

Title

The goal of this project is to add intervention to a power wheelchair system so that when the user expresses frustration due to limited joystick control abilities, the system can adjust the control to match the users preference.

Principal Author: Ainaz Hajimoradlou, Jocelyn Minns

Content

Problem

Figure 1. Design of a Power Wheelchair. Image source usmedicalsupplies.com

Modern power wheelchairs are an essential tool to many who are mobility challenged. However, while this gives freedom to some who would otherwise be restricted in their day to day life, other users are still limited from safely operating these large, heavy and powerful machines. Users that experience motor and/or cognitive impairments may be be unable to operate a power wheelchair to the accuracy that is required. Most common power wheelchairs are operated using a joystick controller to steer the motors. If the user is unable to perform the small movements for precision control and the large movements to achieve reasonable speed, then they could become frustrated and may compromise their own safety. The goal of this project is to add intervention to the system so that when the user expresses frustration with the control of the power wheelchair, the system can adjust to match the users preference.

Simulated Environment

Figure 2. A simulated holonomic robot exploring the environment.

The most common form of a power wheelchair can be modelled as a differential drive robot. Meaning that the robot has two main wheels attached to the sides of the robot each with its own motor. A wheelchair also contains four caster wheels at the front and back to ensure stability and balance. The caster wheels generally do not effect the motion of the chair since they can rotate freely and are not attached to any motor. Since each of the two main wheel are attached to its own motor, they can rotate in opposite directions or at different velocities allowing the user to turn or even spin in place. This model proposes its own set of challenges in simulation. Accurately mapping the linear and rotational velocities given the user input from the joystick control can be a large problem on its own.

To test our initial approach, it is desirable to start with a simpler model than the one described above. Using a holonomic robot design lifts some of the restrictions of the differential drive design allowing us to easily simulate the movement of the robot. With this design, the robot is free to move in any direction in the x-y plane. We can then focus on the linear velocity only and adapt to the users preferences accordingly.

For our simulation, we are not able to use real power wheelchair users to provide feedback for our system. Instead we simulate users such that each user will have a set level of ability to use the joystick controls and a desired speed that they wish to go. The desired speed remains unknown to the system, the only feedback that the user gives is a verbal description of the speed as too fast or too slow. The joystick controls are fed to the system at 30 Hz, however the user is unable to provide feedback at that rate so there is some delay to the users commands based on the accurate movement of the chair.

Approach

Figure 3. Magnitude of velocity of the user at each time step.

The first models we considered were Markov models such as Markov chains, Hidden Markov Models and Continuous Markov process. Since, obtaining the parameters of each state such as velocity and position depends on previous states. However, we encountered a problem when fitting data with these models due to the nature of the proposed problem. We have to get the feedback from the user in form of verbal complaint, but these models do not support having such inputs. Therefore, we decided to go with a simple version of a baseline model.

Figure 4. A simple robot motion based on the proposed baseline.

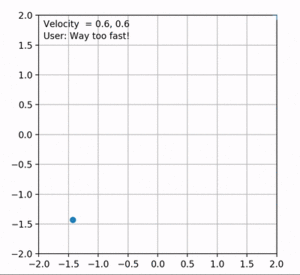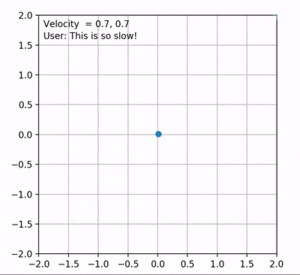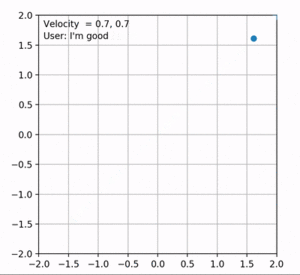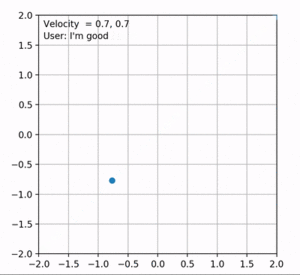
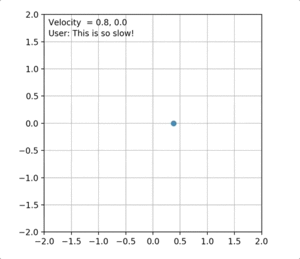
Each state in the model specifies current velocity, position and the direction the user is going with joystick controllers. A desired linear velocity exists which is specified by user as the input to the model. So, based on this linear speed, feedbacks are divided into three categories: fast, good and slow. The model's approach is to start with increasing the velocity until the feedback from the user states that the speed is too fast. The point where this feedback is achieved, high margin of the speed is obtained. Low margin is the previous state's velocity. Based on these margins, the desired speed of the user is obtained by a simple binary search. When the desired speed is achieved, user will give a feedback ("good speed") and the velocity will remain constant until the user's direction changes. So at each time step, based on current velocity and the spent time, the position of the user is updated in the plot. This process will repeat until the user stops or reaches the desired speed. The magnitude of velocity at each time step is plotted in figure 3.

Results

Figure 5. Simple robot motion with different velocities along each axis.

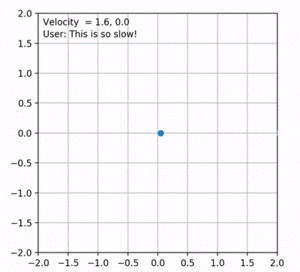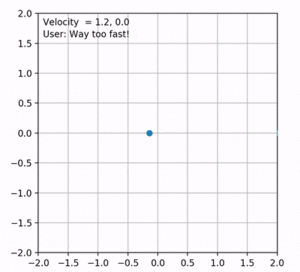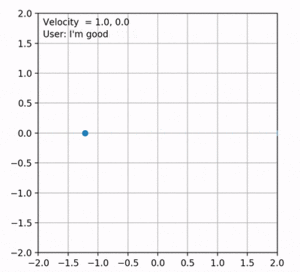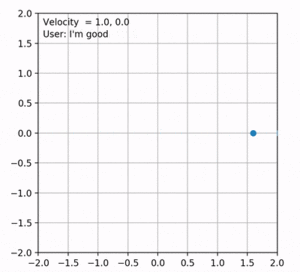
Figure 4 shows an example of the results obtained by the baseline. In this case, the velocities along each axis are increased to the same extent. Therefore, the robot moves in the y = x direction. However, this is not optimal as the robot's direction changes every now and then. Depending on the direction, the velocities should be amplified accordingly. To solve this, we can simply find the angle between current position of the robot and the desired direction which is the goal. Cosine and Sine of this angle will be the multipliers of the velocities in x and y axes. The updated results are shown in figure 5. The direction of the user in this figure is at point (1, 0).

Future Work

Figure 6. A simulated differential drive robot using the RobotPy package.

The two main focuses for future work is to improve the robot design of the power wheelchair and to improve the simulated user. Using a predesigned robot simulator such as RobotPy, we are able to simulate a differential drive robot. However, the mapping of the joystick controller to the movement is highly inaccurate to a real wheelchair system. Power wheelchairs inherently apply some mapping function from the control to the motors to provide the user with safer control. Examples of this is the decreased velocity when backing up or the decreased rotational velocity when spinning in place. To build a mapping of the control to the motors is a non trivial job, but would be necessary to use a more accurate model. Once the model was in place, we would be able to adjust the control to accommodate the users preference for both the linear and rotational velocities.

To improve the simulated user, we would add noise to the users inputs/outputs. The user perception of the velocity would have some variation as well as the users ability to use the joystick control. The user would also want to adjust their desired speed given different environments or different obstacles. Besides, speaking in terms of model, we can smooth the obtained parameters of the state by using moving average instead of finding a desired velocity in the specified margin. To further extend the project we should focus on adapting the model to more complex simulation environments as the one shown in figure 6.