Course:CPSC522/Identity Uncertainty

Identity Uncertainty

Identity uncertainty is the task of deciding whether two descriptions correspond to the same object.

Paper 1: Pasula, H., Marthi, B., Milch, B., Russell, S. and Shpitser, I. (2003). Identity uncertainty and citation matching, NIPS, Vol. 15.

Paper 2: Rita Sharma and David Poole, ``Probability and Equality: A Probabilistic Model of Identity Uncertainty, Eighteenth Canadian Conference on Artificial Intelligence, Victoria, May 2005.

Principal Author: Bahare Fatemi

Collaborator : Mehrdad Ghomi

Abstract

Identity uncertainty is the task or recognizing whether two descriptions refer to the same object or not. It can be applied to different fields. In this page, the application of identity uncertainty in citation matching and person identity uncertainty has been studied. Authors of paper 1 tried to solve identity uncertainty in the context of citation matching. They modeled the dependencies among the records using a relational probabilistic model to recognize whether two citations refer to the same paper or not. The second model solved the problem of person identity uncertainty, where the two descriptions are about people. They model the problem as a Bayesian network. They show that using dependencies among attributes of a person is quite helpful in their task. In this page, an introduction to the identity uncertainty and the models built by the two different groups of authors has been presented and it has been shown how they evaluated their models. At the end, a discussion of the comparisons of the papers has been provided.

Builds on

This page contains an introduction on identity uncertainty. In the background, Bayesian networks and probabilistic relational models are introduced.

Related Pages

The other page discussing identity uncertainty is Record Linkage and identity uncertainty.

Content

Introduction

Identity uncertainty is the task of deciding whether two descriptions correspond to the same object. It is is an extensive problem in real-world analysis whose aim is to recognize records of different files which represent identical people, objects, or events. This problem has been studied independently under various names by different communities. For example, it has been studied as record linkage in statistics, as duplicate detection in , and as merge/purge problem in .

Identity uncertainty has been applied to different problems. Citation matching is one of the challenging problems that identity uncertainty has been successfully applied to. There are different ways of citing a specific paper. Consider a specific paper with a list of citations. It is usually difficult to define which actual papers are cited in the given paper. In addition to different ways of citing papers, there are lots of typing errors, single digit or letter errors, copying errors, and so on. The aim of identity uncertainty for citation matching is to match a given citation to an actual paper.

One other application of identity uncertainty is in merging different databases. Suppose several companies decide to merge and start a bigger company altogether. Each of these companies has a database consisting of their customers’ records. These records contain important information that are of great value for the company, so the databases are required to be merged. Even though customer information might be stored in different ways in different databases, some records in two or more databases may refer to the same customer. The aim of identity uncertainty in this application is to find such records to avoid duplicates and inconsistencies in the final database. This application of identity uncertainty is known as person identification.

Background

Bayesian Belief Networks

A Bayesian network (BN) or belief network is an acyclic directed graph consisting of random variables (corresponding to nodes) whose arcs demonstrate the interdependencies and conditional independencies among random variables. Each random variable in a BN is independent of its non-descendants given values for its parents. So the joint probability of the random variables can be factorized as:

$P(X_{1},X_{2},...,X_{n})=\prod _{i=1}^{n}P(X_{i}|parents(X_{i}))$

Relational Probabilistic Model

Relational probabilistic models (PRMs) or template based models extend Bayesian networks by adding the concepts of individuals. Individuals can be objects, entities, or things. In probabilistic relational models, individuals about which we have the same information are exchangeable, so they are treated identically. A PRM models the uncertainty about the characteristics of the individuals, how the characteristics of one individual influences the characteristics of other individuals, and also the uncertainty about the relationships among the individuals. Probabilistic relational models are built before knowing the actual individuals in the test set. They use one set of individuals for learning and apply what they learn to (possibly) new individuals.

Proposed Solution 1

The Probability Model

The problem of citation matching is to decide whether two (possibly) different citations refer to the same paper or not. As explained earlier, citation matching is an instance of the identity uncertainty problem. In Figure 1, there are two citations that probably refer to the same paper.

The first paper that I read tries to solve the citation matching problem by formulating it as a probabilistic relational model (PRM). The proposed RPM is in Figure 1. In the proposed model, there are four classes of objects: Author, Paper, Citation, and AuthorAsCited which represents the cited authors, not the actual authors. For each citation C1, a new instance of the Citation class is created and its text attribute is set to the text of the citation. Then its paper attribute is set to a newly created paper instance P1. In this work, for simplicity they introduced max(#[author]) as the maximum number of authors that a paper can have in their database and so created max(#[author]) instances of AuthorAsCited. Assuming max(#[author])=3, D11, D12, and D13 are instances of AuthorAsCited (D1i are AuthorAsCited instances for citation C1), which fill the P1.obsAuthors (indicating authors of the paper). Now max([#[author]) instances of the class Author should be created as A11, A12, and A13 (A1i are actual authors of citation C1) to fill P1.authors[i] and D1i.author attributes.

Figure 1: An RPM model explained in the paper.

Now assume the value of C1.parse is observed. Based on this value, the values of basic attributes for Citation and AuthorAsCited can be set. For example in the first citation in figure 1, after a correct parse is observed, D11.surname is set to Lashkari, and D12.fnames is set to Max. There are more basic attributes in Paper and Author instances whose values are unobserved.

In order to do inference in this model, they express the described PRM with a Bayesian network, in which each of the basic attributes in the RPM becomes a node. In the application of citation matching, each of two citations may or may not refer to the same paper and this statement affects the structure of the Bayesian network. As an example, if C1 and C2 refer to two different papers, the Bayesian network will be as in Figure 2 and the two citations have two distinct sets for their basic attributes. But if C1 and C2 refer to the same paper, they share one set of basic attributes. Whether C1 is equivalent to C2 or not affects the number of nodes in the Bayesian network.

Figure 2: The Bayesian network equivalent to the explained RPM, assuming C1 $\neq$ C2.

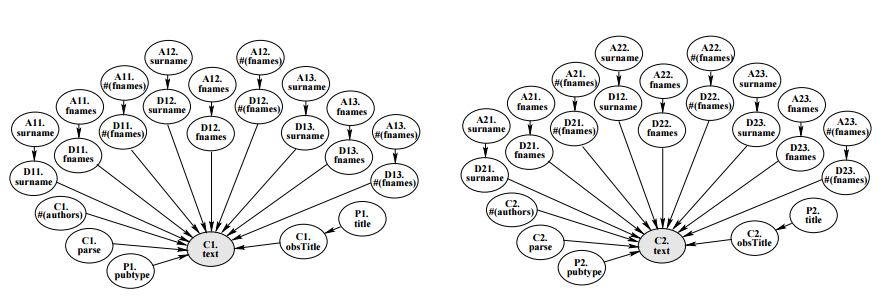
This paper builds the Bayesian network in a way that the network contains not only the basic attributes of instances, but also the number of objects n and an identity clustering $\iota$. $\iota$ is defined as a mapping from the terms in the language to the real objects in the world. In the citation matching problem, we are only interested in whether terms co-refer or not. Consider that $P_{1}$ and $P_{2}$ are the only terms and they co-refer, then $\iota$ = {{$P_{1}$, $P_{2}$}}; if they do not co-refer, then L = {{$P_{1}$}, {$P_{2}$}}.

In order to complete their model, they assume that citations should have unique names assumption. So $P(\iota _{citation})=1$ for the assignment where each citation is unique. But the Paper and Author classes are subject to identity uncertainty. So they specify $P(n)$ using a high-variance log-normal distribution. They assume that prior to obtaining any information, papers are equally likely to be cited, and authors are equally likely to write a paper. According to these assumptions, the probability of an assignment $\iota _{C,k,m}$ that maps k named instances to m distinct objects when C contains n object is given by:

$P(\iota _{C,k,m})={\frac {n!}{(n-m)!}}{\frac {1}{n^{k}}}$

Evaluation

They have applied their proposed method to some hand-made datasets. Each of these datasets contains several hundred citations of machine learning papers. They showed in the table 1 that their algorithm beats the state-of-the-art citation matching algorithm called “phrase matching”.

Table 1: Results of four Citeseer data sets, for the text matching and the proposed PRM

	Face/th>	Reinforcement	Reasoning	Constraint
Phrase matching	94%	79%	86%	89%
PRM	97%	94%	96%	93%

Proposed Solution 2

This paper discussed identity uncertainty problem in the context of person identity uncertainty or person identification: the descriptions are information about people and the uncertainty is about recognizing whether two descriptions are about the same person or not.

This paper proposed a solution based on demographic attributes of people. For each person, they have the following seven attributes: Social insurance number (SIN), first name (Fname), last name (Lname), date of birth (DOB), gender (Gen), phone number (PH), and postal code (PC). This paper presents two hypotheses: record X and record Y denote the same person or not, and separate Bayesian networks are constructed for each hypothesis.

Model for hypothesis of X not equal y

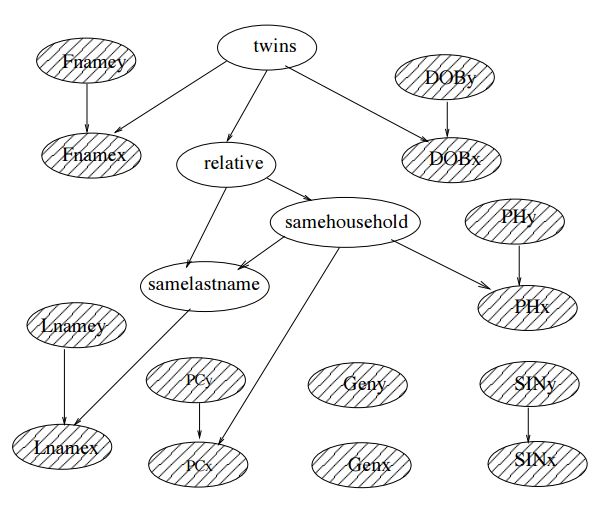
Figure 3 is the proposed model for the hypothesis of record x and record y denote different people. They claim that they model the dependence among the attributes using the known relationship between people. The propositions twins, relative, samehousehold, and samelastname represent that X and Y are twins, relatives, living in the same household, or have the same last name. They assume that the gender of two different people is independent of each other. Attribute SIN does not depend on the other attributes. However, SIN of X is not independent of SIN of Y, because knowing X’s SIN changes our belief about Y’s sin as different people have different SIN. They consider a very very small probability for two people having the same SIN. Shaded nodes in the network of figure 3 are observed nodes.

Figure 3: Similarity network representation of attribute dependency for hypothesis X $\neq$ Y (shadednodes are observed).

Model for hypothesis of X = Y

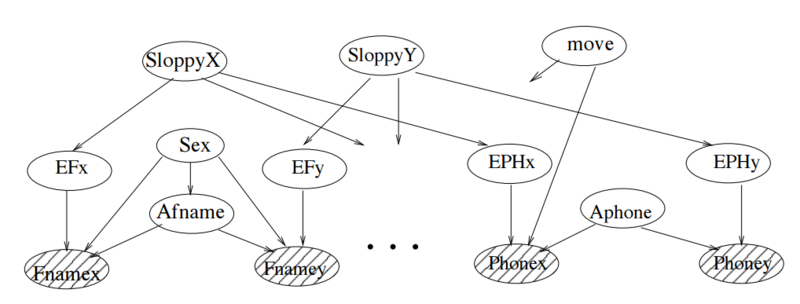
If records X and Y refer to the same person, their attributes should be the same for both X and Y. However, there may be differences because of errors such as typing errors, nicknames, and so on. They consider two cases of attribute dependence: first, the typist could have been sloppy, and second, the person could have moved to a new place of residence. The model for this hypothesis is in Figure 4. Unshaded nodes show the hidden variables, and shaded nodes are observed variables. The proposition Afname represents the actual first name. The proposition move represents the possibility that the person has moved. The proposition EFx represents the error in the first name of record X. They consider the following types of errors in their paper: copy error (ce), an error where a person copies a correct name but from the wrong row of the table, single digit or letter error (sde), or lack of any errors as noerror. Random variables Fnamex, Fnamey, and Afname have the domain of all possible first names.

Figure 4: Similarity network representation of attribute dependency for hypothesis X = Y (shadednodes are observed).

Large conditional probability tables

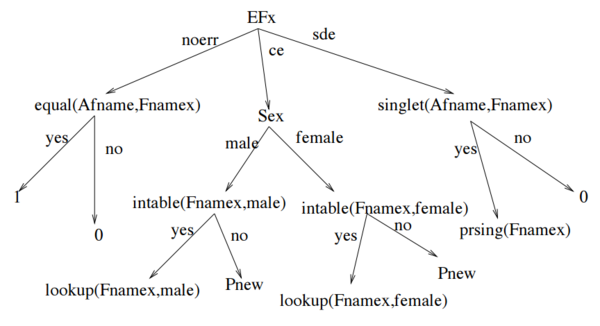
Some of the CPTs in the generated Bayesian network are huge, for example the CPT P(Fnamex|Aname and Sex and EFx). They consider a decision tree representation to solve the problem of storing the large CPTs. Figure 5 shows the decision tree that they used for the CPT P(Fnamex|Aname and Sex and EFx). In this decision tree, predicate equal tests the equality of two inputs, predicate singlet tests whether two inputs are a single letter apart or not, and predicate intable tests whether the first input exists in the table named with second input. The function parsing is used to compute the probability when the data entry person makes the single digit error.

Figure 5: A Decision Tree Representation of the CPT P(Fnamex$|$ Afname ∧ Sex ∧ EFx).

Evaluations

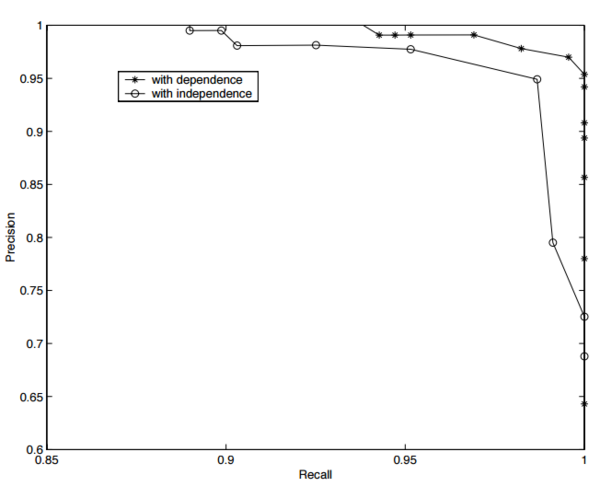
They model a small town of 1500 households. After creating the true populations, they made two datasets, $D_{a}$ and $D_{b}$. To create $D_{a}$, they randomly took 600 records from the true population, they corrupted some of the records by typographical errors. $D_{b}$ dataset is built in the same way as $D_{a}$ but with 1500 records from the true population. They compare each record of dataset $D_{a}$ with each record of dataset $D_{b}$. Figure 6 shows the diagram of recall versus precision for both attribute dependence and attribute independence algorithms. The proposed approach considering the attribute independence achieved a high level of accuracy.

Figure 6: Recall versus precision for both attribute dependence and attribute independence.

Discussions

The main contribution of the second proposed method is that it considers dependencies among attributes. In the first proposed solution, the authors proposed a relational approach for identity uncertainty for citation matching using the Relational Probabilistic model that captures the dependence among multiple records but not among the attributes. The second paper used the dependencies among the attributes and modelled them as a Bayesian network.

As we mentioned before, identity uncertainty has been applied to many different fields. Like all data science tasks, the approach used for identity uncertainty depends on the data, available attributes, and generally to the application that the approach is applied to. The two papers that I discussed have been applied to different applications: one has been applied to citation matching and one to person identification. Therefore, the results in one paper may or may not apply to the other. As an example, the second paper showed that using the dependencies among attributes is quite helpful for the person identifying task, but this may not be the case for the citation matching in the first paper.

In the second paper, the social insurance number (SIN) is one of the attributes. One thing that may come to the reader's mind is that the accuracy that the authors gained is due to using SIN, which can be viewed as a primary key. But the accuracy is not the point that this paper is trying to make. This paper aims at showing how the attribute dependence model compares to attribute independence model, while using the same attributes (including SIN) and data for both models. The authors have shown that using the dependence attributes can be quite helpful.

The second paper uses synthesized data, but the first one uses real data. One may be more confident about a method whose accuracy has been tested on real data, as there is always the possibility of a bias in synthesized data. So I believe the first paper has stronger evaluations/results.

To Add

Put links and content here to be added. This does not need to be organized, and will not be graded as part of the page. If you find something that might be useful for a page, feel free to put it here.