Course:CPSC522/Differential Privacy

Introduction to Differential Privacy

Principal Author: Yilin Yang
Collaborators:

Abstract

As we rely more and more on technology, data safety issues nowadays have become more and more prevalent. In light of this unprecedented amount of data used to train models, how do we protect users/data from malicious actors who want to infer this information? An obvious choice will be to choose to omit sensitive features in the dataset, or only report averaged results, however as Dwork et al. has pointed out, these "protection" methods are too naive. Unsurprisingly, even simple attacks are very effective: For two datasets that record voter information and healthcare information while omitting the name, using natural joins is enough to connect two datasets and learn more about an individual, as addresses (or a combination of information) are unique to a very small set of people. Therefore, it's not difficult for adversarial users to obtain critical information. In fact, one of the most famous machine learning competitions, the Netflix recommendation system competition, was subject to privacy risks using the natural join as shown here. Such attacks are so simple in fact that even curious users can pull them off accidentally, and they facilitate the need for a gold standard privacy notion. In this page, we introduce the gold standard privacy notion of Differential Privacy (DP). DP is mathematically guaranteed to preserve privacy and is widely deployed in the industry by tech companies such as Apple, Google, and Facebook. It is even used in the 2020 US census to protect individual privacy. We will follow the notations by Dwork et al. who first introduced DP. We will begin with a formal definition of privacy and DP. We will then introduce a mechanism that can be used to achieve DP, we will then talk about DP properties and finally introduce approximate DP and its mechanisms. We will also beifly go over Rényi DP as a more recent development in DP.

Builds on

As DP is a mathematical guarantee, Probability is the main foundation. However, understanding Rényi Divergence is recommended for the last section.

Related Pages

The Algorithmic Foundations of Differential Privacy by Dwork et al. should be your go-to for most theory DP related.

Programming Differential Privacy is a much simpler overview that goes into implementation more than theory.

CS 860 - Algorithms for Private Data Analysis by Gautam Kamath has very good insight into the more dense proofs of DP, I highly recommend!

Hopefully, all of these along with this Wiki page can provide some well-needed insight into my previous page:

MDP for Differentially Private Reinforcement Learning

For those interested in the 2020 US Census, the blog post by Simson Garfinkel offers excellent insight.

Definition of Privacy and Differential Privacy

Before we introduce Differential Privacy, it is important to formally define privacy as it greatly changes our method of preserving privacy: if the goal is to not leak any information about the population, then every statistical/machine learning method that aims to preserve this notion of privacy cannot be of any use to analysts. However, if we define privacy as protection for members that participated in the training dataset so that there is no incurred risk for participating in the training process, then as ML researchers we can still obtain statistically significant knowledge of the population. We will use this definition of privacy, more formally:

Definition of Privacy:

Data Privacy aims to preserve the sensitive information of participants from malicious individuals while allowing data analysts to conduct statistically significant inferences of the data.

Definition of Differential Privacy

Following the definition by Dwork et al., for some Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \varepsilon \geq 0} , A mechanism Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{M}} is called Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \varepsilon} -DP if and only if it satisfies the equation:Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \Pr[\mathcal{M}(\mathcal{D})\in S] \le e^\epsilon\cdot \Pr[\mathcal{M}(\mathcal{D'})\in S] } for all neighboring datasets Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{D}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{D'}} and for all possible sets of the mechanism's output Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle S} .

Here, datasets are considered neighboring if they differ by only 1 entry, and a mechanism Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{M}} is any function that satisfies DP.

The DP definition essentially implies that the mechanism Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{M}} cannot be deterministic and must have multiple outputs given some input, and the output for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{M}(\mathcal{D})} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{M}(\mathcal{D'})} should be very similar to each other. This ensures that the adversary cannot infer whether or not a specific individual has partaken in the dataset, thereby protecting the user and its sensitive information. To make this clearer:

Example of the Differential Privacy Definition, here neighboring datasets have approximately the same output.

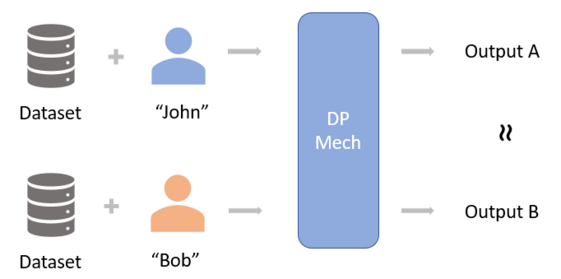
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \varepsilon} here is also known as the privacy budget or privacy parameter, the larger Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \varepsilon} is the less private Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{M}} becomes as there is more difference in the output for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{M}(\mathcal{D})} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{M}(\mathcal{D'})} . However it should be noted that the exact nature of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \varepsilon} is not fully understood, in other words, how do we choose Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \varepsilon} in practice? Even companies like Google, Apple, and Facebook who actively deploy DP models to preserve their users' privacy will typically choose an empirical value (or so they claim). In most cases, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \varepsilon} should be 1 or smaller, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \varepsilon} greater than 10 offers little to no privacy.

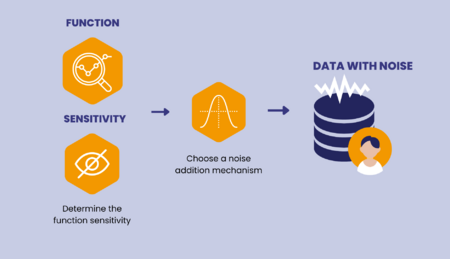
With the definition in hand, how does a function become a DP mechanism Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{M}} ? At a high level, DP can be achieved by injecting noise into a sensitive portion of the training procedure. This noise acts as a privacy barrier that obscures the 1-to-1 relationship of input and output, making any information past the privacy wall "sanitized". This barrier does not need setup such as in a database denying costly access restrictions like in databases as this added noise will make the results of such a query useless for malicious actors. Naturally, injecting noise will degrade the performance of an ML model, and researchers need to balance the tradeoff between protection and performance. In the next section, we will look at the Laplace Mechanism, a classic Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \varepsilon} -DP mechanism achieved by adding controlled Laplace noise.

Laplace Mechanism

Before we introduce the Laplace mechanism, we must define the sensitivity considered in the Laplace Mechanism:

Definition 1: Following the definition by , for any given function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle f(x) : \mathcal{D}^n \rightarrow \mathbb{R}^k} , the sensitivity of the function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle f} is:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \Delta_f = \max_{\mathcal{D}, \mathcal{D'}}||f(D)-f(D')||_1,} Where once again Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{D}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{D'}} are neighboring datasets.

This sensitivity is called the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle l_1} -sensitivity. There are multiple definitions of sensitivity, and they are used to scale the DP noise to the magnitude of change when 1 data point is changed in the dataset. Thus ensuring our DP noise is on the correct scale. Now, we can introduce the Laplace Mechanism:

Theorem 1: For a function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle f(x) : \mathcal{D}^n \rightarrow \mathbb{R}^k} , the mechanism Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{M}} satisfies Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \varepsilon} -DP:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal {M}(x) = f(x) + \text{Lap}(\frac{\Delta_f}{\varepsilon})} Where Lap is the laplace distribution with paramters 0 and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \frac{\Delta_f}{\varepsilon}} . For the proof of such mechanism Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{M}} satisfies Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \varepsilon} -DP, please see Theorem 4 of Gautam's Lecture notes.

The typical noise addition for functions to achieve DP. A larger sensitivity will require more DP noise.

Laplace Mechanism Application: Counting Queries

One of the most classic examples of using the Laplace Mechanism to privatize the counting query result. The counting query in a database are queries that ask the question: "How many data points in the dataset have property/feature A?" In this case, the system will go through each data point and generate an indicator value and sum it up with a function say Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle f} . As each data point can change this sum by at most 1, the sensitivity of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle f} should be 1. Thus an Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \varepsilon} -DP algorithmn for the counting queries is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle f(\mathcal{D}) + \text{Lap}(1/\varepsilon)} . The returned mechanism will have an error of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle O(1/\varepsilon)} and is independent of the dataset size.

There are many other use cases for the Laplace Mechanism, including privatizing histogram queries. In the next section, we will showcase the useful properties of DP.

Important Properties of Differential Privacy

DP is a popular choice of privatization not only because of its intuitive mechanisms, but also the convenient properties that follow from the DP definition. Here we will introduce the three most commonly used DP properties in research: post-processing, (basic) composition, and group privacy. We will include the proof as they are simple, but the proofs are largely inspired by Gautam's Lecture notes.

Post-Processing

Post-Processing is one of the most important qualities of DP, as it essentially guarantees any downstream task will not "un-DP" sensitive data that has been privatized.

Theorem 2: Let a mechanism Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{M} : \mathcal{D}^n \rightarrow \mathcal{Y}} be Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \varepsilon} -DP, and let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{F} : \mathcal{Y} \rightarrow \mathcal{Z}} be a randomized mapping algorthim, then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{F} \ \circ \ \mathcal{M}} is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \varepsilon} -DP.

Proof. As Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{F}} is randomized, it can be considered as some distribution of deterministic functions, say Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle f} . Thus for any neighbouring datasets Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{D}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{D'}} and output Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle S \subseteq \mathcal{Z}} :Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \begin{align} \Pr [ \mathcal{F}(\mathcal{M}(\mathcal{D}))\in S] &= \mathbb{E}_{f\sim\mathcal{F}}[\Pr [\mathcal{M}(\mathcal{D})\in f^{-1}(S)]] \\ & \le \mathbb{E}_{f\sim\mathcal{F}}[e^\varepsilon\cdot \Pr [\mathcal{M}(\mathcal{D'})\in f^{-1}(S)]] && (\text{DP defintion})\\ & = e^\varepsilon \cdot \Pr [ \mathcal{F}(\mathcal{M}(\mathcal{D'}))\in S]\\ & &&\Box \end{align}}

(Basic) Composition

Another important property of DP is composition, in the case where we run k DP algorithms on the same dataset, how do we aggregate/compose the privacy budget of these k mechanisms?

Theorem 3: Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathbf{\mathcal{M}} = [\mathcal{M}_1, \dots, \mathcal{M}_k]} be a scequence of k Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \varepsilon} -DP mechanisms, then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{M}} is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle k\varepsilon} -DP.

Proof. For any neighbouring datasets Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{D}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{D'}} and output sequence Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle S = [S_1, \dots, S_k]} :

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \begin{align} \frac{\Pr[\mathcal{M}(\mathcal{D}) = S]}{\Pr[\mathcal{M}(\mathcal{D'}) = S]} &= \prod^k_{i=1} \frac{\Pr[\mathcal{M}_i(\mathcal{D}) = S_i| [\mathcal{M}_1(\mathcal{D}), \dots , \mathcal{M}_{i-1}(\mathcal{D})] = [S_1, \dots, S_{i-1}]]}{\Pr[\mathcal{M}_i(\mathcal{D}) = S_i| [\mathcal{M}_1(\mathcal{D'}), \dots , \mathcal{M}_{i-1}(\mathcal{D'})] = [S_1, \dots, S_{i-1}]]}\\ &\le \prod^k_{i=1} e^\varepsilon\\ &= e^{k\varepsilon}\\ & &&\Box \end{align}} This is called basic composition because this budget bound is not the tightest, more recently there is the advanced composition which improves this bound to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle O(\sqrt{k})\varepsilon} -DP rather than the current Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle k\varepsilon} -DP. We will introduce the advanced composition later when we discuss approximate DP.

Group Privacy

Last but not least, we can extend the neighboring dataset definition to datasets that differ by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle k} entries, this is called group privacy. Similar to the DP definition:

Theorem 4: Let a mechanism Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{M} : \mathcal{D}^n \rightarrow \mathcal{Y}} be Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \varepsilon} -DP, thus for all datasets Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{D}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{D'}} that differ by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle k} data points, and for all possible sets of the mechanism's output Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle S} .Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \Pr[\mathcal{M}(\mathcal{D})\in S] \le e^{k\epsilon}\cdot \Pr[\mathcal{M}(\mathcal{D'})\in S] } Proof. Defining Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{D}_0 = \mathcal{D}} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{D}_k = \mathcal{D'}} , and the sequence from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{D}_0, \dots, \mathcal{D}_k} as a sequence of neighboring datasets, for all possible sets of the mechanism's output Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle S} , we have:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \begin{align} \Pr[\mathcal{M}(\mathcal{D}_0)\in S] &\le e^{\epsilon}\cdot \Pr[\mathcal{M}(\mathcal{D}_1)\in S] \\ &\le e^{2\epsilon}\cdot \Pr[\mathcal{M}(\mathcal{D}_2)\in S] \\ & \dots \\ &\le e^{k\epsilon}\cdot \Pr[\mathcal{M}(\mathcal{D}_k)\in S] \\ & &&\Box \end{align} } Thus we have learned the three most important properties that help DP to be an intuitive way of adding privacy protection, in practice however Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \varepsilon} -DP is a rather strong guarantee, in the next section, we will talk about the more widely used Approximate DP as it is known to give a better utility-privacy tradeoff.

Approximate Differential Privacy

Similar to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \varepsilon} -DP, we introduce a relaxation of this guarantee called approximate DP:

Definition 2: Following the definition by Dwork et al. , for some Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \varepsilon, \delta \geq 0} , A mechanism Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{M}} is called Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle (\varepsilon, \delta)} -DP if and only if it satisfies the equation:Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \Pr[\mathcal{M}(\mathcal{D})\in S] \le e^\epsilon\cdot \Pr[\mathcal{M}(\mathcal{D'})\in S] + \delta } for all neighboring datasets Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{D}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{D'}} and for all possible sets of the mechanism's output Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle S} .

Here, the only difference from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \varepsilon} -DP is the addition of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \delta} . Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \delta} is called the failure probability, we can summarize its behaviour into two cases:

• With a probability of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle 1 - \delta} , we have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \varepsilon} -DP: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \Pr[\mathcal{M}(\mathcal{D})\in S] \le e^\epsilon\cdot \Pr[\mathcal{M}(\mathcal{D'})\in S] } .
• With a probability of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \delta} , we get no privacy guarantee!

At first glance, this seems like a very scary definition, as there's a possibility that this algorithm will fail and leak sensitive data! Therefore in practice, this failure probability will be very small. Although it is still not enough to satisfy some DP purists (nothing ever does anyways), In the following sections we will see Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle (\varepsilon, \delta)} -DP mechanism that fail gracefully, and instead of releasing a sensitive dataset when it fails, instead they release the sensitive data with a weaker DP guarantee.

Gaussian Mechanism

Before we introduce the Gaussian mechanism, similar to the Laplace Mechanism we must define the sensitivity considered:

Definition 3: For a function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle f(x) : \mathcal{D}^n \rightarrow \mathbb{R}^k} , the sensitivity of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle f} is:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \Delta_f = \max_{\mathcal{D}, \mathcal{D'}}||f(D)-f(D')||_2,} Where once again Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{D}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{D'}} are neighboring datasets.

This sensitivity is called the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle l_2} -sensitivity. Now, we can introduce the Gaussian Mechanism:

Theorem 5: For a function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle f(x) : \mathcal{D}^n \rightarrow \mathbb{R}^k} , the mechanism Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{M}} satisfies Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle (\varepsilon, \delta)} -DP:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal {M}(x) = f(x) + \mathcal{N}(0, \sigma^2\Delta_f^2\mathbf{I}_p)} The (privacy) parameter Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \sigma} for a single privacy release satisfies the following inequality: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \sigma \geq \sqrt{2\log(1.25/\delta)}/\epsilon} hold for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \epsilon \leq 1} .

For the proof of such mechanism Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{M}} satisfies Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle (\varepsilon, \delta)} -DP, please see Theorem 6 of Gautam's Lecture notes. In the following section we will outline the properties that Approximate DP has.

Important Properties of Approximate Differential Privacy

Similar to the properties in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \varepsilon} -DP, Approximate DP also offers such useful properties. Here, as some proofs are dense we will only state the results, those who are interested in the details can refer to the works by Dwork et al. and Vadhan .

Post-Processing

The post-processing property still holds, and the proof is pretty straightforward as you replace the DP definition with the approximate DP definition:

Theorem 6: Let a mechanism Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{M} : \mathcal{D}^n \rightarrow \mathcal{Y}} be Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \varepsilon} -DP, and let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{F} : \mathcal{Y} \rightarrow \mathcal{Z}} be a randomized mapping algorthimn, then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{F} \ \circ \ \mathcal{M}} is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle (\varepsilon, \delta)} -DP.

Basic Composition

Theorem 7: Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathbf{\mathcal{M}} = [\mathcal{M}_1, \dots, \mathcal{M}_k]} be a sequence of k Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle (\varepsilon, \delta)} -DP mechanisms, where each Mechanism Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{M}_i} is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle (\varepsilon_i, \delta_i)} -DP then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{M}} is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle (\sum^k_{i=1}\varepsilon_i, \sum^k_{i=1}\delta_i)} -DP.

Advanced Composition

As stated previously, if we used Advanced Composition, we can improve the aggregated/composed privacy budget of DP algorithms.

Theorem 8: Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathbf{\mathcal{M}} = [\mathcal{M}_1, \dots, \mathcal{M}_k]} be a sequence of k Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle (\varepsilon, \delta)} -DP mechanisms, where each Mechanism Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{M}_i} has the same privacy parameters Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \varepsilon_i = \varepsilon} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \delta_i = \delta} . then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{M}} 's is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle (\varepsilon\sqrt{8k\ln(1/\delta')}, k\delta + \delta')} -DP.

Here Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \delta' > 0} , and it's a value that can be manually changed and provides a relationship between the composed Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \tilde{\varepsilon} = \varepsilon\sqrt{8k\ln(1/\delta')}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \tilde{\delta} = k\delta + \delta'} . The exact proof of this bound is detailed in the paper by Dwork et al. But the intuition can be found in Gautam's DP Lecture 6 . Notice that Approximate DP is equivalent to DP when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \delta = 0} , this bound holds for both DP definitions. This which improves the privacy parameter Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \tilde\varepsilon} to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle O(\sqrt{k})\varepsilon} rather than the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle k\varepsilon} in basic composition.

Group Privacy

Last but not least, we also have group privacy in Approximate DP:

Theorem 9: Let a mechanism Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{M} : \mathcal{D}^n \rightarrow \mathcal{Y}} be Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle (\varepsilon, \delta)} -DP, thus for all datasets Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{D}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{D'}} that differ by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle k} data points, and for all possible sets of the mechanism's output Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle S} .Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \Pr[\mathcal{M}(\mathcal{D})\in S] \le e^{k\epsilon}\cdot \Pr[\mathcal{M}(\mathcal{D'})\in S] + ke^{(k-1)\varepsilon}\delta } Here, the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \delta} has an additional factor of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle e^{(k-1)\varepsilon}} .

Failure Probability Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \delta} in the Gaussian Mechanism

We mentioned in the previous section how the Gaussian Mechanism is not Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \varepsilon} -DP, instead with failure probability Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \delta} , it is a graceful failure with a weaker DP guarantee.

In other words, with probability Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \delta} , the Gaussian Mechanism satisfies Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle t\varepsilon} -DP instead, for some value Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle t} .

As for what this value Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle t} is, the proof Theorm 6 of Gautam's Lecture notes provides a more detailed explaination.

Finally, we have talked about the most common properties in DP and approximate DP, and why it is widely recognized in both academics and industry as the gold standard privacy notion. In the next section, we will look at a more up-to-date Approximate DP method, Rényi Differential Privacy.

Rényi Differential Privacy

In statistics, there are many divergence metrics used to compare probability distributions. As the DP definition is essentially a probability distribution comparison, researchers have thought of applying these metrics to the DP definition in hopes of improving the bounds of the DP properties stated previously. These metrics, such as the max divergence, KL divergence, and Rényi divergence have sparked variants of DP as they can be directly transformed back to the original DP definition. Here, we will look at the most widely used Rényi Differential Privacy (RDP), we will begin by introducing the definition of the Rényi Divergence:

Definition 4: For two probability distributions Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{P}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{Q}} , the Rényi Divergence is defined as:Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle D_\alpha(\mathcal{P}\ ||\ \mathcal{Q}) = \frac{1}{\alpha - 1}\log\big(\sum^n_{i=1}\mathcal{p}_i ^\alpha q^{1-\alpha}_i\big) } When Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \alpha \rightarrow 1 } , this is the KL-divergence and when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \alpha \rightarrow \infty } we can recover the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \varepsilon} -DP definition (This is just pure mathematics). We can use Rényi Divergence at various other Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \alpha } to have a better relaxation of DP while avoiding the failure probability in Approximate DP. We now formally introduce RDP which is first proposed by Mironov :

Definition 5: A mechanism Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{M}} is called Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle (\alpha, \bar{\epsilon})} -RDP if and only if it satisfies the equation:Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle D_\alpha(\mathcal{M}(\mathcal{D})\ ||\ \mathcal{M}(\mathcal{D'})) \le \bar{\epsilon} } for all neighboring datasets Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{D}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{D'}} . Here Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \bar{\epsilon} } should be differentiated from the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \varepsilon} in the DP definitions.

The relationship between Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle (\alpha, \bar{\epsilon})} -RDP and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle (\varepsilon, \delta)} -DP are as follows:

Theorem 10: Let a mechanism Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{M} : \mathcal{D}^n \rightarrow \mathcal{Y}} be Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle (\alpha, \bar{\epsilon})} -RDP, then for some Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \delta > 0} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{M}} is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle (\varepsilon, \delta)} -DP where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \varepsilon = \bar{\epsilon} + \frac{\log(1/\delta)}{\alpha -1}} .

Here, the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \delta} can once again be manually changed by the data scientists but a small value might be more sensible. One of the most mechanism that achieves Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle (\alpha, \bar{\epsilon})} -RDP is, once again, the Gaussian Mechanism:

Theorem 11: For a function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle f(x) : \mathcal{D}^n \rightarrow \mathbb{R}^k} , the mechanism Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{M}} satisfies Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle (\varepsilon, \delta)} -DP:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal {M}(x) = f(x) + \mathcal{N}(0, \frac{\Delta_f^2\alpha}{2\bar\epsilon})} One of the biggest advantage in using this RDP Gaussian Mechanism is that the composition can be tight, without the need for advanced composition:

RDP Composition

Theorem 12: Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathbf{\mathcal{M}} = [\mathcal{M}_1, \dots, \mathcal{M}_k]} be a sequence of k Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle (\alpha, \bar{\epsilon})} -RDP mechanisms, where each Mechanism Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{M}_i} is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle (\alpha, \bar{\epsilon}_i)} -RDP then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle \mathcal{M}} is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle (\alpha, \sum^k_{i=1}\bar{\epsilon}_i)} -RDP.

This bound is particularly powerful as even transforming it back to the original definition of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wiki.ubc.ca/api/rest_v1/":): {\displaystyle (\varepsilon, \delta)} -DP we get a much better privacy cost than advanced composition. Consequently, RDP has been used in Goggle's TensorFlow Privacy package for privacy accounting.

Conclusion

In this Wiki page, we provide a comprehensive overview and introduction to DP, a gold standard notion of privacy. We carefully defined privacy and showcased how DP is a powerful mathematical guarantee of this notion of privacy. There are many DP variants and mechanisms not introduced as it is far beyond the scope of this course, however, I highly recommend checking out Zero-Concentrated Differential Privacy by Bun and Steinke as well as many DP papers in machine learning conferences as there are active researchers from all over the world who are in active pursuit of closing the gap between DP and non-DP settings. Ultimately, if DP doesn't degrade the performance, it can be trivial to deploy and privacy in ML will be achieved.

Annotated Bibliography

Put your annotated bibliography here. Add links where appropriate.