Course:CPSC312-2018-Ray-tracer
Ray-tracer

Authors:
Jerry Yin, James Johnson
What is the problem?
For the project, we will implement a ray-tracer in Haskell based on Prof. Peter Shirley's notes. Our ray-tracer will feature
- sphere scene objects,
- three materials: a diffuse, refractive, and reflective material,
- anti-aliasing,
- brute-forced global illumination (light rays recursively bounce around the scene),
- depth of field (defocus blur), and
- PNG output (provided by third-party library).
Our ray-tracer in particular is a path tracer. Path tracing is essentially a Monte Carlo method for realistically drawing 3D objects by randomly bouncing light rays throughout the scene, and averaging the results of each of these samples. The image quality increases with the number of samples.
-
Image rendered with 2 samples per pixel (spp).
-
Image rendered with 256 spp.
What is the something extra?
Since ray-tracing is known to be an "embarrassingly parallel" problem, our ray-tracer supports ray-tracing on multiple cores. To support this, we investigated Haskell's parallelism libraries and performed benchmarking. Benchmarks are in the next section.
Even though we used a third-party library, Repa, to deal with the low-level work of spawning and managing threads, we still needed to deliberately write our code in a way that was parallelizable. For example, we had to create multiple uncorrelated random number generators in order to get sampling to work. See the next section for details.
What did we learn from doing this?
Random Number Generation
In a sequential Haskell program, random numbers can be generated by threading an infinite sequence of random numbers throughout the flow of the program. Random numbers can be taken from the head of the list, and the tail is returned to the caller.
However, in a parallel program like ours, we need at least one arbitrarily long random sequence per thread, since each thread needs to be able to generate random numbers independently of all other threads. We then run into a problem: what value do we use to seed each random number generator? (Time doesn't work if the threads are spawned at roughly the same time.)
For simplicity, we created one infinite random list for each sample. Initially our code incremented the seed value by one for each sample. This resulted in visible banding artifacts.
-
Image rendered using "increment by one" scheme of seeding. Note the banding artifacts, especially in the shadows.
-
Image rendered using better random number generation. Note that the banding artifacts have been replaced with a layer of high-frequency noise. This is caused by the variance in the Monte Carlo simulation.
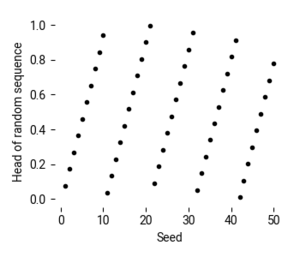
Further investigation into the System.Random random number generator revealed that random sequences from close together seeds are highly correlated.
Prelude> import System.Random Prelude System.Random> [head (randoms (mkStdGen x)) :: Double | x <- [1..10]] [7.779037508334341e-2,0.17372420460863047,0.2696580341339174, 0.3655506172458505,0.46148444677113754,0.5574180378778549,0.6533518674031419, 0.7492446889336446,0.845178280040362,0.9411121095656491]
Above, you can see that the head of the sequence essentially increases by 0.1 for each increase in the seed.
The above graph suggests that bands might be created by sudden discontinuities in the graph above. Even more subtly, by using correlated random samples we introduce statistical bias into the Monte Carlo simulation.
One solution to this problem is to generate the seeds from a random number generator at the root process, and then pass the resulting infinite lists to the child processes before any ray-tracing is done. Here is how we did it in an earlier version of our code:
-- | Generate an array of RNGs (one for each AA sample).
rngs :: Array Int RNG
rngs = listArray (0, count)
(take count [mkRNG seed | seed <- randoms (mkStdGen 0)])
where count = ny * nx * ns + nx * ns + ns - 1
-- | Get the RNG for a given sample.
getRNG :: Int -> Int -> Int -> RNG
getRNG x y s = rngs Data.Array.! (y * nx * ns + x * ns + s)
Thus, sample s of pixel (x, y) can retrieve its RNG sequence in constant time by calling getRNG x y s. This approach fixes the banding problems but creates a substantial sequential bottleneck before the parallel code can begin running.
Our final approach was to decorrelate the seeds using a high-frequency sine function (which can double as a deterministic random function in a pinch).
-- | Given a range of integer inputs, return integer outputs that appear to be
-- uncorrelated to the supplied inputs. We use this function to generate
-- "random" seeds.
decorrelate :: Int -> Int
decorrelate x =
-- very high-frequency sine works well here for producing "random-ness"
floor (maxInt * (sin (fromIntegral (2000000000 * x) :: Double)))
where maxInt = fromIntegral (maxBound :: Int)
Thus, each sample can generate both its seed of decorrelate (y*nx*ns + x*ns + s) and its corresponding random sequence independently of all other samples.
Benchmarks
Parallel performance is paramount in ray-tracing. Because ray-tracing is "embarrassingly parallel", good speedups can make up for somewhat poorer sequential run-time in comparison to ray-tracers implemented in more low-level languages.
Here are the results I got from running on a 3 GHz Intel i7-4500U with 4 cores (and 8 hyperthreaded cores) on Ubuntu 18.04, ghc 8.6.1:
$ time cabal new-run ray-tracer -- -s 32
Up to date
Options {samples = 32, maxBounces = 8, output = "out.png", gamma = 2.2}
cabal new-run ray-tracer -- -s 32 9.70s user 0.04s system 99% cpu 9.753 total
$ time cabal new-run ray-tracer -- -s 32 +RTS -N2
Up to date
Options {samples = 32, maxBounces = 8, output = "out.png", gamma = 2.2}
cabal new-run ray-tracer -- -s 32 +RTS -N2 10.18s user 0.20s system 197% cpu 5.253 total
$ time cabal new-run ray-tracer -- -s 32 +RTS -N4
Up to date
Options {samples = 32, maxBounces = 8, output = "out.png", gamma = 2.2}
cabal new-run ray-tracer -- -s 32 +RTS -N4 19.43s user 0.44s system 384% cpu 5.163 total
The first run represents a fully sequential run on one core, whereas the second and third runs represent rendering with 2 and 4 cores respectively. We see that the speedup for the 2-core case is actually quite reasonable! Since we have no non-trivial data dependencies, we expect an ideal speedup of 2 on 2 cores, and we got a speedup of 9.753 / 5.253 = 1.86 in practice. However, by rendering on 4 cores, we don't improve over the 2-core case by much, despite having good utilization (384%).
However, the ease at which we could add parallelism to our code should not be understated. By using Repa and Haskell's lack of side effects, we can simply write a ordinary "sequential" function to perform sampling, and pass this function off to Repa to evaluate in parallel.
Functional
One nice affordance functional programming offered us was that instead of single method interfaces for primitives and materials, we could define these types as functions to pass around instead:
-- | Calculate if ray hits primitive between tmin and tmax return 'Nothing' on a -- miss type Primitive = Ray -> Double -> Double -> Maybe HitRecord -- | Takes an incoming ray and and its associated 'HitRecord', and returns the -- attenuated color and an outgoing scatter ray, or 'Nothing' for a miss. type Material = Ray -> HitRecord -> RNG -> (Maybe (Vec3, Ray), RNG)
However, the need to thread RNGs throughout our program results in some significant boilerplate code, and also creates opportunities for mistakes (what if we pass a sequence other than the tail?).
Conclusion
In summary, writing a ray-tracer in Haskell ended up being quite straightforward, despite than our battles with Haskell's poor random number generation facilities. Haskell allowed us to parallelize elegantly-written code without worrying about mutual exclusion, locks, etc. due to its lack of side effects, and we achieved decent speedups on 2 cores.
Links to code
https://github.com/enjmiah/ray-tracer
Attributions
See https://github.com/enjmiah/ray-tracer/blob/master/NOTICES.