Course:ASTR508/Additional Notes

Equation of State

Reading Assignment

Chapter 5 of Stellar-Astrophysics Notes

Radiative Transfer

Reading Assignment

Chapter 6 of Stellar-Astrophysics Notes

Introduction

We are going to set the stage for a deeper look at astrophysical sources of radiation by defining the important concepts of radiative transfer, thermal radiation and radiative diffusion.

One can make a large amount of progress by realizing that the distances that radiation typically travels between emission and detection or scattering etc. are much longer than the wavelength of the radiation. In this regime we can assume that light travels in straight lines (called rays). Upon these assumptions the field of radiative transfer is built.

Flux

Let's start with something familiar and give it a precise definition. The flux is simply the rate that energy passes through an infinitesimal area (imagine a small window).

$dE=FdAdt$

For example, if you have an isotropic source, the flux is constant across a spherical surface centered on the source, so you find that

$E_{1}=F_{1}4\pi R_{1}^{2}~{\rm {and}}~E_{2}=F_{2}4\pi R_{2}^{2}$

at two radii around the source. Unless there is aborption or scattering between the two radii, $E_{1}=E_{2}$ and we obtain the inverse-square law for flux

$F_{1}R_{1}^{2}=F_{2}R_{2}^{2}.$

Intensity

Although the flux is a useful quantity, it cannot encapsulate all of our knowledge about a radiation field. For example, one could shine a faint light directly through a window or a bright light through the same surface at an angle. Both of these siutations are characterized by the same rate of energy flow through the surface, but they are clearly different physical situations.

A more generally useful quantity quantifies the rate that energy flows through a surface in a particular direction (imagine that the window now looks into a long pipe so that only photons travelling in a particular direction can pass through.

$dE=IdAd\Omega dt$

Although this quantity seems a bit kludgy, it is actually quite familiar. It is the brightness.

You look at a light bulb. As you move away from the light bulb, your eye recieves less flux ($F$ decreases) and the apparent size of the light bulb also decreases ($d\Omega$ decreases). It turns out that these two quantities both decrease as $R^{-2}$, so the intensity or brightness is conserved along a ray. This result makes the intensity a terrifically useful quantity.

Relation to the flux

From the example at the beginning of this section we can deduce the relationship between the flux and the intensity of the light. Radiation that travels perpendicular to a surface delivers more energy to that surface than radiation travelling at an angle. You can always imagine second surface perpendicular to the light ray through which all of the energy that reaches the first surface travels. We know that intensity is the same along the ray so

$dE=IdA_{1}d\Omega dt=IdA_{2}d\Omega dt$

and $dA_{2}=\cos \theta dA_{1}$, so the total flux travelling through the surface is given by a moment of the intensity

$F=\int I\cos \theta d\Omega$

If $I$ is constant with respect to angle, there is as much energy travelling from left to right as from right to left, so the net flux vanishes, or more mathematically the mean of $\cos \theta$ vanishes over the sphere.

Something to think about

The sun is equally intense in the summer and winter (if you exclude the effects of the atmosphere), then why are winters colder than summers?

A closely related quantity is the pressure that a radiation field exerts on a surface. Pressure is the rate that momemtum is delivered to a surface in the direction perpendicular to the surface. The momentum of an individual photon is $E/c$ and the rate that energy is delivered to a surface from photons travelling around a particular direction is simply $I\cos \theta d\Omega$. The component of the momentum that is directed perpendicular to the surface is $E\cos \theta /c$, so there is a second factor of $\cos \theta$ yielding the following integral.

$p={\frac {1}{c}}\int I\cos ^{2}\theta d\Omega .$

Something to think about

Does the radiation pressure from an isotropic radiation field vanish?

Spectra

The quantities that we have defined so far can be examined as a function of the frequency or wavelength of the radiation or the energy of the individual photons, yielding $F_{\nu },F_{E},F_{\lambda }$ and also for the intensity, e.g

$dE=F_{\nu }d\nu dAdt.$

The use of $F_{\nu }$ is so common that astronomers have a special unit to measure $F_{\nu }$

$1~{\rm {Jansky}}=1~{\rm {Jy}}=10^{-26}{Wm}^{-2}{Hz}^{-1}=10^{-23}{\rm {ergcm}}^{-1}{s}^{-1}{Hz}^{-1}.$

This unit is most commonly used in the radio and infrared, and sometimes in the x-rays.

A common combination that people use is

$EF_{E}=\lambda F_{\lambda }=\nu F_{\nu }=\nu {\frac {dF}{d\nu }}={\frac {dF}{d\ln \nu }}.$

This allows you to convert between $F_{\nu }$ and $F_{\lambda }$ etc. And it also gives the flux per logarithmic interval in photon energy or frequency. This is really handy since astronomers like to use log-log plots. A spectrum that goes as $F_{\nu }\propto 1/\nu$ has a constant amount of energy per logarithmic interval.

Something to think about

A source emits at 1 Jansky from 100~MHz to 1~GHz and at 1 $\mu$Jy from 1 to 10 keV. Is it brighter in the radio or x-rays?

An Astronomical Aside: Magnitudes

Astronomers typically speak about the flux of an object in terms of magnitudes. A magnitude is generally defined as

$m=-2.5\log _{10}\int _{0}^{\infty }g(\nu )F_{\nu ,\Omega }d\nu +m_{0}.$

What are the different quantities in this expression? Pogson empirically determined the value of '2.5' by comparing the magnitudes of prominent observers of the 1800's. It is remarkably close to $\ln 10\approx 2.3$, so a change in magnitude of 0.1 is about a ten-percent change in flux.

Another term in the expression is $g(\nu )$, the filter function that determines which part of the electromagnetic spectrum you're are looking at. If $g(\nu )=1$, the quantity is called a ``bolometric magnitude. It is supposed to quantify the total energy coming from the source. One also hears about a quantity called the 'bolometric correction' which is simply the difference between the magnitude of source for a particular filter ($g(\nu )$) and for $g(\nu )=1$.

$F(\nu ,\Omega )$ is the flux coming from the source as a function of frequency integrated over a certain area of sky, $\Omega$. For a star one generally can extrapolate the flux that one observes in the sky to the total flux, but the intensity from a galaxy or other extended source generally falls off gradually so one defines a magnitude within a certain aperture or down to a limiting intensity (surface brightness).

The final term is $m_{0}$, the zero point. The value of the zero point is a matter of convention. Two of the standard conventions are the 'Vega' convention which states that the magnitude of the star Vega regardless of the function $g(\nu )$ is zero; all of Vega's colours are zero. This works nicely because you could always in principle observe Vega with your equipment.

There are two problems however. One is that the flux from Vega like that of most stars varies as bit. The second is that an object with a flat spectrum (equal energies in each frequency interval) will have an awkward set of colours (the difference in magnitudes for two different $g(\nu )$ functions). This leads to the second convention, the AB system.

$m(AB)=-2.5\log _{10}f_{\nu }-48.60=-2.5\log _{10}\left({\frac {f_{\nu }}{1{\rm {Jy}}}}\right)+8.90$

where $f_{\nu }$ is the flux in c.g.s. units. The constants '8.90' and '-48.60' mean that $m(AB)=V$ for a flat spectrum source.

Something to think about

How do you define an AB magnitude using a filter?

A final quantity that astronomers talk about is the surface brightness. This is just the intensity that we have been speaking about all along. However, the conventional nomenclature is rather strange, magnitudes per square arcsecond.

Something to think about

What is the magnitude of a source that subtends 10 square arcseconds with a surface brightness of 19 magnitudes per square arcsecond?

Energy Density

Let's imagine that light is travelling through a small box. How much energy is in the box at any time? First it is easiest to think about how much energy in the box is travelling in a particular direction through the box during a small time interval such that $cdt$ is the length of the box,

$dE=u(\Omega )dAcdtd\Omega$

This energy equals the energy that enters the box travelling in the right direction during the time interval $dt$,

$dE=IdAdtd\Omega$

so

$cu(\Omega )=I.$

To get the total energy density you have to integrate over all of the ray directions

$u={\frac {1}{c}}\int Id\omega =4\pi {\frac {J}{c}}$

where $J$ is the mean intensity. Notice how it differs from the flux defined earlier.

Let's revisit the radiation pressure formula. But let's assume that the radiation field is isotropic, so $I=J$ for all directions, we get

${\begin{matrix}p&=&{\frac {1}{c}}\int J\cos ^{2}\theta d\Omega \\&=&{\frac {1}{c}}\int _{0}^{\pi }\int _{0}^{2\pi }J\cos ^{2}\theta \sin \theta d\theta d\phi \\&=&{\frac {1}{c}}J\left(2\pi \left.{\frac {1}{3}}\cos ^{3}\theta \right|_{0}^{\pi }\right)={\frac {4}{3}}\pi {J}{c}={\frac {1}{3}}u.\end{matrix}}$

A Physical Aside: What are the Intensity and Flux?

How do the intensity and flux fit in with more familiar concepts like the flux of a vector field? They really don't.

One can define the flux in three perpendicular directions by asking how much energy flows through three mutually perpendicular planes. This flux vector transforms like a vector under rotations, but it doesn't transform like a four-vector under boosts. The flux vector fills in the time-space components of the stress-energy tensor of the photon field. We have also calculated the time-time component which is the energy density and the space-space components, the pressure. To calculate how the flux transforms with respect to a boost (or Lorentz transformation) by transforming the entire tensor.

The intensity ($I_{\nu }$) as we shall soon see is simply related to the phase-space density of the ensemble of photons.

Blackbody Radiation

Blackbody radiation is a radiation field that is in thermal equilibrium with itself. In general we will find it convenient to think about radiation that is in equilibrium with some material or its enclosure. Using detailed balance between two enclosures in equilibrium with each other and the enclosed radiation we can quickly derive several important properties of blackbody radiation.

• The intensity ($I_{\nu }$) of blackbody radiation does not depend on the

shape, size or contents of the enclosure.

• Blackbody radiation is isotropic.

What remains is the temperature and the frequency. Because the intensity is a universal function of $T$ and $\nu$, we define

$B_{\nu }(T)\equiv I_{\nu }{\rm {~for~a~blackbody~at~temperature~}}T.$

Because heat flows from a hotter system to a cooler system we know that if $T_{1}>T_{2}$, $B_{\nu }(T_{1})>B_{\nu }(T_{2})$ for all values of $\nu$.

Thermodynamics

The blackbody radiation in its enclosure is a system in equilibrium so we can use the equations of thermodynamics to glean some more of its properties. If we deliver some heat $dQ$ to the blackbody, it can change the internal energy of the blackbody $dU$ or do work $p dV$. The heat delivered also equals the change in entropy of the system times the temperature of the system.

$dQ=TdS=dU+pdV.$

Now $U$ is simply the energy density times the volume of the enclosure so $dU=udV+Vdu/dTdT$ and we showed the $p=u/3$. Let's put this together

$TdS=udV+V{\frac {du}{dT}}dT+{\frac {1}{3}}udV.$

If we rearrange and solve for the derivatives we get

$\left({\frac {\partial S}{\partial T}}\right)_{V}={\frac {V}{T}}{\frac {du}{dT}}~~~~~~\left({\frac {\partial S}{\partial V}}\right)_{T}={\frac {4}{3}}{\frac {u}{T}}$

Let's take the partial derivative of the first expression with respect to $V$ and the second expression with respect to $T$ and set them equal

${\frac {1}{T}}{\frac {du}{dT}}={\frac {4}{3}}{\frac {1}{T}}{\frac {du}{dT}}-{\frac {4}{3}}{\frac {u}{T^{2}}}$

Let's solve for $du/dT$ to get

${\frac {du}{dT}}={\frac {4u}{T}}$

so $u=aT^{4}$ where $a$ is a constant of integration. This is the Stefan-Boltzmann law. The value of $a$ is $7.56\times 10^{15}$~erg~cm$^{-3}$K$^{4}$.

Something to think about

Why does $du/dV$ vanish?

We found that for an isotropic radiation field the energy density is simply related to the intensity, $u=4\pi J/c$. For a blackbody $J=B(T)$ so we have

$B(T)={\frac {ac}{4\pi }}T^{4}.$

Let's imagine that our blackbody enclosure has a small hole of area $dA$ in it. How much energy emerges through this hole

$FdA=\int _{\rm {out}}\cos \theta B(T)d\Omega =B(T)\int _{0}^{\pi }\int _{0}^{2\pi }\cos \theta \sin \theta d\theta d\phi =\pi B(T).$

We write this more compactly by defining $\sigma =ac/4$ so we have $F=\sigma T^{4}$ where $\sigma = 5.67 \times 10^{-5}$~erg~cm$^{-2}$s$^{-1}$K$^{-4}$.

Using the earlier results we can also derive the entropy of the radiation field

$S={\frac {4}{3}}aT^{3}V$

Statistical Mechanics

We have managed to derive several interesting properties of blackbody radiation but we still have no idea what its spectrum is. To figure this out we have to think about the microscopic properties of the radiation field. Let's imagine that we have blackbody radiation in a box whose wavenumber $k_{x}$ ranges from $k_{x}$ to $k_{x}+dk$. How many different types of waves lie in this interval?

You may be tempted to say as many as you want, but the waves are trapped in a box. Let's say that the box has length $l_{x}$ in the $x$-direction; therefore, $k_{x}l_{x}=2\pi n_{x}$ where $n_{x}$ is an integer so that the radiation field has a node at the edges of the box, so between $k_{x}$ and $k_{x}+dk$ there are only $2dkl_{x}/(2\pi )$ different states. The factor of two arises because the waves have two independent polarization states. If we imagine a small cube in phase space of size $dk_{x}dk_{y}dk_{z}$ we get

$dN=2{\frac {l_{x}l_{y}l_{z}}{(2\pi )^{3}}}d^{3}k=2{\frac {dV}{(2\pi )^{3}}}d^{3}k.$

Now we have $d^{3}k=k^{2}dkd\Omega$ and $k=2\pi \nu /c$ so

$d^{3}k=d\nu d\Omega {\frac {(2\pi )^{3}}{c^{3}}}\nu ^{2}$

We find that the density of states is given by

$\rho _{s}\equiv {\frac {dN}{dVd\Omega d\nu }}={\frac {2\nu ^{2}}{c^{3}}}$

The energy density ($u_{\nu }(\Omega )$)of the radiation field is simply the density of states times the mean energy per state and $cu_{\nu }(\Omega )=I_{\nu }$.

Classically we find that the mean energy per state is simply given by $kT$. Let's try this out for size,

$u_{\nu }^{\rm {classical}}(\Omega )={\frac {2\nu ^{2}}{c^{3}}}kT.$

This is the great Rayleigh-Jeans law and it actually works pretty well, unless you look at large frequencies and find that the total energy $B(T)$ is infinite. This is called the Rayleigh-Jeans (or ultraviolet) catastrophe.

The solution to this problem ushered in the era of modern physics. Planck argued that if light comes in discrete packages (photons) whose energy is proportional to the frequency we can solve this problem ($E=h\nu$). Let's try a really simple minded approach to assume that only photons with $E<kT$ are in the radiation field then we have

$u_{\nu }^{\rm {classicalfixed?}}(\Omega )=\left\{{\begin{array}{ll}{\frac {2\nu ^{2}}{c^{3}}}kT&h\nu <kT\\0&h\nu \geq kT\end{array}}\right.$

Let's integrate $u_{\nu }$ over the frequency range and solid angle to get

$u^{\rm {classicalfixed?}}={\frac {8\pi kT}{3c^{3}}}\left({\frac {kT}{h}}\right)^{3}={\frac {8\pi k^{4}}{3c^{3}h^{3}}}T^{4}.$

This has the right behaviour and the numerical constant differs from the actual value by a factor of about 20.

It turns out that we can do a whole lot better. According to statistical mechanics the probability of a state of energy $E$ is proportional to $e^{-\beta E}$ where $\beta =1/(kT)$. The energy in a particular state is proportional to the number of photons in the state $E_{n}=nh\nu$. The mean energy in a state is given by

${\bar {E}}={\frac {\sum _{n=0}^{\infty }E_{n}e^{-\beta E_{n}}}{\sum _{n=0}^{\infty }e^{-\beta E_{n}}}}$

Notice that the expression on the top is the derivative of the expression on the bottom with respect to $\beta$, so we find

${\bar {E}}=-{\frac {\partial }{\partial \beta }}\left(\sum _{n=0}^{\infty }e^{-\beta E_{n}}\right).$

We haven't assume anything about the states themselves yet, so this result would apply for any system. Here we know that $E_{n}=nh\nu$ so

$\sum _{n=0}^{\infty }e^{-\beta E_{n}}=\sum _{n=0}^{\infty }r^{n}={\frac {1}{1-r}}={\frac {1}{1-e^{-\beta h\nu }}}$

so

${\bar {E}}={\frac {h\nu }{e^{\beta h\nu }-1}}$

For $h\nu \ll \ kT$ $\beta h\nu \ll \ 1$ so we have

${\bar {E}}\approx {\frac {h\nu }{1+\beta h\nu -1}}={\frac {h\nu }{\beta h\nu }}=kT,$

the classical result. But for $h\nu \gg \ kT$ we have $\beta h\nu \gg \ 1$

${\bar {E}}\approx h\nu \exp(-\beta h\nu ).$

If we use this value with the density of states we get the Wien law.

Let's derive the expression for the spectrum for all frequencies. We have the value of energy density

$u_{\nu }(\Omega )={\frac {2h}{c^{3}}}{\frac {\nu ^{3}}{\exp(h\nu /kT)-1}}$

so that

$B_{\nu }(T)={\frac {2h}{c^{2}}}{\frac {\nu ^{3}}{\exp(h\nu /kT)-1}}.$

This is the Planck law!!!

Something to think about

At what energy does the flux per logarithmic energy interval reach its peak?

Let's try to find the value of $a$.

$u_{\nu }=4\pi u_{\nu }(\Omega )={\frac {8\pi h}{c^{3}}}{\frac {\nu ^{3}}{\exp(h\nu /kT)-1}}$

The total energy density is $\int u_{\nu }d\nu$

$u=\int _{0}^{\infty }{\frac {8\pi h}{c^{3}}}{\frac {\nu ^{3}}{\exp(h\nu /kT)-1}}d\nu ={\frac {8\pi h}{c^{3}}}\left({\frac {kT}{h}}\right)^{4}\int _{0}^{\infty }{\frac {x^{3}}{e^{x}-1}}dx.$

The integral can be evaluated using a Taylor series

$\int _{0}^{\infty }{\frac {x^{3}}{e^{x}-1}}dx=\int _{0}^{\infty }{\frac {x^{3}e^{-x}}{1-e^{-x}}}dx=\int _{0}^{\infty }x^{3}\sum _{n=1}^{\infty }e^{-nx}dx=\sum _{n=1}^{\infty }{\frac {6}{n^{4}}}$

to yield $\pi ^{4}/15$.

Blackbody Temperatures

A blackbody is of course characterized by a single temperature, $T$. However, it is often convenient to characterize the radiation from astrophysical sources by assuming that it is a blackbody and using some property of the blackbody spectrum to derive a characteristic temperature for the radiation. There are three characteristic temperatures in common usage: brightness temperature, effective temperature and the colour temperature.

The brightness temperature is determined by equating the brightness or intensity of an astrophysical source to the intensity of a blackbody and solving for the temperature of the corresponding blackbody.

$I_{\nu }=B_{\nu }(T_{b}).$

This expression is most useful in the regime where the intensity of the blackbody is proportional to the temperature i.e. the Rayleigh-Jeans limit. Here we have,

$T_{b}={\frac {c^{2}}{2\nu ^{2}k}}I_{\nu }.$

The brightness temperature has several nice properties. For one thing it has units of Kelvin rather than something clumsy. Second if a material is emitting thermal radiation one can obtain a simple expression of the radiative transfer equation (see the problems).

Something to think about

In what regime does the linear relationship between the brightness temperature and the intensity begin to fail? How can you tell?

The colour temperature is defined by looking at the peak of the emission from the source and using Wein's displacement law to define a corresponding temperature. This may be done in a more sophisicated manner by fitting a blackbody spectrum or something like that.

Finally the effective temperature is the temperature of a blackbody that emits the same flux per unit area as the source.

Radiative Transfer

As a ray passes through some material its intensity may increase or decrease depending on the properties of the matter. To understand this process it is helpful to make some defintions.

Emission

Generally material has two routes for the emission of radiation: stimulated emission and spontaneous emission. The rate of the former is proportion to the intensity of the beam so it is convenient to lump it with the absorbing properties of the material. The spontaneous emission is independent of the radiation field.

Let's define the spontaneous emission coefficient, $j$. This is the energy emitted per unit time into unit solid angle from a unit volume, so we have

$dE=jdVd\Omega dt$

and similarly

$dE=j_{\nu }dVd\Omega dtd\nu .$

If the emitter is isotropic or the emitters are randomly oriented then the total power emitted per unit volume and unit frequency is

$P_{\nu }=4\pi j_{\nu }.$

Often the emission is isotropic and it is convenient to define the emissivity of the material per unit mass

$dE=\epsilon _{\nu }\rho dVdtd\nu {\frac {\Omega }{4\pi }}$

where $\rho$ is the density of the emitting medium. $\epsilon _{\nu }$ is simply related to $j_{\nu }$ for an isotropic emitter

$j_{\nu }={\frac {\epsilon _{\nu }\rho }{4\pi }}.$

As a beam travels through the material, its intensity increases such that

${\frac {dI_{\nu }}{ds}}=j_{\nu }.$

Here is the first term in the equation of radiative transfer. We know what $I_{\nu }$ is and we will spend much of the course figuring out what $j_{\nu }$ is for different physical systems.

Absorption

The equation for absorption is similar, except that amount of absorption is proportional to the intensity of the radiation. You can't absorb radiation that isn't there.

${\frac {dI_{\nu }}{ds}}=-\alpha _{\nu }I_{\nu }.$

Phenomenologically you can imagine that there are many independent absorbs in the beam, each with a cross section $\sigma _{\nu }$ and a number density $n$. This would yield

$\alpha _{\nu }=\sigma _{\nu }n.$

It is often convenient to define $\alpha _{\nu }=\rho \kappa _{\nu }$ where $\kappa _{\nu }$ is the opacity of the material. You can think of this as the cross section per unit mass of the absorbers.

The quantity $\alpha _{\nu }$ has both positive and negative contributions. The positive contributions are true absorption and the negative ones coorespond to stimulated emission.

The Radiative Transfer Equation

Putting these equations together yields the radiative transfer equation,

${\frac {dI_{\nu }}{ds}}=-\alpha _{\nu }I_{\nu }+j_{\nu }.$

Once we know $\alpha _{\nu }$ and $j_{\nu }$ for the system of interest, it is straightforward to solve the equations of radiative transfer. We shall see a formal solution a bit later. If there is scattering as well as absorption and emission, things get a bit more complicated.

Let's look at a few examples.

• Emission only

${\frac {dI_{\nu }}{ds}}=j_{\nu }$

yields the solution

$I_{\nu }(s)=I_{\nu }(s_{0})+\int _{s_{0}}^{s}j_{\nu }(s')ds'$

The increase in brightness is simply the integral of the emission coefficient along the line of sight. This limit is also know as the optically thin regime.

• Absorption only

${\frac {dI_{\nu }}{ds}}=-\alpha _{\nu }I_{\nu }$

which yields

$I_{\nu }(s)=I_{\nu }(s_{0})\exp \left[-\int _{s_{0}}^{s}\alpha _{\nu }(s')ds'\right]$

The result for pure absorption inspires us to look at the radiative transfer equation again. Let's define,

$\tau _{\nu }=\int _{s_{0}}^{s}\alpha _{\nu }(s')ds'$

such that $d\tau _{\nu }=\alpha _{\nu }ds$

• Emission and absorption

Using this defintion we get the following equation of radiative trasnfer,

${\frac {dI_{\nu }}{d\tau _{\nu }}}=-I_{\nu }+S_{\nu }$

where

$S_{\nu }\equiv {\frac {j_{\nu }}{\alpha _{\nu }}}$

is called the source function. It has the same units as the intensity. It allows a formal solution of the transfer equation

$I_{\nu }(\tau _{\nu })=I_{\nu }(s_{0})e^{-\tau _{\nu }}+\int _{0}^{\tau _{\nu }}e^{-(\tau _{\nu }-\tau _{\nu }')}S_{\nu }(\tau _{\nu }')d\tau _{\nu }'$

If we have a source with a constant value of $S_{\nu }$, the solution is much simpler

$I_{\nu }(\tau _{\nu })=I_{\nu }(s_{0})e^{-\tau _{\nu }}+S_{\nu }\left(1-e^{-}\tau _{\nu }\right)=S_{\nu }+e^{-\tau _{\nu }}\left(I_{\nu }(0)-S_{\nu }\right).$

The intensity field approaches the source function as the optical depth increases.

Thermal Radiation

Let's imagine a blackbody enclosure, and we stick some material inside the enclosure and wait until it reaches equilibrium with the radiation field, $I_{\nu }=B_{\nu }(T)$. Now let move the material in a position the blocks our window to the enclosure. What can we say about the source function of the material?

We know that as light travels through the material the intensity field should approach the source function but we also know that the light emerging from the window must have $I_{\nu }=B_{\nu }(T)$. If it didn't, we could set up an adjacent blackbody enclosure at the same temperature and energy would flow between them. We must conclude that

$S_{\nu }=B_{\nu }(T){\rm {~for~a~thermal~emitter~(Kirchoff's~Law)}}$

Furthermore, we can look at the transfer equation that yields,

${\frac {dI_{\nu }}{d\tau _{\nu }}}=-I_{\nu }+B_{\nu }(T).$

Because $I_{\nu }=B_{\nu }(T)$ outside of the thermal emitting material and $S_{\nu }=B_{\nu }(T)$ within the material, we find that $I_{\nu }=B_{\nu }(T)$ throughout the enclosure.

If we remove the thermal emitter from the blackbody enclosure we can see the difference between thermal radiation and blackbody radiation. A thermal emitter has $S_{\nu }=B_{\nu }(T)$, so the radiation field approaches $B_{\nu }(T)$ (blackbody radiation) only at large optical depth.

Einstein Coefficients

Kirchoff's law is a relationship between the emission and absorption coefficients for a thermally emitting material, specifically $j_{\nu }=\alpha _{\nu }B_{\nu }$. This relationship suggests some connection between emission and absorption at a microscopic level. It was Einstein that first elucidated this connection.

Let's imagine a two-level atom. The lower level has energy $E$ and statistical weight $g_{1}$. You can think of the statistical weight as the number of ways that the atom can be in the particular state, the degeneracy of the state. The second level has an energy $E+h\nu _{0}$ and a statistical weight of $g_{2}$.

There are three possible transitions,

• Spontaneous Emission with probability per unit time of $A_{21}$.
• Absorption Rate of absorption is proportional to the angle-averaged intensity of the radiation field ($J_{\nu }(\nu _{0})$) times the coefficient $B_{12}$.

Technically the atom does not absorb at precisely one frequency but over a width $\delta \nu$. To simplify matters we will take $\delta \nu \rightarrow 0$ and the line profile $\phi(\nu) \rightarrow \delta(\nu-\nu_0)$.

• Stimulated Emission The transition rate for stimulated emission is $B_{21}J_{\nu }(\nu _{0})$.

For the system to be in thermodynamic equilibrium, the number of transitions from level one to two must equal the reverse transitions,

$n_{1}B_{12}J_{\nu }(\nu _{0})=n_{2}A_{21}+n_{2}B_{21}J_{\nu }(\nu _{0}).$

Let's solve for $J_{\nu }(\nu _{0})$,

$J_{\nu }(\nu _{0})={\frac {n_{2}A_{21}}{n_{1}B_{12}-n_{2}B_{21}}}.$

We know that the system is in thermodynamic equilibrium so

${\frac {n_{1}}{n_{2}}}={\frac {g_{1}\exp(-E/kT)}{g_{2}\exp(-(E+h\nu _{0})/kT)}}={\frac {g_{1}}{g_{2}}}\exp(h\nu _{0}/kT).$

Let's substitute this into the earlier result

$J_{\nu }(\nu _{0})={\frac {A_{21}}{(g_{1}/g_{2})\exp(h\nu _{0}/kT)B_{12}-B_{21}}}$

We know that since the system is in thermodynamic equilibrium with the radiation field $J_{\nu }=B_{\nu }(T)$

${\begin{matrix}{\frac {2h}{c^{2}}}{\frac {\nu ^{3}}{\exp(h\nu _{0}/kT)-1}}.&=&{\frac {A_{21}}{(g_{1}/g_{2})\exp(h\nu _{0}/kT)B_{12}-B_{21}}}\\&=&{\frac {A_{21}}{B_{21}}}{\frac {1}{(g_{1}/g_{2})\exp(h\nu _{0}/kT)B_{12}/B_{21}-1}}.\end{matrix}}$

Because the temperature $T$ may be set arbitrarily we must have the following relationships

${\begin{matrix}A_{21}&=&{\frac {2h\nu ^{3}}{c^{2}}}B_{21},\\g_{1}B_{12}&=&g_{2}B_{21}.\end{matrix}}$

Because the Einstein coefficients are properties of the atom alone, they do not depend on the assumption of thermodynamic equilibrium. They are quite powerful. If we calculate the probability of absorption of a photon for example, we can use the Einstein relations to find the rate of stimulated and spontaneous emission. This proof is an example of the principle of detailed balance of a microscopic process.

Something to think about

Can you use the principle of detailed balance to say anything about the relationship between the stimulating and the stimulated photon?

A Physical Aside: What is deep about the Einstein coefficients?

The Einstein coefficients seem to say something magical about the properties of atoms, electrons and photons. Somehow atoms are forced to behave according to these equations. It turns out that the relationships between Einstein coefficients (1917) are an example of Fermi's Golden Rule (late 1920s).

Calculating the Emission and Absoprtion Coefficients

We can write the emission and absorption coefficients in terms of the Einstein coefficients that we have just exmained. The emission coefficient $j_{\nu }$ has units of energy per unit time per unit volume per unit frequency per unit solid angle! The Einstein coefficient $A_{21}$ gives spontaneous emission rate per atom, so dimensional analysis quickly gives

$j_{\nu }={\frac {h\nu }{4\pi }}n_{2}A_{21}\phi (\nu )$

The absorption coefficent may be constructed in a similar manner

$\alpha _{\nu }={\frac {h\nu }{4\pi }}\phi (\nu )\left(n_{1}B_{12}-n_{2}B_{21}\right)$

We can now write the absorption coefficient and the source function using the relationships between the Einstein coefficients as

${\begin{matrix}\alpha _{\nu }&=&{\frac {h\nu }{4\pi }}n_{1}B_{12}\left(1-{\frac {g_{1}n_{2}}{g_{2}n_{1}}}\right)\phi (\nu )\\S_{\nu }&=&{\frac {2h\nu ^{3}}{c^{2}}}\left({\frac {g_{2}n_{1}}{g_{1}n_{2}}}-1\right)^{-1}.\end{matrix}}$

LTE

To derive these relations we have not made any assumptions about whether the photons or the matter are in thermal equilibrium with themselves or each other. An extremely useful assumption is that the matter is in thermal equilibrium at least locally (Local Thermodynamic Equilibrium). This assumption forms the basis of the theory of stellar atmospheres.

In this case the ratio of the number of atoms in the various states is determined by the condition of thermodynamic equilibrium

${\frac {n_{1}}{n_{2}}}={\frac {g_{1}}{g_{2}}}\exp \left({\frac {h\nu _{0}}{kT}}\right).$

This ratio yields the following absorption coefficient and source function

${\begin{matrix}\alpha _{\nu }&=&{\frac {h\nu }{4\pi }}n_{1}B_{12}\left(1-\exp(-h\nu _{0}/kT)\right)\\S_{\nu }&=&B_{\nu }(T)\end{matrix}}$

Something to think about

Because the source function equals the blackbody function, does this mean that sources in local thermodynamic equilibrium emit blackbody radiation?

Non-Thermal Emission

In any situation where

${\frac {n_{1}}{n_{2}}}\neq {\frac {g_{1}}{g_{2}}}\exp \left({\frac {h\nu _{0}}{kT}}\right).$

(\ie if the radiating particles do not have a Maxwellian distribution) one has to deal use the full expression for the source function; a power-law distibution oftens occurs astrophysically.

An extreme example of non-thermal emission is the maser. For atoms in thermodynamic equilibrium we have

${\frac {n_{2}g_{1}}{n_{1}g_{2}}}=\exp \left(-{\frac {h\nu }{kT}}\right)<1$

so that

${\frac {n_{1}}{g_{1}}}>{\frac {n_{2}}{g_{2}}}$

which means that the absorption coefficient is always positive in thermodynamic equilibrium. However, let us imagine a situation in which

${\frac {n_{1}}{g_{1}}}<{\frac {n_{2}}{g_{2}}}.$

This yields a negative absorption coefficient, so the optical depth decreases and becomes negative as one passes through a region with inverted populations and the intensity of the radiation actually increases expontentially as the magnitude of the optical depth increases. So we have to thank Einstein for the laser as well.

Scattering

From the preceding discussion one might think that the theory of radiative transfer simply relies the application of the formal solution using the Einstein coefficients for various processes of interest.

However, there is a big elephant in the middle of the room that we have been ignoring --- scattering. Why is scattering a problem? Couldn't you think about scattering as the absorption and re-emission of a photon and include the process in the absorption coefficients and source functions? The answer is no.

The formalism that we have developed so far doesn't allow there to be a correlation between the properties of an absorbed photon and the emitted photon. On the other hand, the initial direction and energy of a scattered photon are generally highly correlated with the photon's final momentum.

We can first look at a process in which the photon is scattered into a random direction without a change in energy. This yields an emission of

$j_{\nu }=\sigma _{\nu }J_{\nu }.$

Notice that the emission rate depends on the radiation field through $J_{\nu }$ and not solely on the properties of the scatterer through $\sigma _{\nu }$. If isotropic scattering is the only process acting we find that the source function

$S_{\nu }=J_{\nu }={\frac {1}{4\pi }}\int d\Omega I_{\nu }.$

The equation describing the evolution of the radiation field is still rather innocuous looking

${\frac {dI_{\nu }}{ds}}=-\sigma _{\nu }\left(I_{\nu }-J_{\nu }\right).$

However, it is a completely different beast. The evolution of the intensity of a particular ray depends not only the intensity of the ray and the local properties of the material but also on the intensity of all other rays passing through the same point --- we have an integro-differential equation.

If you think about things more generally, we had this same problem before introducing scattering because the properties of the emitting and absorbing material usually depend on the radiation field. Even if one neglects scattering, one often has to solve an integro-differential equation.

Random Walks

We can get an order of magnitude feeling for how much scattering will affect the radiation field emerging from a source using the concepts of the mean free path and the random walk.

The mean free path for scattering (or similarly for absorption) is simply the reciprocal of the scattering coefficient $\sigma _{\nu }$. So if we imagine a single photon travelling through the material, it will go typically a distance $l=\sigma _{\nu }^{-1}$ then change direction. The net displacement of the photon after $N$ free paths is

$\mathbf {R} =\mathbf {r} _{1}+\mathbf {r} _{2}+\mathbf {r} _{3}+\cdots +\mathbf {r} _{N}$

However, on average it is as likely to go one way as the other so the mean values of all of the $\mathbf {r} _{i}$ vectors vanishes as does the sum. Let's ask instead how far the photon typically ends up away from the starting point, here we have

$|\mathbf {R} |^{2}=|\mathbf {r} _{1}|^{2}+|\mathbf {r} _{2}|^{2}+|\mathbf {r} _{3}|^{2}+\cdots +2\mathbf {r} _{1}\cdot \mathbf {r} _{2}+2\mathbf {r} _{1}\cdot \mathbf {r} _{3}+\cdots$

All of the cross terms vanish on average if the scattering is isotropic, but $\left\langle \mathbf {r_{1}} ^{2}\right\rangle \approx l=\sigma _{\nu }^{-1}$ so the net distance travelled after $N$ scatterings is

$l_{*}^{2}=Nl^{2},l_{*}={\sqrt {N}}l.$

If some blob of gas has a typically dimension $L$ we can estimate the number of scatterings through the gas to be $N\approx L^{2}/l^{2}$. This is why people sometimes say that it takes a million years for a photon to escape the sun.

In general if $\tau$ is large the average number of scatterings $N\approx \tau ^{2}$ while for $\tau \ll \ 1$, $N\approx \tau$

Combined Scattering and Absorption

In general a material can both scatter and absorb photons. In this case the transfer equation has two terms. Let's focus on coherent isotropic scattering and thermal emission and get

${\begin{matrix}{\frac {dI_{\nu }}{ds}}&=&-\alpha _{\nu }\left(I_{\nu }-B_{\nu }\right)-\sigma _{\nu }\left(I_{\nu }-J_{\nu }\right)\\&=&-\left(\alpha _{\nu }+\sigma _{\nu }\right)\left(I_{\nu }-S_{\nu }\right)\end{matrix}}$

where

$S_{\nu }={\frac {\alpha _{\nu }B_{\nu }+\sigma _{\nu }J_{\nu }}{\alpha _{\nu }+\sigma _{\nu }}}$

The net absorption coefficient is $\alpha _{\nu }+\sigma _{\nu }.$ On average a photon will travel a distance

$l_{\nu }={\frac {1}{\alpha _{\nu }+\sigma _{\nu }}}$

before it is absorbed or scattered. The chance that the free path will end in absorption is

$\epsilon _{\nu }={\frac {\alpha _{\nu }}{\alpha _{\nu }+\sigma _{\nu }}}$

and the chance that it will be scattered is

$1-\epsilon _{\nu }={\frac {\sigma _{\nu }}{\alpha _{\nu }+\sigma _{\nu }}}.$

We can rewrite the source function as

$S_{\nu }=\left(1-\epsilon _{\nu }\right)J_{\nu }+\epsilon _{\nu }B_{\nu }.$

After a photon is emitted it may bounce around several times before it is absorbed; the average number of scatterings per absorption is $N=\epsilon _{\nu }^{-1}$. After these $N$ scatterings it will typically have travelled a distance,

$l_{*}={\sqrt {N}}l={\frac {1}{\sqrt {\alpha _{\nu }(\alpha _{\nu }+\sigma _{\nu })}}}$

$l_{*}$ is the typically distance between the points of creation and destruction of a photon -- it is called the diffusion length, the thermalization length, or the "effective mean free path". If the material has some thickness $L$, we can define the "effective optical depth of the material to be $\tau _{*}=L/l_{*}$.

If $\tau _{*}$ is small, then a photon after being created in the medium, bounces around until it emerges (it is usually not absorbed). In this case the power emitted by material will simply be the

${\mathcal {L}}_{\nu }=4\pi \alpha _{\nu }S_{\nu }V,~~~(\tau _{*}\ll 1)$

where $S_{\nu }$ is the source function without scattering and $V$ is the volume of the material. If $\tau _{*}\ll 1$ the material is said to be effectively thin or translucent.

On the other hand, if $\tau _{*}\gg 1$, the medium is said to be effectively thick. In this case only photons emitted within $l_{*}$ of the surface typically escape without being absorbed. We can estimate the power emitted by

${\mathcal {L}}_{\nu }=4\pi \alpha _{\nu }B_{\nu }Al_{*}=4\pi {\sqrt {\epsilon _{\nu }}}B_{\nu }A,~~~(\tau _{*}\gg 1)$

Radiative Diffusion

We have used the random walk arguments to show that the radiation field approaches a blackbody within a few effective mean paths (or thermalization lengths) of the surface. Furthermore, the radiation field becomes isotropic within a mean free path of the surface. We will first look at the first situation in which the radiation field is approximately a blackbody.

Rosseland Approximation

Because stellar atmospheres (i.e. the effective mean path) are generally thin compared to the size of the star, we can assume that this region has plane parallel symmetry, that is that the properties of the material depend only on the depth from the surface $z$. The intensity will generally depend on the depth and the angle that the ray makes with the normal $\theta$. It is generally convenient to use $\mu =\cos \theta$ instead of $\theta$ itself.

${\frac {\partial I_{\nu }(z,\mu )}{ds}}=\cos \theta {\frac {\partial I_{\nu }(z,\mu )}{\partial z}}=\mu {\frac {\partial I_{\nu }(z,\mu )}{ds}}=-\left(\alpha _{\nu }+\sigma _{\nu }\right)\left(I_{\nu }-S_{\nu }\right).$

Let's rearrange this as

$I_{\nu }(z,\mu )=S_{\nu }-{\frac {\mu }{\alpha _{\nu }+\sigma _{\nu }}}{\frac {\partial I_{\nu }}{\partial z}}.$

Here comes the assumption. Let us assume that the properties of the radiation field do not change much over a mean free path so the second term is much smaller than the first; therefore;

$I_{\nu }^{(0)}(z,\mu )\approx S_{\nu }^{(0)}(T).$

Because this is independent of the angle, $J_{\nu }^{(0)}=S_{\nu }^{(0)}(T)$, so $S_{\nu }^{(0)}=B_{\nu }$. Let's get a better approximation to the radiation field

$I_{\nu }^{(1)}(z,\mu )\approx B_{\nu }(T)-{\frac {\mu }{\alpha _{\nu }+\sigma _{\nu }}}{\frac {\partial B_{\nu }}{\partial z}}.$

Let's calculate the total flux of the radiation field.

${\begin{matrix}F_{\nu }(z)&=&\int I_{\nu }^{(1)}\cos \theta d\Omega =-2\pi {\frac {\partial B_{\nu }}{\partial z}}{\frac {1}{\alpha _{\nu }+\sigma _{\nu }}}\int _{-1}^{+1}\mu ^{2}d\mu \\&=&-{\frac {4\pi }{3}}{\frac {1}{\alpha _{\nu }+\sigma _{\nu }}}{\frac {\partial B_{\nu }}{\partial z}}=-{\frac {4\pi }{3}}{\frac {1}{\alpha _{\nu }+\sigma _{\nu }}}{\frac {\partial B_{\nu }}{\partial T}}{\frac {\partial T}{\partial z}}\end{matrix}}$

We can integrate this over all frequencies to find the total flux

$F(z)=\int _{0}^{\infty }F_{\nu }(z)d\nu =-{\frac {4\pi }{3}}{\frac {\partial T}{\partial z}}\int _{0}^{\infty }\left(\alpha _{\nu }+\sigma _{\nu }\right)^{-1}{\frac {\partial B_{\nu }}{\partial T}}d\nu .$

Unfortunately the integral above generally cannot be done analytically. However, we can elucidate some of its properties. First, the absorption and scattering coefficients are summed harmonically so regions of the spectrum that have the least absorption or scattering will dominate the energy flow. Furthermore, the harmonic sum is weighted heavily in the region where $\partial B_{\nu }/\partial T$ is large, near the peak of the blackbody emission.

One can define a mean absorption coefficient by

${\frac {1}{\alpha _{R}}}\equiv {\frac {\int _{0}^{\infty }\left(\alpha _{\nu }+\sigma _{\nu }\right)^{-1}{\frac {\partial B_{\nu }}{\partial T}}d\nu }{\int _{0}^{\infty }{\frac {\partial B_{\nu }}{\partial T}}d\nu }}={\frac {\int _{0}^{\infty }\left(\alpha _{\nu }+\sigma _{\nu }\right)^{-1}{\frac {\partial B_{\nu }}{\partial T}}d\nu }{\frac {4\sigma T^{3}}{\pi }}}$

If we substitute this into the earlier expression we get

$F(z)=-{\frac {16\sigma T^{3}}{3\alpha _{R}}}{\frac {\partial T}{\partial z}}.$

where $\alpha _{R}$ is the Rosseland mean absorption coefficient. In stellar astrophysics one often uses the column density $\Sigma$ as the independent variable rather than $z$ -- $d\Sigma =\rho dz$. Making the substitution yields

$F(z)=-{\frac {16\sigma T^{3}}{3\alpha _{R}}}\rho {\frac {\partial T}{\partial \Sigma }}.=-{\frac {16\sigma T^{3}}{3\kappa _{R}}}{\frac {\partial T}{\partial \Sigma }}.$

where $\kappa _{R}=\alpha _{R}/\rho$ is the Rosseland mean opacity.

Eddington Approximation

What if you are interested in the translucent upper layers of the atmosphere within a few effective mean paths of the surface but still a few mean free paths (scattering lengths) away from the surface. In this region, the radiation field is nearly isotropic, but it need not be close to a blackbody distribution.

Because the intensity is close to isotropic we can approximate it by

$I_{\nu }(z,\mu )=a_{\nu }(z)+\mu b_{\nu }(z)\mu .$

Let's use the first three moments of the intensity

${\begin{matrix}J_{\nu }&\equiv &{\frac {1}{2}}\int _{-1}^{+1}Id\mu =a_{\nu },\\H_{\nu }&\equiv &{\frac {1}{2}}\int _{-1}^{+1}\mu Id\mu ={\frac {b_{\nu }}{3}},\\K_{\nu }&\equiv &{\frac {1}{2}}\int _{-1}^{+1}\mu ^{2}Id\mu ={\frac {a_{\nu }}{3}}\end{matrix}}$

$J$ is the mean intensity and $H$ and $K$ are proporptional to the flux and the radiation pressure. The Eddington approximation is the result that

$K={\frac {1}{3}}J$

which we found earlier to hold for strictly isotropic radiation fields. Here we find that it also holds for anisotropic radiation fields of the form defined earlier.

Let's define the normal optical depth,

$d\tau _{\nu }=-\left(\alpha _{\nu }+\sigma _{\nu }\right)dz$

yielding the radiative transfer equaition

$\mu {\frac {\partial I_{\nu }}{\partial \tau }}=I_{\nu }-S_{\nu }$

where

$S_{\nu }={\frac {\alpha _{\nu }B_{\nu }+\sigma _{\nu }J_{\nu }}{\alpha _{\nu }+\sigma _{\nu }}}.$

The source function $S_{\nu }$ is isotropic, so let's average the radiative transfer equation over direction to yield

${\frac {\partial H_{\nu }}{\partial \tau }}=J_{\nu }-S_{\nu }$

Let's also average the radiative transfer equation times $\mu$ over direction to yield

${\frac {\partial K_{\nu }}{\partial \tau }}={\frac {1}{3}}{\frac {\partial J_{\nu }}{\partial \tau }}=H_{\nu }$

Something to think about

What happen to $S_{\nu }$ in the equation above?

We can combine the two equations to yield

${\frac {1}{3}}{\frac {\partial J_{\nu }}{\partial \tau }}=J_{\nu }-S_{\nu }$

and using the definition of the source function gives

${\frac {1}{3}}{\frac {\partial ^{2}J_{\nu }}{\partial \tau ^{2}}}=J_{\nu }-{\frac {\alpha _{\nu }B_{\nu }+\sigma _{\nu }J_{\nu }}{\alpha _{\nu }+\sigma _{\nu }}}=\epsilon _{\nu }\left(J_{\nu }-B_{\nu }\right).$

This is sometimes called the radiative diffusion equation. If you know the temperature structure of the material you can solve the equation for the mean intensity $J_{\nu }$ and then you know the source function $S_{\nu }$ explicitly and you can use the formal solution to the radiative transfer equation to get the radiation field.

Stellar Atmospheres

Reading Assignment

Chapter 8 of Stellar-Astrophysics Notes

Introduction

Inside the star you only needed the state variables: $P,T,\rho$ as a function of position and you tacitly assumed that everything is in thermodynamic equilibrium locally.

Stellar spectra would be really uninteresting if this worked all of the way out. In the atmosphere the mean-free path for a photon is longer or similar to the distance to open space. The optical depth to infinity is small. Therefore, we need to keep track of the photon distribution in energy, direction and polarization too. In principle, the matter need not be in thermodynamic equilibrium either.

1. Calculate the radiation field given the atmosphere structure.
2. Correct the atmosphere structure so energy is conserved throughout.
3. Repeat until converged.

• Breakdown of strict thermodynamic equilibrium
• Assumption of LTE: matter in TE, but photons are not.
• Continuum is assumed to determine the structure and spectral lines form on top.
• Atmosphere is thin; little mass (but think about red giants)

${\frac {dP}{dr}}=-{\frac {GM(r)\rho }{r^{2}}}=-g\rho$

and

${\frac {dF}{dr}}=0$

so $F=\mathrm {constant} =\sigma T_{e}^{4}$. Two important parameters:

1. $g={\frac {GM}{R^{2}}}$ and
2. $T_{e}^{4}={\frac {L}{4\pi R^{2}}}$.

To follow the photon distribution you need to use the equations of radiative transfer.

Schwarzschild-Milne Integral Equations

Using this let's develop the Schwarzschild-Milne Integral Equations

$S_{\nu }=\epsilon _{\nu }B_{\nu }+(1-\epsilon _{\nu })J_{\nu }$

where

$\epsilon _{\nu }={\frac {\alpha _{\nu }}{\alpha _{\nu }+\sigma _{\nu }}}.$

N.B. $\alpha _{\nu }$ deals with true absorption and $\sigma _{\nu }$ deals with scattering.

Let's split the radiation into outgoing and ingoing

$J_{\nu }={\frac {1}{2}}\int _{0}^{1}I(+\mu ',\tau _{n}u)d\mu '+{\frac {1}{2}}\int _{0}^{1}I(-\mu ',\tau _{n}u)d(-\mu ')$

so

$J_{\nu }={\frac {1}{2}}\int _{0}^{1}\left[\int _{\infty }^{\tau _{\nu }}S(t)e^{(\tau _{n}u-t)/\mu '}{\frac {dt}{\mu '}}\right]d\mu '+{\frac {1}{2}}\int _{0}^{1}\left[\int _{0}^{\tau _{\nu }}S(t)e^{(\tau _{n}u-t)/\mu '}{\frac {dt}{\mu '}}\right]d\mu '$

and

$J_{\nu }={\frac {1}{2}}\int _{0}^{\infty }S(t)\left[\int _{0}^{1}e^{|\tau _{\nu }-t|/\mu '}{\frac {d\mu '}{\mu '}}\right]dt.$

If we define the exponential integral

$E_{n}(z)=\int _{1}^{\infty }{\frac {e^{-zt}}{t^{n}}}dt=\int _{0}^{1}e^{-z/y}y^{n-2}dy,$

we have

$J_{\nu }(\tau _{n}u)={\frac {1}{2}}\int _{0}^{\infty }S(t)E_{1}|\tau _{\nu }-t|dt$

and

$S_{\nu }(\tau _{\nu })=\epsilon _{\nu }B_{\nu }(T(\tau _{\nu }))+(1-\epsilon _{\nu }){\frac {1}{2}}\int _{0}^{\infty }S(t)E_{1}|\tau _{\nu }-t|dt$

Limb Darkening

$I(\mu ,0)=\int _{0}^{\infty }S(t)e^{-t/\mu }{\frac {dt}{\mu }}={\frac {1}{\mu }}{\mathcal {L}}_{1/\mu }\left[S(t)\right].$

so if $S(t)=at+b$, $I(\mu ,0)=a\mu +b$.

Spectral Lines

Spectral lines form one of the most powerful diagnostics of a star's atmosphere.

The Voigt profile is a line profile resulting from the convolution of two broadening mechanisms, one of which alone would produce a Gaussian profile (usually, as a result of the Doppler broadening), and the other would produce a Lorentzian profile. Voigt profiles are common in many branches of spectroscopy. Due to the computational expense of the convolution operation, the Voigt profile is often approximated using a pseudo-Voigt profile.

Without loss of generality, we can consider only centered profiles, which peak at zero. The Voigt profile is then a convolution of a Lorentz profile and a Gaussian profile:

$V(x;\sigma ,\gamma )=\int _{-\infty }^{\infty }G(x';\sigma )L(x-x';\gamma )\,dx',$

where x is the shift from the line center, $G(x;\sigma )$ is the centered Gaussian profile:

$G(x;\sigma )\equiv {\frac {e^{-x^{2}/(2\sigma ^{2})}}{\sigma {\sqrt {2\pi }}}},$

and $L(x;\gamma )$ is the centered Lorentzian profile:

$L(x;\gamma )\equiv {\frac {\gamma }{\pi (x^{2}+\gamma ^{2})}}.$

The Gaussian results from the temperature of the gas and the Lorentzian results from the collision rate in the gas, so a spectral line provides a estimate of both the temperature and density of the atmosphere. Furthermore, if the star is also rotating, this will also broaden the lines further.

To account for the strength of a spectral line, there are several conventions.

A diagram indicating the equivalent width corresponding to the absorption line, which is shown in red.

The residual flux and residual intensity are defined with respect to the continuum surrounding the line,

$f_{\nu }(\mu )\equiv {\frac {I_{\nu }(\mu ,0)}{I_{c}(\mu ,0)}}\equiv \mathrm {residual~intensity}$

and

$r_{\nu }\equiv {\frac {F_{\nu }(0)}{F(0)}}\equiv \mathrm {residual~flux} .$

The equivalent width of a spectral line is a measure of the area of the line on a plot of intensity versus wavelength. It is found by forming a rectangle with a height equal to that of continuum emission, and finding the width such that the area of the rectangle is equal to the area in the spectral line.

Formally, the equivalent width is given by the equation

$W_{\lambda }=\int (1-F_{\lambda }/F_{0})d\lambda$.

Here, $F_{0}$ represents the continuum intensity on either side of the absorption or emission feature, while $F_{\lambda }$ represents the intensity across the entire wavelength range of interest. Then $W_{\lambda }$ represents the width of a hypothetical line which drops to an intensity of zero and has the "same integrated flux deficit from the continuum as the true one." This equation can be applied to either emission or absorption, but when applied to emission, the value of $W_{\lambda }$ is negative, and so the absolute value is used.

Schuster-Schwarzschild Model

Sketch of Schuster-Schwarzschild model for line formation

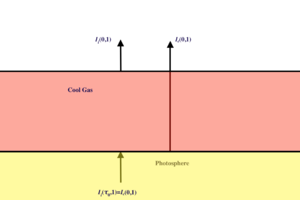
This is based on the Eddington approximation and we assume that the lines are actually scattering lines. The gas immediately radiates the energy in a different direction, so we have

$\mu {\frac {dI_{v}}{d\tau _{\nu }}}=I_{\nu }-J_{\nu }$

and

$d\tau _{\nu }=-\sigma _{\nu }dx$

Because the scatter is isotropic the flux is conserved. If we average the radiative transfer equation over direction

${\frac {dH_{\nu }}{d\tau _{\nu }}}=J_{\nu }-J_{\nu }=0$

and because $H_{\nu }\propto F_{\nu }$, the flux is conserved. Let's take $I_{\nu }=a_{\nu }(z)+\mu b_{\nu }(z)$ so

$J_{\nu }=a_{\nu },H_{\nu }={\frac {b_{\nu }}{3}},K_{\nu }={\frac {a_{\nu }}{3}},$

${\frac {dK_{\nu }}{d\tau _{\nu }}}={\frac {1}{3}}{\frac {dJ_{\nu }}{d\tau _{\nu }}}=H_{\nu }$

and

${\frac {dJ_{\nu }}{d\tau _{\nu }}}=b_{\nu }.$

We can solve these equations

$I_{\nu }^{l}(\tau ,\nu )=b_{\nu }(\tau _{\nu }-\tau _{0})+b_{\nu }\mu +Q$

at $\tau _{\nu }=\tau _{0}$ and $\mu =1$, $I_{\nu }^{l}(\tau _{0},1)=I_{\nu }^{c}(0,1)$, so $Q=I_{\nu }^{c}(0,1)-b_{\nu }$.

Putting it all together yields

$I_{\nu }^{l}(\tau ,\mu )=b_{\nu }(\tau _{\nu }-\tau _{0})+b_{\nu }\mu +I_{\nu }^{c}(0,1)-b_{\nu }.$

On the outer surface ($\tau _{\nu }=0$) there is no incoming intensity so

$I_{\nu }^{l}(0,-1)=0=b_{\nu }(-\tau _{0})-b_{\nu }+I_{\nu }^{c}(0,1)-b_{\nu },$

$b_{\nu }(2+\tau _{0})=I_{\nu }^{c}(0,1)$

and

$I_{\nu }^{l}(\tau ,\mu )=I_{\nu }^{c}(0,1)\left[{\frac {\tau _{\nu }+(\mu +1)}{2+\tau _{0}}}\right].$

Therefore, the residual intensity and flux are given by

$f_{\nu }={\frac {\mu +1}{\tau _{0}+2}},r_{\nu }={\frac {2}{\tau _{0}+2}}$

Assignment

Assume the following:

• The Rosseland mean opacity is related to the density and temperature of the gas through a power-law relationship,

$\kappa _{R}=\kappa _{0}\rho ^{\alpha }T^{\beta };$

• The pressure of the gas is given by the ideal gas law;
• The gas is in hydrostatic equilibrium so $p=g\Sigma$ where $g$ is the surface gravity; and
• The gas is in radiative equilibrium with the radiation field so the flux is constant with respect to $z$ or $\Sigma$.

Calculate the temperature of the gas as a function of $\Sigma$ for a general opacity law.

Now use the specific opacity law

$\kappa _{R}=3.68\times 10^{22}g_{ff}(1-Z)(1+X){\frac {\rho }{1~\mathrm {g~cm} ^{3}}}\left({\frac {T}{1\mathrm {K} }}\right)^{-7/2}\mathrm {cm} ^{2}\mathrm {g} ^{-1}$

and take the value of the gravitational acceleration and effective temperature appropriate for the Sun to get an estimate for the run of temperature with column density for the Sun.

Now let's try to estimate the continuum spectrum under the following assumptions

• The opacity is a power-law function of wavelength: $\kappa _{\nu }\propto \nu ^{-\delta }$.
• The emission from the atmosphere is thermal.
• The radiation is coupled to the atmosphere at optical depths $\tau _{\nu }$ greater than unity and completely decoupled at shallower depths where $d\tau _{\nu }=\kappa _{\nu }d\Sigma /(\cos \theta )$.

What does the spectrum ($I_{\nu }$) look like for $\delta =0$ as a function of $\theta$? What about $\delta =2$ and $\delta =3$?

Winds

Winds of Main-Sequence Stars

Winds of Post-Main Sequence Stars

• 
• 
• 
• 

Molecules

Assignment

Part 1

The young white dwarfs in the globular cluster 47 Tuc have a mass of 0.53 solar masses. The turn-off stars (those leaving the main sequence now) have a mass of 0.9 solar mass. The metallicity of 47 Tuc is 0.0033. Use 1MS_prems_towd Can you find values of the wind parameters

  Reimers_wind_eta
  Blocker_wind_eta 

that yield the initial-final mass relation for 47 Tuc? Are these values unique? What is different about choosing different values, if there is a difference? How could you tell what the stars are actually doing?

Part 2

Write your own run_star_extras.f so that you can vary the neutrino production rates by a constant factor that you can give in your inlist file.

Compact Objects

Reading Assignment

Chapter 6 of Collins, George W. (1989), The Fundamentals of Stellar Astrophysics, Freeman, ISBN 0-7167-1993-2, PDF

Assignment

Part 1: White-Dwarf Cooling

You will use the output from the one-solar-mass star that you did in week 2 to look at white-dwarf cooling. Unfortunately, the program stopped when the luminosity was less than one-tenth of solar, so you will have to restart the calculation where you left off. To do this

• Copy the directory with your results so far using the following command:

 cp -rp 1M_pre_ms_to_wd 1M_pre_ms_to_wd_continued

• In the new directory, rename final.mod to restart.mod using

 mv final.mod restart.mod

• Edit the inlist_1.0 file to use the restart.mod to start. Delete the following line

     create_pre_main_sequence_model = .true.

• Add the following lines

     load_saved_model = .true.
     saved_model_name = 'restart.mod'

• Set log_L_lower_limit = -6 in the inlist_1.0 file.
• Run the new model.

You will find that the history file literally starts where you left off. The model numbers and times are sequential, so you can combine the two history files without too much trouble. Furthermore, the new run will also add new profile files ... it will not overwrite the old ones.

Using the combined history file, I would like for you to construct the cooling curve for the white dwarf in the V-band, so on the x-axis you will have the base-ten logarithm of the age of the white dwarf and on the y-axis you will have the absolute V magnitude. You should define the time of birth of the white dwarf to coincide the local maximum in the luminosity on the AGB.

Also construct the cooling curve using the total luminosity. You should observe several slopes in this cooling curve. Identify the dominant process in each regime, using what you learned in class.

Part 2: Neutron-Star Accretion

You will be looking at the following models in the test_suite: ns_h and ns_he. You will need to change the frequency of the history file output because we will want high time resolution, so change history_interval to 1 in both of the inlists. You can also decrease profile_interval too, if you want to look at the structure of the burning layers for yourself. I would like you to plot luminosity versus time for both of the models and answer the following questions for hydrogen and helium accretion.

1. What is the rise time of the burst?
2. How does the luminosity change after the initial rise?
3. What is the duration of the plateau of the burst, if there is one?
4. What is the decay time after the burst?

Finally speculate why the behaviour is so different using what you know about hydrogen and helium burning.