Communicating Science/Communicating Uncertainty
General audiences may hold the misconception that STEM disciplines are all about proofs, where scientists perform experiments to prove hypotheses or theories. However, In STEM disciplines, the vast majority of conclusions are based on measures of probability; researchers decide on a level of uncertainty that they are happy to accept before concluding one way or another what their data show (Fischhoff and Davis, 2014).
Here are some reasons for uncertainty in STEM:
- There are many different ways of approaching any research question, conducting experiments, and interpreting data/results. Even when two researchers view the same results, they might not interpret them the same way.
- The production of knowledge is an ongoing, dynamic process. Uncertainty provides opportunities for collaborative knowledge production and ongoing conversations.
- STEM research often forms conclusions based on the probability/likelihood of an explanation for what causes the results being the correct one. Much STEM research is never certain, which means it is important to indicate the degree of confidence held in a particular result (e.g. your new drug might have resulted in a statistically significant reduced chance of getting sick, but that does not mean that it will be 100% effective for everyone that takes it…).
In academic writing, researchers often use hedging language to convey uncertainty. Hedging is a kind of cautious language that conveys uncertainty, tentativeness, or hesitancy in a claim (Cüneyt, 2018). Hedging involves using words such as “could,” “might,” “may,” “often,” “possibly,” and others and allows an author to qualify a claim to protect themselves from outright refutation that an expert audience might raise.
Consider the following two examples:
Here, the researchers are able to put forth a claim for consideration about the importance of their research. Not only does the inclusion of this hedging term make their claim less universal, it opens up the possibility for future research.
Now, consider how removing the hedging term changes the sentence:
The degree of certainty in this second sentence changes considerably, making it much easier to refute.
Communicating uncertainty is also an important skill when communicating with non-specialists. We have identified five strategies that you can put into practice when communicating uncertainty to boost the chances of your readers understanding the level of uncertainty. You can:
- Make any numbers (and statistical analyses) easy to interpret.
- Contextualize these with an everyday comparison.
- Choose descriptive language very carefully.
- Use figures and images as well as words and numbers.
- Communicate timelines (when might new data be available?).
Making Numbers (and Statistical Analyses) Easy to Interpret
When dealing with very large or very small numbers, it is a good idea to round these up/down to make it easier for people to picture.
An Example
If something has a 4,427-1 chance of happening, it’s fine to tell people that there is ‘roughly a 4,500-1 chance.’ However, if something has an 8.3/1 chance of happening, telling someone that there is ‘roughly a 10/1 chance,’ is misleading because there is actually a reasonably large difference between the two.
Watch out for related contingencies (e.g. when one thing affects another, make sure you state the chance based on the combined likelihood, as well as the individual ones). For example, if I have a 10% chance of winning a regional award based on my grades, and then a 20% chance of winning a national award, it should be made clear that I only have a 2% chance of winning the national one (0.1 x 0.2 = 0.02).
It is also important to avoid framing bias when working with numbers. Framing bias can cause people to home in on the wrong message, and is often linked to your choice of wording, or even in the order that you introduce things.
An Example
Suppose there is a 10/1 chance that people will have a reaction to a new immunization that will make you feel very poorly for a few days, but that it is important to have the jab as catching the disease without immunization could be much worse.
If you tell people that ‘anyone having a reaction will feel very poorly and 1 in 11 of you will have this reaction,” you are focusing on the negative possibility and could dissuade people from having the immunization.
You should instead say something like ‘being able to protect ourselves from this disease is very important, so although there is a 10% chance that you might have a reaction that could make you feel poorly for a few days, medical staff are recommending this jab.’
Contextualizing Numbers with Everyday Comparisons
This is not always appropriate, but it can help to put things into context and make people understand the likelihood of something happening more easily. Pay special attention to your audience and try to tailor a comparison to them.
An Example
If you are speaking to members of a poker society, and want to communicate that there is an approximate 2% chance of another immunization making people feel poorly for a few days, you could try to relate this to an everyday example they will understand by saying something like ‘The chance of having a reaction to the jab and feeling poorly is very similar to your chances of drawing the Ace of hearts from a standard deck of cards with only one go.’ This works because there are 52 cards in a deck (and only one ace of hearts, which means the chances of drawing it are 1.92%).
Choosing Appropriate Descriptive Language
This links in fairly closely to the idea of avoiding framing bias; if you tell people that ‘the reaction to this jab that some people have is horrifying; you’ll feel gross for days,’ they will be more likely to focus on this and ignore the probability of actually being affected. People will also interpret horrifying and gross very differently, and this is the key to choosing appropriate descriptive language. Be very careful when using adjectives that imply a quantitative element to what you are saying.
An Example
If you said the chance of having a reaction to the second immunization was pretty unlikely, your readers would likely interpret this very differently. What does ‘pretty unlikely’ mean? One person might assume there is a 20-30% chance of something ‘pretty unlikely’ happening, whereas another might think this means there is only a 2-5% chance of it happening.
For this reason, it is always a good idea to use objective adjectives where possible, and to accompany them with a distinct number (e.g. ‘There is a 2% chance that you will have a reaction to this immunization, so it’s pretty unlikely.’).
Using Figures and Images (as well as Words and Numbers)
Some people find it easier to visualize and interpret patterns when they see them in figures and images instead of reading about them in print. The great advantage that figures have over words and numbers is that they can be more effective in highlighting magnitudes of differences between comparisons.
There are a few tips that you should put into practice when producing effective figures (such as keeping them simple, avoiding white space, and using bar graphs where possible – these are easier to interpret than pie charts and scatter plots). These tips and more information can be found by visiting our Effective Tables and Figures resource.
An Example
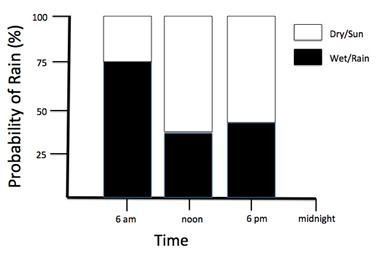
If you write that there is a 75% chance of rain at 6 am on a particular day, then a 35% chance of rain at noon, and a 40% chance at 6 pm, it is not easy to quickly relate to the relative uncertainty of these estimates; how much of a difference is there in these estimates?
The figure below makes this much easier to visualize, and might help you make a more informed decision as to whether you would risk going out without a rain jacket at certain points of the day.
Communicating Timelines
Because scientific knowledge is constantly evolving, it is a good idea to mention whether there will be an update in the coming weeks/months/years that might change the information you are currently presenting.
It is also a good idea to inform people when they can expect to hear more information in the midst of a crisis. For example, if there is an outbreak of mumps at school, it is better to tell people that you are unsure of the risk their children have of catching it if you don’t know, but that you are working with health specialists and will have information on this for them in the next five days. Telling them that ‘we don’t know’, but not giving them an indication of when you will know more is only going to cause worry and anger.
An Example
You might have completed Stage One of a research project that shows there is a 1 in 2,000 chance that your town will be hit by an earthquake in the next 10 years. However, if Stage Two is currently underway and you will have additional data to provide a more accurate estimate in three months, you should tell people that; not only are you underlining the point that your estimate at present is just that – an estimate – but you are also giving them a timeline as to when they can expect to get a more fine-grained one.
Communicating Uncertainty Quick Quiz
1) Read the following summary of some research in which you must communicate the degree of uncertainty in your results.
We have assessed the risk of a serious volcanic eruption affecting people living in the nearest town and believe there is a 1 in 151,091 chance that such an eruption will occur in the next week, a 1 in 106 chance in the next 10 years and is a 1 in 12 chance that it will happen in the next 50 years.
a) Decide whether you can simplify the three numbers without affecting their accuracy too much, to make this easier for people to interpret, and then make these simplifications if you think it is possible to do so (1 mark for each decision, 3 marks total).
b) Read the following descriptions of the risk facing town residents, and rank these in order from best to worst, remembering the importance of avoiding framing bias (4 marks):
- A: Realistically, there is no chance that the volcano will erupt in the next week.
- B: It is a bit more likely that the volcano will erupt by 2065 than by 2025.
- C: It is very unlikely that the volcano will erupt in the next 50 years.
- D: There is an absolutely tiny chance that the volcano will erupt in the next week.
2) Read the three short descriptions below that all deal with scientific uncertainty in some way. Try to suggest what the potential problems are with each one and then re-write them to remove these problems (3 marks).
i) If the pest outbreak spreads to the city, there is a 1.3% chance that all the maple trees will die. Scientists think there is approximately a 14% chance that it will reach the city.
ii) Statistics show that cyclists involved in traffic accidents have a 45% chance of missing at least two weeks of work to recover from injuries. Car drivers have only a 15% chance, but on average they are involved in six times as many accidents.
iii) Every single one of our 150 test subjects improved their performance in biology exams following our instructional course, so there is no chance that you would pay for it and not see an improved result at the end of term.
Quick Quiz Answer Key
To check your answers and see whether you are now a wizard at communicating uncertainty effectively in your science writing, you should access the answer key here.