Collaborative Filtering on Movie Lens Dataset

Collaborative Filtering on Movie Lens Dataset

This page applies a matrix factorization collaborative filtering model to different subsets of the movie lens dataset to test how the type of data used to train the model affects model performance.

Principal Author: Katherine Breen

Abstract

This page compares how different training data affects collaborative filtering model performance and tests the hypothesis that including more information in training data will result in better model performance. This page applies a matrix factorization algorithm to create a collaborative filtering model that predicts user movie ratings. The model is trained on three different datasets with different amounts and types of information. The first model is trained using 30 hidden features using user ratings. The second model is trained on 49 hidden features with 19 of them fixed to represent movie genres. The third model is trained on 30 hidden features with 19 of them fixed to represent movie genres. This page finds the third model to be the most successful when measuring performance through average sum of square error.

Builds on

This page builds on information from the collaborative filtering page.

Related Pages

A couple other pages on this wiki have covered collaborative filtering. This page looks at a different method of collaborative filtering using singular value decomposition and restricted Boltzmann machines. This page describes different methods for matrix factorization for recommender systems and looks at papers that have applied this to a Netflix dataset.

Content

Background

Recommender systems are widely used by platforms to suggest websites, movies, and products based on previous customer data. A popular example of a platform that uses recommender systems is Amazon. When a customer searches for a product, Amazon will suggest the most relevant products to that customer based on their search and other data. Amazon uses a recommender system to choose which products are most relevant to a customer. Recommender systems are trained on user data. This data can include a variety of information such as product information, user information and user ratings. While a recommender system will not have complete information for a single user (ie. a user will not rate every single product available), with enough information the system can make recommendations based on data from users with similar interests.

Many recommendation algorithms use collaborative filtering to suggest products . Collaborative filtering looks for relationships between users and products and maps those into a latent space. This helps capture patterns between users and relevant products, allowing the recommender system to suggest products a user may like based on preferences of users with similar interests.

This page applies a matrix factorization collaborative filtering model to a movie rating dataset to predict user ratings. This page looks at how the type of data used in collaborative filtering affects the performance of the model.

Data

The data used on this page comes from the movie lens dataset . This dataset contains 100,000 ratings from 1000 users on 1700 movies. Each user has rated at least 20 movies. The ratings ranged from 1 to 5 and the average overall rating was 3.35. For each user there is information on occupation, location, age and gender. For each movie, there is information on release date, title, and genre. There are 19 possible genres a movie can be categorized as. This page uses the user ratings as well as movie genres.

Methods

For this project, I created three different matrix factorization models:

1. Model trained on user ratings with 30 hidden features
2. Model trained on user ratings and movie genre information with 49 hidden features (19 fixed for movie genres)
3. Model trained on user ratings and movie genre information with 30 hidden features (19 fixed for movie genres)

The matrix factorization method applied maps users and items into a joint latent factor space. In this space, the user-item interactions are modelled as inner products. This is modelled with the following equation:

$f(z,w)=\Sigma _{(u,i)\epsilon k}(r_{u,i}-q_{i}^{T}p_{u})^{2}+\lambda (\|q_{i}\|^{2}+\|p_{u}\|^{2})$ where ${\hat {r}}_{u,i}=q_{i}^{T}p_{u}$

In this equation each user $u$ is associated with a vector $p_{u}$ and each item $i$ is associated with a vector $q_{i}$. The elements in the vectors measure the extent of which the item or user possesses those factors. $k$ is the set of user and item pairs for which ${\hat {r}}_{u,i}=q_{i}^{T}p_{u}$ is known. There is also a regularization term, represented by $\lambda$. The model learns by fitting to known information, like previous ratings, and then uses that information to predict future ratings for a user. The models were fit using stochastic gradient descent.

To provide a baseline, the average sum of squares error if the models just predict the mean rating is 1.26 on the training set and 1.39 on the testing set. I hypothesized that all models would outperform the baseline. Additionally, I hypothesized that the model with the most hidden features would perform the best.

Results

At first, all three models were trained over 50 epochs with $\lambda$ = 1. With 50 epochs, all the models became overfit and ended up performing similarly to the baseline. For all three models, the testing error decreased over the epochs until epoch 20 was reached. Then the model started to greatly overfit and the testing error began to decrease.

To determine the best regularization parameter, trained 40 models for each different model identified in the methods section. The 40 models were trained with different lambda values ranging from 1 to 6000. The lambda values increased exponentially in this range. The results are summarized in the graphs below:

Error plot for different lambda values for model trained with 49 features with genre information

Error plot over 20 epochs for model with 30 hidden features with no genre information

Error plot over 20 epochs for model with 30 hidden features and no genre information

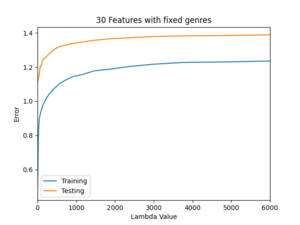
From the graphs, it is evident that all three models had similar performance. For all three models, their testing error was between 1.1 and 1.4 while their training error was much lower. The training error being much lower than the testing error was consistent across all lambda values.

The following table summarizes the best results of each of the three models. Error is measured with average sum of squares:

Table 1: Summary of Best Model Training Error and Testing Error

Training Data	Lambda Value	Training Error	Testing Error
Baseline: Predicting mean rating		1.26	1.39
Model 1: 30 hidden features trained on ratings	3.305	0.653	1.103
Model 2: 49 hidden features trained on ratings and genres	17.062	0.715	1.112
Model 3: 30 hidden features trained on ratings and genres	13.496	0.667	1.107

Performance between models was very similar. The model with the best testing performance was model 1 which was trained on user ratings and had 30 hidden features. The model with the best training performance was the third model which was trained on user ratings and genres with 30 hidden features.

Conclusion

I hypothesized that the model wth the best performance would be the model with the most hidden features. This was not true. The best model was the model trained on ratings. All three of my models suffered from overfitting and despite efforts to mitigate it through lowering the number of epochs and increasing regularization, the models still overfit.

There are many ways to perform collaborative filtering, some of which have been researched on other wiki pages (see related pages section). Future work could look to implement some of the other methods that have been use for collaborative filtering. Matrix factorization is one of the simpler methods, which could be a reason for poor model performance.

To Add

Put links and content here to be added. This does not need to be organized, and will not be graded as part of the page. If you find something that might be useful for a page, feel free to put it here.