By the Taylor series expansion,

If we isolate  in the above, we get that
in the above, we get that

Similarly, by Taylor series expansion, we have

and

If we add the two equations above together, we get that

If we isolate  in the above, we get that
in the above, we get that

From these, we see that we can approximate  by
by

and  by
by

Hence, we can approximate the equation

by

If we isolate  in the above, we get that
in the above, we get that
![{\displaystyle u(x,t+\Delta t)=u(x,t)+{\frac {\Delta t}{(\Delta x)^{2}}}[u(x+\Delta x,t)-2u(x,t)+u(x-\Delta x,t)]+t\Delta t.\;\;\;{\text{(1)}}}](https://wiki.ubc.ca/api/rest_v1/media/math/render/svg/8c75fd391a8927a0e94e169e15e18b8306b4411f)
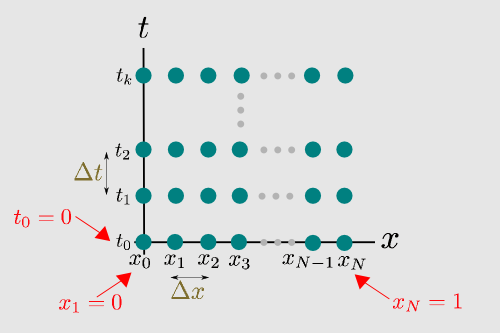
Next we will put  mesh points in the interval
mesh points in the interval ![{\displaystyle [0,1]}](https://wiki.ubc.ca/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d) . Let
. Let

where

Here,  and
and  . Similarly, we will let the mesh points in
. Similarly, we will let the mesh points in  be
be

for some small time step  .
.
At  and
and  , equation (1) becomes
, equation (1) becomes
![{\displaystyle u(x_{n},t_{k+1})=u(x_{n},t_{k})+{\frac {\Delta t}{(\Delta x)^{2}}}[u(x_{n+1},t_{k})-2u(x_{n},t_{k})+u(x_{n-1},t_{k})]+t_{k}\Delta t.}](https://wiki.ubc.ca/api/rest_v1/media/math/render/svg/53dbde6f87e3d2f68d9bdd15c0c0e6395a3622aa)
To get the above, we used
 .
.
Using the notation  , we can write the above as
, we can write the above as
![{\displaystyle u_{n}^{k+1}=u_{n}^{k}+{\frac {\Delta t}{(\Delta x)^{2}}}[u_{n+1}^{k}-2u_{n}^{k}+u_{n-1}^{k}]+t_{k}\Delta t.\;\;(2)}](https://wiki.ubc.ca/api/rest_v1/media/math/render/svg/dd1aa4f97022267fcf44b51cd417688ca01c00de)
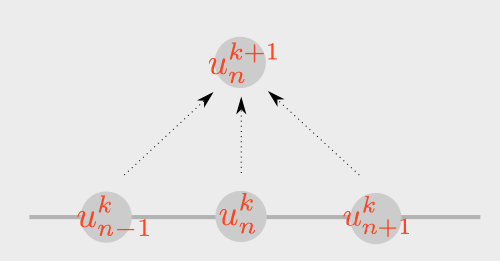
If we look at the above equation, we see that for each fixed  , it gives us a scheme to compute
, it gives us a scheme to compute  once
once  is known for
is known for  .
.
For the initial condition  , we set
, we set

For the boundary condition  , we set
, we set

Now, for the boundary condition  , there is more than one way to handle that. One possible way is to set
, there is more than one way to handle that. One possible way is to set

which implies

If we allow an extra mesh point to the left of  , the above gives
, the above gives

Hence, for  , equation (2) can be rewritten as
, equation (2) can be rewritten as
![{\displaystyle {\begin{aligned}u_{0}^{k+1}&=u_{0}^{k}+{\frac {\Delta t}{(\Delta x)^{2}}}[u_{1}^{k}-2u_{0}^{k}+u_{-1}^{k}]+t_{k}\Delta t\\&=u_{0}^{k}+{\frac {\Delta t}{(\Delta x)^{2}}}[u_{1}^{k}-u_{0}^{k}]+t_{k}\Delta t.\end{aligned}}}](https://wiki.ubc.ca/api/rest_v1/media/math/render/svg/3315244d3c0afaaf645ffcc6bbeb35af5f3c7559)
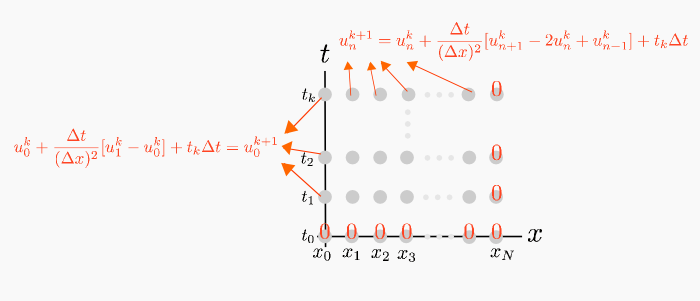
Referring to the diagram above, to find an approximate solution to this problem, we first set the initial conditions

and the boundary condition

Then, we compute  from
from  by
by
![{\displaystyle u_{0}^{1}=u_{0}^{0}+{\frac {\Delta t}{(\Delta x)^{2}}}[u_{1}^{0}-u_{0}^{0}]+t_{0}\Delta t}](https://wiki.ubc.ca/api/rest_v1/media/math/render/svg/a9e941555ab0cbc32127b1b5c6bc05ba872d3bad)
and
![{\displaystyle u_{n}^{1}=u_{n}^{0}+{\frac {\Delta t}{(\Delta x)^{2}}}[u_{n+1}^{0}-2u_{n}^{0}+u_{n-1}^{0}]+t_{0}\Delta t\;\;{\text{for}}\;\;n=1,2,3,\cdots ,N.}](https://wiki.ubc.ca/api/rest_v1/media/math/render/svg/721ac50d34eface326914547337f4f1e46afb1ac)
Once we have  , we can iterate the process to find
, we can iterate the process to find 













![{\displaystyle u(x,t+\Delta t)=u(x,t)+{\frac {\Delta t}{(\Delta x)^{2}}}[u(x+\Delta x,t)-2u(x,t)+u(x-\Delta x,t)]+t\Delta t.\;\;\;{\text{(1)}}}](https://wiki.ubc.ca/api/rest_v1/media/math/render/svg/8c75fd391a8927a0e94e169e15e18b8306b4411f)

![{\displaystyle [0,1]}](https://wiki.ubc.ca/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)









![{\displaystyle u(x_{n},t_{k+1})=u(x_{n},t_{k})+{\frac {\Delta t}{(\Delta x)^{2}}}[u(x_{n+1},t_{k})-2u(x_{n},t_{k})+u(x_{n-1},t_{k})]+t_{k}\Delta t.}](https://wiki.ubc.ca/api/rest_v1/media/math/render/svg/53dbde6f87e3d2f68d9bdd15c0c0e6395a3622aa)


![{\displaystyle u_{n}^{k+1}=u_{n}^{k}+{\frac {\Delta t}{(\Delta x)^{2}}}[u_{n+1}^{k}-2u_{n}^{k}+u_{n-1}^{k}]+t_{k}\Delta t.\;\;(2)}](https://wiki.ubc.ca/api/rest_v1/media/math/render/svg/dd1aa4f97022267fcf44b51cd417688ca01c00de)














![{\displaystyle {\begin{aligned}u_{0}^{k+1}&=u_{0}^{k}+{\frac {\Delta t}{(\Delta x)^{2}}}[u_{1}^{k}-2u_{0}^{k}+u_{-1}^{k}]+t_{k}\Delta t\\&=u_{0}^{k}+{\frac {\Delta t}{(\Delta x)^{2}}}[u_{1}^{k}-u_{0}^{k}]+t_{k}\Delta t.\end{aligned}}}](https://wiki.ubc.ca/api/rest_v1/media/math/render/svg/3315244d3c0afaaf645ffcc6bbeb35af5f3c7559)




![{\displaystyle u_{0}^{1}=u_{0}^{0}+{\frac {\Delta t}{(\Delta x)^{2}}}[u_{1}^{0}-u_{0}^{0}]+t_{0}\Delta t}](https://wiki.ubc.ca/api/rest_v1/media/math/render/svg/a9e941555ab0cbc32127b1b5c6bc05ba872d3bad)
![{\displaystyle u_{n}^{1}=u_{n}^{0}+{\frac {\Delta t}{(\Delta x)^{2}}}[u_{n+1}^{0}-2u_{n}^{0}+u_{n-1}^{0}]+t_{0}\Delta t\;\;{\text{for}}\;\;n=1,2,3,\cdots ,N.}](https://wiki.ubc.ca/api/rest_v1/media/math/render/svg/721ac50d34eface326914547337f4f1e46afb1ac)
