PHYS341/2023/Project4

How the Pitch of a Guitar is Affected by Tensile Properties in its Strings

By: Auliver Liu and Oliver Evans

Introduction

Guitars are a staple to the music world, being one of the most recognizable and renowned instruments. While many people play the guitar, not many understand the physics behind its sound formation. Making a guitar is a fascinating process that involves carefully selecting materials and tuning each individual string to achieve the perfect sound. By understanding how different materials of the body and properties of strings impact the pitch, you can create a unique and personalized guitar that delivers an unparalleled musical experience. This report will be an investigation into the necessary principles required to understand how pitch can vary depending on a string’s tensile properties and the body’s structure anatomy. Explicitly, this will be achieved through the construction of a home-made guitar, comprising of 4 strings each of different properties to demonstrate how tensile properties affect pitch.

History of the Guitar

Baroque Guitar

It is unknown as to when the first guitar was created, but the term has been used loosely throughout history, describing any instrument with a neck, flat wooden soundboard, ribs and a flat back. The oldest recorded evidence is a 3,300-year-old stone carving of a bard playing a stringed instrument representative of a guitar. As time progressed, Spain began to use guitars more frequently. It started off with chordophones which were classified as guitars at the time, which eventually evolved into a five stringed baroque guitar. Around 1850, the modern-day guitar was founded, developed by numerous Spanish inventors and this is the model we use today for acoustic guitars. Evolution continued with the creation of electric guitars which use electromagnetic pickups or a converter that transforms the vibration of strings into electric signals that are sent to an amplifier through cables or radio transmitters.

How does a Guitar Work?

A regular acoustic guitar normally has 6 strings, each tuned to a different note. These strings are connected to the neck via tuning pegs which allow the user to fine-tune the pitch. The strings are then attached to the bridge towards the base of the guitar. The strings pass over an opening in the body, which allow the sound vibrations to resonate and amplify the sound produced.

There are different variations of guitars such as acoustic and electric with different numbers of strings. They all mostly function the same, however some aspects perform differently, such as an electric guitar digitally amplifying the strings' vibrations as opposed to resonating in the body for acoustic guitars. In this project, we will be recreating an acoustic guitar.

When a string is plucked, it oscillates in periodic motion which moves the air molecules around it to vibrate in the same frequency of thee string and produces longitudinal waves in the air. Conversely, the wave formed in a guitar string is a transverse wave from the side-to-side motion and it is a standing wave because the waves bounce off the ends of the string. Sound is then produced through vibrations which propagate through the air via longitudinal waves. Different properties of the source of the vibration will cause different timbre, pitch and volume. Using our home-made guitar, we will be investigating what properties affect a guitar’s pitch: key factors are the mass, tension, and length of the strings. It is known that according to Hooke’s Law, there is a relationship for force given by $F=-kx$ where $k$ is a constant dependent on a material’s elasticity, and $x$ is the displacement from the equilibrium. From Newton’s Second Law ($F=ma$), we know that acceleration is directly affected by the amount of force (assuming mass is constant), and hence the velocity of the propagated waves will also increase (as can be concluded from the equation $v=u+at$, where velocity is proportional to acceleration). By $f=\upsilon /\lambda$, these changes in velocity will lead to different frequencies of sound to be produced; notably, higher tension will cause higher frequencies. Since $\lambda$ is directly proportional to $L$ (length of string) for all harmonics (f, 2f, 3f, etc.), longer strings will produce lower frequencies due to having longer wavelengths. For mass, given the derived formula for period for oscillations abiding Hooke's Law, $T=2\pi {\sqrt {m/k}}$, we find that larger mass causes lower frequencies, and smaller $k$ or string elasticity causes higher frequencies due to the $f=1/T$ relationship. Additionally, pressing down on the frets or anywhere along the neck will limit the length of string that is free to oscillate which causes higher pitches the closer the fret is to the guitar sound hole because of the shorter string length and shorter resulting wavelength.

Designing the Guitar

Figure 1. Initial Design for Guitar

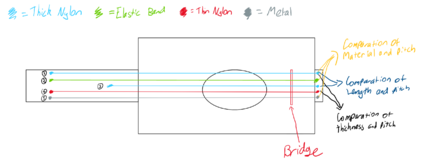
Initial planning stages for the guitar was to have 5 strings across a body (shoe box and neck) made of cardboard. Comparisons were made by testing the different frequencies that resulted from different materials such as nylon, rubber and metal, as well as contrasting the tones that are produced from different string lengths. However, we do not possess the technology to accurately measure and keep the tension force of strings constant which makes comparisons between a full length versus half length nylon string difficult. Thus, we decided upon installing a tuning mechanism such as a screw to tie the strings on which would be better suited on wooden body due to the higher density and thickness.

Figure 2. Guitar - Front View

There are also several differences between using cardboard versus wood:

In terms of sound quality, wood guitars tend to produce a richer, more full-bodied sound and rich spectrum of harmonic partials than cardboard guitars. This is because wood is a more resonant material, which means that it vibrates more easily and produces a more natural tone. Cardboard guitars, on the other hand, tend to have a more muted, flat sound. As sound waves reflect off hard surfaces which create reverberation or echo effects, wood is a superior material.

Regarding durability, wood guitars are generally more sturdy and long-lasting than cardboard guitars. While cardboard guitars can be lightweight and easy to transport, they are more prone to damage from moisture, heat, or pressure. Wood guitars are much more resistant to tough environmental conditions and can last for decades if maintained.

As the actual air displaced by a vibrating string is minimal, it must be transmitted to the body through a bridge. The larger surface area vibrations create higher amplitudes by moving more air at the body's resonant frequencies. Explicitly, the body does not amplify all frequencies of the string, but only some frequencies have higher resonances with the wood body which gives different timbres.

For our guitar, we made a triangular shape to save costs and materials. We cut three pieces of dark brown oak wood to create the sides of the triangle, and oak wood for the base and top layer which includes the neck. The total dimensions standing upright are a height of 53.8 cm, length/side of 17.5 cm and a width/front base of 21.5 cm.

Maple wood was chosen due to it offering higher resonant frequency or higher treble compared to other tonewoods, sounding crispier, more dense, adds more volume, and gives the guitar an athletically pleasing look. Conjunctively, white oak wood was chosen due to it having properties of a sustaining tone with a warm yet strong lower frequencies and it was cheap to acquire. Thus, oak gives the guitar a balanced sound of resonating frequencies combined with maple. It is important to note that oak is very porous and prone to crack during construction as shown by the guitar having an empty hole in Figure 2 on the bottom left.

Figure 4. Strings and Bridge

Figure 3. Guitar - Side View

Our final decisions for the strings were to have one 50 cm nylon string (green), one 50 cm rubber string (gold), one 50 cm 24-gauge galvanized steel wire, one 25 cm nylon string (white). The strings are tied to a nail at the bottom and to a screw-in hook at the top fastened to a nut, allowing for approximately equal lengths of string. The screw in hook allows for adjustments in tuning the string's pitch. The bridge was made of dark oak wood and was nailed and glued on. Connections between the pieces of wood were glued on the inside to prevent sound from escaping the guitar from areas besides the sound hole.

Tuning the Guitar

Figure 5. Strings Tied on Hook Screws

In order to change the frequency of the strings, we must increase the tension of the strings and make audible sounds. This is done by tightening or loosening the hooks which wraps or unwraps the strings around the hook.

Methodology and Expected Physics

The experiment conducted on the home-made guitar will allow us to investigate how $k$ or elasticity, mass, and length can be adjusted to affect the pitch and timbre of the sound produced by a guitar string.

The guitar will have 4 strings, String 1 being composed of nylon, String 2 composed of steel and String 3 composed of the same nylon as String 1 but half the length. String 4 will be made of rubber.

Effects of Material Type

String 1, String 2 and String 4 will be compared with each other to demonstrate how materials can affect the pitch and timbre.

Guitars often use either steel or nylon strings. While an untrained person may not recognize the audio difference between the two, experienced musicians have preferences due to the sound that is produced by strings of different materials. While the strings are tuned to the same notes, the amount of tension needed to tune a nylon string is more than that of a metal string. Alternatively, steel has a larger mass than nylon and rubber which may contribute to a lower frequency, but it also is a stiffer material which may contribute to a higher frequency. For rubber, more elastic materials are expected to produce lower frequencies. These inconsistencies will be investigated in our report by maintaining the same tension in the strings and analyzing the differences in frequency distributions between the 3 strings.

Figure 6: Trigger-Style Capo.

Effects of String Length

String 1 and String 3 will then be compared, to demonstrate how a change in length can also affect the resulting sound generated.

Guitars always have strings of the same length, however when pressing a finger on a string or placing a "capo" (see Figure 6) on a fret, the length of the string changes and hence so will the sound. This is due to the phenomenon of shorter strings will vibrating at a higher frequency than longer strings, assuming the applied force and tension is the same.

Note that the amount of force put onto each string may vary, resulting in different amplitudes for each comparison.

Quantitative results will be recorded and analyzed using the software Audacity.

Hypothesis

For varied material types, it is expected that materials with a higher elasticity and greater mass will result in a frequency distribution where lower frequencies are more prevalent. Hence in the case of the homemade guitar, created for this investigation, String 2 (steel) will have the higher mass and hence a lower pitch and frequency spectrum with frequencies 400Hz and below more prevalent; notably, since the steel is a 24 gauge, it is quite elastic compared to other metals. String 4 (rubber) will have a lower frequency than String 1 (nylon) and String 2 (steel) as rubber will have more elasticity and hence a slower vibration. We hypothesize that there will be frequencies below 300 Hz to be more established.

In the case of string length, we expect a shorter string to have a higher pitch. Hence for the case of this experiment, String 3 will have a higher pitch than String 1, with frequencies of 600Hz and higher are more distinct in its spectra.

Results

Figure 7 is the frequency distribution of String 1 and will be compared to the other strings. See Audio 1 for a recording of String 1. The note we hear is closest to a B₃ note with a frequency of approximately 245 Hz.

Figure 7: Frequency Distribution of String 1

Audio 1: Full length nylon string (String 1)

Figure 8 has a spectrum with the lower frequencies being louder than the higher frequencies. This means that the pitch of the steel is lower than that of String 1, as the frequencies of 10000 Hz and above are less prevalent. See Audio 2 for a recording. The audible tone we hear is D₃ which is about 148 Hz, steel has the longest resonance and sustained tone compared to the other strings.

Figure 8: Frequency Distribution of String 2

Audio 2: Steel String (String 2)

Figure 9 has larger spectra at 10000 Hz and higher frequencies, resulting in a higher pitch than String 1. See Audio 3 for a recording. The note we hear is an F#₄ which is approximately 360 Hz.

Figure 9: Frequency Distribution of String 3

Audio 3: Half length nylon string (String 3)

Figure 10 represents the spectra of String 4. While there are more high frequency spectra present than String 1, the lower frequencies of around 100 Hz are larger in amplitude. This resulted in a lower pitch compared to String 1 and String 3. See Audio 4 for a recording. The note that we hear is a G#₂ which is about 104 Hz, this string resonates longer than the nylon strings, but less than the steel string.

Figure 10. Frequency Distribution of String 4

Audio 4: Rubber string (String 4)

Discussion

When considering our hypotheses, our qualitative estimates were almost correct, however our quantitative ones were not close enough to be able to say they were conclusive. With regards to our observations with string length and pitch, we were correct in hypothesizing that String 3 (half-length nylon) would have the higher pitch over String 1 (nylon). What was unexpected, was the difference in frequency distributions being significantly higher than 600 Hz. The frequency spectra of String 3 were mainly 1000 Hz and above as opposed to our estimated 600 Hz.

With our experiment with string material and pitch, our hypotheses were also slightly incorrect. It was expected that, from lowest pitch to highest, the order would be String 4 (rubber), String 2 (metal) then String 1 (nylon), and this was consistent with our results. However, our estimates for the frequencies were also incorrect. While it was expected for String 2 to have more prevalent spectra below 400 Hz, it was found that the threshold was 300 Hz instead. This was similar with String 4, except frequencies around 100 Hz were also well established and high in amplitude.

Explicitly, String 1 and String 3, holding tension force equal, halving the string length would double the frequency under $f=\upsilon /\lambda$ since $\lambda$ is directly proportional to $L$, but due to measurement errors and inaccurate tension adjustments, we only saw a difference of frequencies from 245 Hz to 360 Hz. Conversely, this is sufficient to conclude that designing shorter strings on a guitar increase the frequency and pitch of that string. Comparing String 1 (nylon, 245 Hz) to String 2 (steel), we find that the steel string has a much longer sustained tone while the nylon string's sound rapidly decays. This is due to the steel string having a larger mass and is more dense compared to nylon and produces a lower frequency of 148 Hz; furthermore, greater masses can move more air molecules which enables the steel string to produce larger amplitudes of sound (Figure 8) compared to the other strings. Note that comparisons of the elasticity of metal is difficult as we do not possess the technology to quantify it. Moreover, String 4 (rubber) produces the lowest frequency of 104 Hz due to it being the most elastic material. Under simple harmonic motion abiding Hooke's Law, we have $T=2\pi {\sqrt {m/k}}$, and due to the high elasticity of rubber or a high $k$ value, the rubber string will have a very low frequency under $f=1/T$ which aligns with our initial assumptions. Rubber also produces a longer sustained tone than the nylon as it has more mass, but less than the steel as it has less mass. Intriguingly, rubber has almost no overtones beyond 3000 Hz compared to the other strings, giving it a unique timbre suitable for bass strings.

Sources of Error

There are some limitations with the experiment performed. A large factor into what could change the results would be the tension in each string. As we constructed the guitar by hand and did not tune it properly, the tension in each string may vary slightly despite our best efforts to make it consistent. Having a higher tension has a direct correlation with pitch, and the result would have a higher pitch. The wave speed may also have a great impact on the frequency as it is calculated by $v={\sqrt {T/\mu }}$, where $T$ is the string tension and $\mu$ mass per unit length of the string. In addition, the thinner the string, the faster the wave speed, which results in higher frequencies, but the wave travels slower as density of the material decreases. Another source of error may be the amount of plastic deformation the strings undergo. As we used materials found around a regular household, the steel string could bend slightly and give frequency distributions and sound waves that are irregular and are not expected. This would most likely prove to be a minimal error as the guitar did not undergo heavy use and was used fairly briefly.

If this experiment were to be performed again, having better tuning pegs and a device to measure tension would be ideal, as this would allow the strings to have an equal amount of tension as well as having the ability to regulate it. This would also allow for a study into tension and pitch to be performed. For validity, Having a fixed tension across the strings will also allow for less variances in error and create accurate results. The reliability of the experiment could also be improved but taking numerous recordings of the strings and comparing the differences, however this would need to be carefully observed due to plastic deformation in the strings.

Conclusion and Demo

While the creation of the guitar was well executed, with more time and advanced technology, improvements could have been made to ensure the strings provide good results. One of these improvements would be to use strings with a stronger material which is more durable. This would allow for tests to be repeated and for demonstrations to be performed. Another improvement could be the shape of the body and utility of the bridge. While our guitar had these features present, using them more efficiently could provide a louder sound and make it more usable. Additionally, we could explore adding a thick or light coating of paint on the body which may change the tone and sustain of the sounds or try sanding the wood which may improve tone and resonance for high-density woods like maple. However, our guitar produced sound which was acceptable so this feature would be more for quality of life and aesthetics over anything else.

The homemade guitar performed successfully and provided a deeper understanding as to why the pitch of a note played on a guitar can change. Our results showed that the material and length of strings have a great effect on the pitch and why many guitar enthusiasts may decide on various body and string materials to showcase different tones and timbres aligning with their artistic expressions.

Homemade Guitar

Here is a short demonstration of playing the guitar, this is the theme from Mary Had a Little Lamb: