Simple and Damped Harmonic Motion

This article is part of the PhysicsHelp Tutoring Wiki

Simple Harmonic Motion

Many simple systems can be approximated or even accurately described by Simple Harmonic Motion. The motion of a pendulum or spring, of waves on the ocean or waves of sound all have similar traits.

Simple harmonic motion refers to motion that can be modeled by the following equation:

$x=A\cos(\omega t+\phi )~$

which solves the differential equation:

$F=m{\frac {d^{2}x}{dt^{2}}}=-kx$

$x$ is the position in metres ($m$).

$k$ is a constant of proportionality, normally called the spring constant, in kilograms per second squared ($kg/s^{2}$).

$A$ is the amplitude in metres ($m$).

$\omega$ is the angular frequency in radians per second ($s^{-1}$).

$t$ is the time in seconds ($s$).

$\phi ~$ is a constant phase shift in radians.

One can show, by differentiating the first equation twice, that $\omega ={\sqrt {\frac {k}{m}}}$.

Note that although $\omega$ is written in radians per second, radians have no physical units, and so $\omega$ just has units of $s^{-1}$. The if one wants to talk about the revolutions or rotations per second of an oscillation, we usually write $f$ and note that since there are $2\pi$ radians in one full rotation,

$f={\frac {\omega }{2\pi }}$

This frequence $f$ also has units of $s^{-1}$, but in this case we call them Hertz, and denote $Hz$.

Physically, the simple harmonic oscillator represents an object, such as a mass on a spring, moving back and forth from a minimum to a maximum position with neglegible resistance. The minimum and maximum positions correspond to $-A$ and $A$ in the first equation. We can talk about the period of the system, meaning the time it takes an object to start from $A$, move to $-A$ and then get back to $A$ again. We usually denote the period $T$ and it is clear from the definitions that:

$T={\frac {1}{f}}={\frac {2\pi }{\omega }}$

The constant $\phi ~$ in our first equation represents the initial state of the system. Given any particular initial position and velocity, we can determine a $\phi$ that will match the objects motion for all $t$. We can see from elementary triginometry that the first equation can be re-written:

$x=A\sin(\omega t+\phi _{2})~$

Where we have simply $\phi _{2}=\phi +{\frac {\pi }{2}}$.

We can take the derivative of the first expression to find the velocity of the object as a function of time:

$v={\frac {dx}{dt}}=-\omega A\sin(\omega t+\phi )$

One thing to note about these expressions for position and velocity is that when the position is equal to zero, which occurs whenever $\omega t+\phi ={\frac {n\pi }{2}}$, where $n$ is any integer, the velocity is at a maximum magnitude, either $A\omega$ or $-A\omega$. This means that the object is moving faster when it is close to the middle of its motion. Correspondingly, when the position is at a maximum or minimum ($\pm A$), which occurs whenever $\omega t+\phi =n\pi ~$, where $n$ is any integer, the velocity is at a minimum magnitude, $0$. Thus the object stops instantaneously as it reaches its maximum and minimum positions.

Calculating Energy

Calculating energy in a simple harmonic spring or pendulum is similar to other energy calculations. Most importantly, the law of conservation of energy is the key to solving such problems.

In the case of an oscillating spring, the maximum energy can be calculated using 1/2 kA^2 (at the point where Amplitude is maximum). This represents the points at which the spring has become deformed (either stretched or compressed) and is storing energy (remember 1/2 kx^2 is energy in a spring and A is the maximum displacement). Alternatively, we can use the maximum velocity (the velocity with the displacement from the equilibrium position is 0) and state that total energy is 1/2mv^2. At times, we need to combine both equations to solve points which are not at maximum amplitude or maximum velocity (i.e. Total Energy = 1/2 kA^2 + 1/2mv^2 for some values of A and v which are not maximum). When you are not given k and/or m, it is still possible to find max amplitude using max velocity and omega!

Calculating phi

Many people often have trouble calculating $\phi$. Let's assume we have a problem where we have already calculated or were given $A$ and $\omega$. Most problems will tell you, in some way or another, the amplitude at a time $t$. For instance, one might say that the object is released at some maximum amplitude $A$ at time $t=0$. This is a very simple case. We can see immediately from the first equation that if $t=0$ then $A\cos(\phi )=A~$ and so $\phi =0~$ is the solution. It turns out that $\phi =2\pi ~$ will also work, and in general if you add any multiple of $2\pi$ to $\phi ~$ you will still have a valid answer. By convention, we usually like to talk about the solutions that is somewhere between $0$ and $2\pi$.

One of the most important steps is to identify which function you will be using (i.e. cosine or sine). Drawing out a regular sine or cosine function (and/or a unit circle) can help you estimate what value and what direction the shift needs to be. The drawback with this method is that it is important to be able to draw or derive a snapshot graph for x=0 and t=0 (as well as knowing the direction of the wave). While limited, it can be a powerful indicator of whether or not the actual data supports your answer. Remembering that half a wavelength is equal to pi radians, it is possible to make all answers somewhere between negative and positive pi.

In the more general case, a problem will tell you that at some time $t=t_{1}$, the object is at position of $x_{1}$ or has a velocity $v_{1}$. Here we have to be more careful to find the correct answer. The best approach is to just do lots of examples to get used to the ideas.

Q: Consider a mass on a spring with amplitude $3cm$ and frequency $2\pi$ radians per second. If you know that at time $t=0.5s$ the position is $-3/{\sqrt {2}}cm$, and that the object is moving downwards, then what is $\phi ~$?

A: Look at a graph of the objects position and over time.

A graph of two possible equations with amplitude -3/sqrt(2) at t=0.5; note that the derivatives of each curve differ in sign.

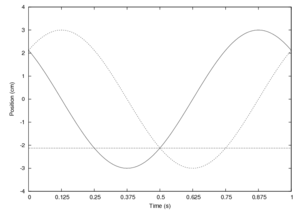
The dashed line is at $x=-3/{\sqrt {2}}$. Note that given any solution $\phi _{0}~$ (corresponding to the solid curve), we can find another solution $\phi _{1}~$ (corresponding to the dotted curve), which passes through the same point at the same time. Since both of these curves pass through the correct point at the correct time, we have to be able to tell them apart. Luckiliy, by some handy properties of triginomotry, the velocity in each of these solutions will always differ in sign, so it is enough to know which direction the object is travelling in to find the correct answer. Thus we can solve our first equation for $\phi ~$:

$\phi =\cos ^{-1}({\frac {x}{A}})-\omega t=\cos ^{-1}(-{\frac {1}{\sqrt {2}}})-\pi =-{\frac {\pi }{4}}$

Plug this into the equation for the velocity, and we get:

$v=-\omega A\sin(\omega t+\phi )=-2\pi (3)\sin(\pi -{\frac {\pi }{4}})={\frac {1}{\sqrt {2}}}cm/s$

But this velocity is positive, and we were told that the object is travelling downwards. We need to find the other solution of $cos^{-1}$ (remember that it is a multi-valued function) that is within the same period. You may remember from high school trigonometry that we can get another solution to cosine by subtracting the first solution from $2\pi$ and solving for $\phi _{2}~$.

$\omega t+\phi _{2}=2\pi -(\omega t+\phi )~$

$\phi _{2}=2\pi -2\omega t-\phi ={\frac {\pi }{4}}$

Plugging this into our equation for velocity as above gives us a result of $-{\frac {1}{\sqrt {2}}}cm/s$, which works. Thus our answer is $\phi ={\frac {\pi }{4}}$

A very similar type of problem is one where the velocity is specified instead of the position. In this case the problem is solved in the exact same way: We solve the velocity equation to find an initial answer for $\phi ~$ and check if that corresponds with what we know about the position. If not, we must find another solution to sine, which, again from high school trigonometry, is $\pi$ minus the first solutions. Hence:

$\omega t+\phi _{2}=\pi -(\omega t+\phi )~$

$\phi _{2}=\pi -2\omega -\phi ~$

Damped Harmonic Motion

In real systems, masses on springs don't continue to oscillate forever at the same amplitude; eventually the oscillations die away and the object stops. This is due to the fact that springs are not very efficient at storing and releasing energy. Much of the energy is disappated as heat due to friction within the spring. In order to better model these kinds of systems we can talk about the damped harmonic oscillator, which is the soltion to the differential equation:

$F=m{\frac {d^{2}x}{dt^{2}}}=-kx-b{\frac {dx}{dt}}$

Where we have taken the diffential equation for the simple harmonic oscillator and added a damping term, $-b{\frac {dx}{dt}}$, where $b$ is called the damping constant or drag coefficient. Since this damping term acts in the opposite direction of motion and is proportional to velocity, it causes objects with high vlocity to slow down quickly. We can solve the damped harmonic oscillator equation by using techniques that you will learn if you take a differential equaitons course. The solutions are of the form:

$x=Ae^{-{\frac {b}{2m}}t}cos(\omega t+\phi )$

where $\omega ={\sqrt {\omega _{0}^{2}-{\frac {b^{2}}{4m^{2}}}}}$

and $\omega _{0}={\sqrt {k/m}}$

Observe that $\omega _{0}$ is just the frequency of oscillation of a simple harmonic oscillator. Thus we can see that if we add damping to a simple harmonic oscillator, the frequency will change and the amplitude of the oscillations will exponentially decay with time.

Forced / Driven Oscillations

For forced oscillations (also known as driven oscillations) you cannot usually solve the position of the oscillator as a function of time except in steady state without using more advanced techniques with differential equations. What this means is that usually the solution for a given set of initial conditions of a damped oscillator has a complicated intial behaviour, called transients, which are quickly damped away as the system approaches what is called the steady state solution, which is the long-term periodic behaviour of the system.

For example, if we were to take a normal damped mass-on-a-spring system and we were to "drive" it by pushing it back and forth continuously at some particular frequency, i.e.

$F=A\cos(\omega t)~$

the solution (the steady state behaviour of the system) would take the form:

$x={\frac {A}{Z_{m}}}\cos(\omega t+\phi )$

$Z_{m}={\sqrt {b^{2}-{\left(\omega m-{\frac {k}{\omega }}\right)}^{2}}}$

$x$ is the displacement in meters ($m$).

$A$ is the amplitude of the driving force, in Newtons ($N$).

$\omega$ is the frequency of the driving oscillations in radians per seconds ($s^{-1}$).

$\phi ~$ is a phase constant in radians.

The most important thing to note from this is that the amplitude is maximum when $Z_{m}$ is a minimum. This occurs when $wm={\frac {k}{\omega }}$ or $\omega ={\sqrt {\frac {k}{m}}}$, that is to say the driving frequency is the same as the natural frequency for a spring system. This idea that maximum amplitude occurs when the system is driven at its natural frequency occurs for all damped driven systems.

Problem Solving

Q On your first trip to Planet X you happen to take along a $200g$ mass, a $40cm$ long spring, a meter stick, and a stopwatch. You're curious about the free-fall acceleration on Planet X, where ordinary tasks seem easier than on earth, but you can't find this information in your Visitor's Guide. One night you suspend the spring from the ceiling in your room and hang the mass from it. You find that the mass stretches the spring by $27.4cm$. You then pull the mass down $10.1cm$ and release it. With the stopwatch you find that 10 oscillations take $17.8s$. Use this information to solve for the acceleration due to gravity, $g$ on Planet X.

A First we use the identity $f={\frac {1}{2\pi }}{\sqrt {\frac {k}{m}}}$ to find the spring constant $k$. $f$ is the oscillations per second, and we know that ten oscillations take $17.8s$, so we can solve

$f={\frac {10}{17.8s}}\approx 0.5617Hz$

and then

$k={(2\pi f)}^{2}m={(2\pi 0.5617)}^{2}(0.200kg)\approx 2.492kg/s^{2}$

We know that when the mass is at rest at $27.4cm$ (or $0.274m$) from its initial equilibrium position, the gravitational force balances out the force of the spring, i.e.

$F=ky=mg$

With $m=200g=0.200kg$, $k=2.492kg/s^{2}$, $y=0.274m$ we can find the gravity g:

$g={\frac {ky}{m}}={\frac {(2.492kg/s^{2})(0.274m)}{(0.200kg)}}\approx 3.414m/s^{2}$

Problem Solving

Q Using a small pendulum of length 0.171 m, a geologist counts 72.0 complete swings in a time of 60.0 s. What is the value of g in this location?

A First calculate the period of the pendulum by dividing the total time by the number of complete swings

T = Time/Number of Oscillations = 60/72 = 0.833s

T = 2(pi)(Root(L/g))

Solve for g = 4 (pi)^2 (L)/ (T^2) = (39.5)(0.171m)/(0.833s)^2 = 9.73 m/s^2

Return to PhysicsHelp