Lecture 10

Faculty of Science; Department of Mathematics
	Course Pages
	Course Policies
	Math Solvers
	Exams
	Quizzes
	Assignments
	Lectures

Readings For This Lecture

Keshet Course Notes:

Chapter 5, pages 90 to 106

Summary

Group 4: Add a summary of the lecture in this space. Include examples, discussion, and links to external sources, if desired.

Exercises

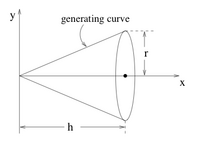
1. Using the diagram below, explain what kind of curve we would use to generate the surface of a cone on its side as a surface of revolution. For a cone of base $r$ and height $h$ , where $h=r$ , find the exact function of the generating curve. Find the volume enclosed by this surface of revolution for $h=1$ .

2. Show that, using the exact same generating curve as in the previous question, the surface of revolution obtained by rotating this curve around the $y$ -axis instead of the $x$ -axis will create a cone with the exact same volume.

3. Find the volume of the “bowl” obtained by rotating the curve $y=4x^{2}$ about the $y$ -axis for $0<x<1$ , using the method of discs.

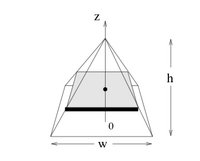
4. Adapt the method of discs to find the volume enclosed by the pyramid given below.

5. Set up the integral that represents the length of the curve $y=sin(x),0<x<2\pi$ .

6. Compute the length of the line $y=2x+1$ in the interval $[-1,1]$ using the arclength formula. Check your work using geometric arguments.

7. A spring has a natural length of 16 cm. When it is stretched $x$ cm beyond that, Hooke’s Law states that the spring pulls back with a restoring force $F=kx$ dyne, where the constant $k$ is called the spring constant, and represents the stiffness of the spring. For the given spring, 8 dyne of force are required to hold it stretched by 2 cm. How much work (dyne-cm) is done in stretching this spring from its natural length to a length 24 cm?

8. Consider a curve $y=f(x)$ over an interval of finite length. Derive a formula for the surface area of the surface of revolution obtained by rotating this curve around the $y$ -axis.