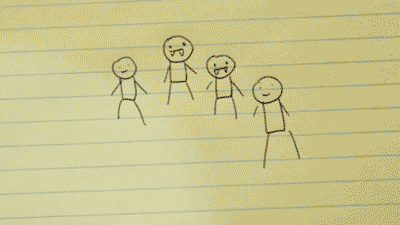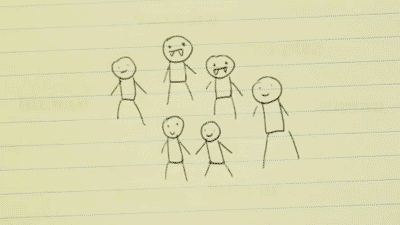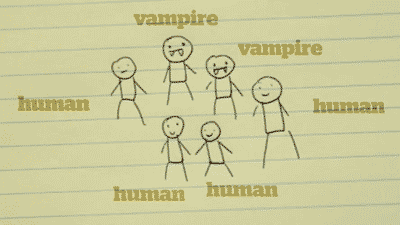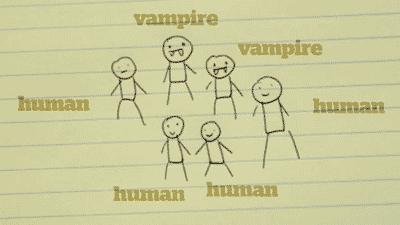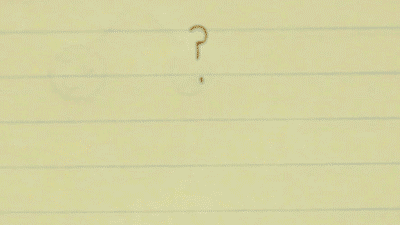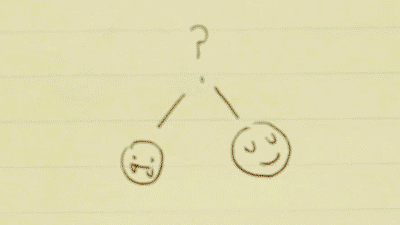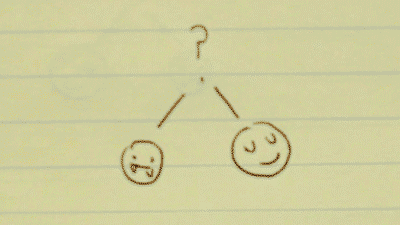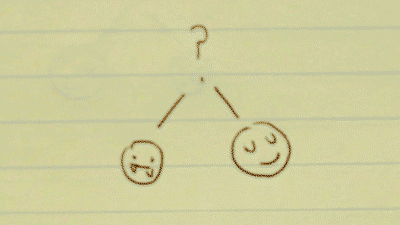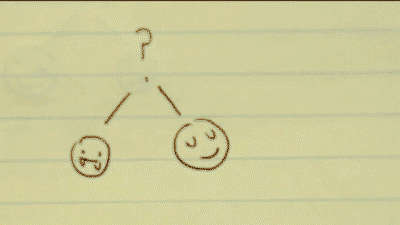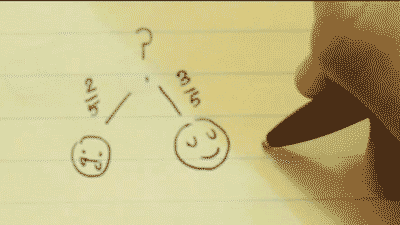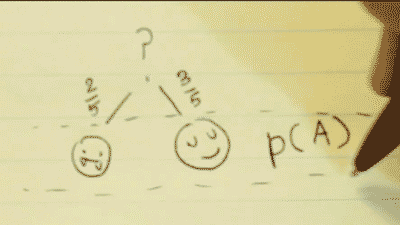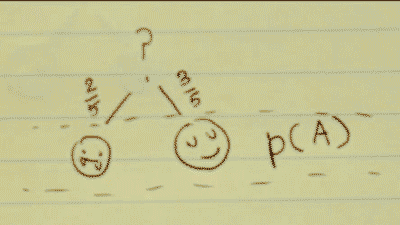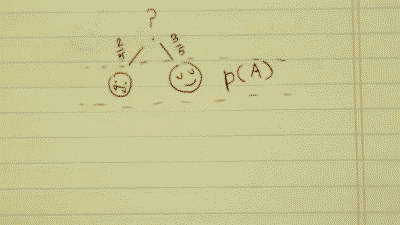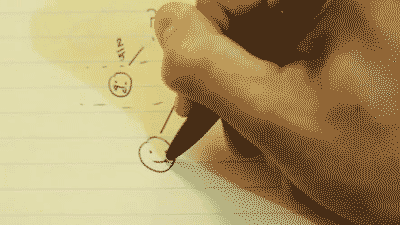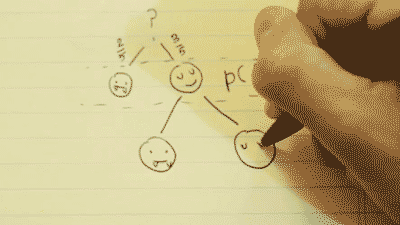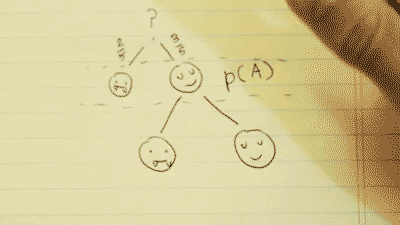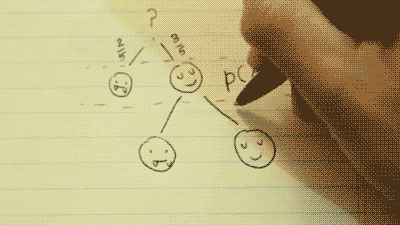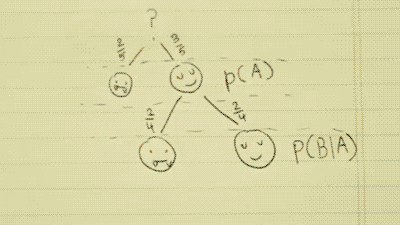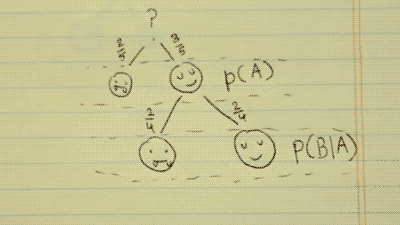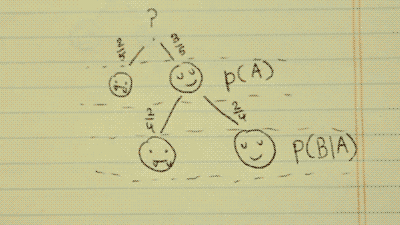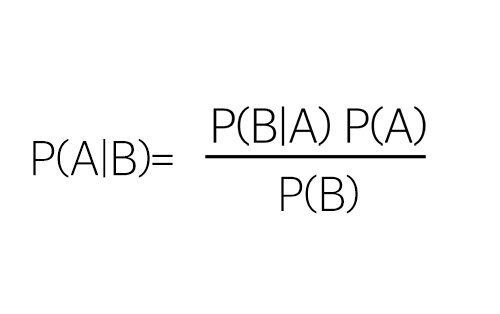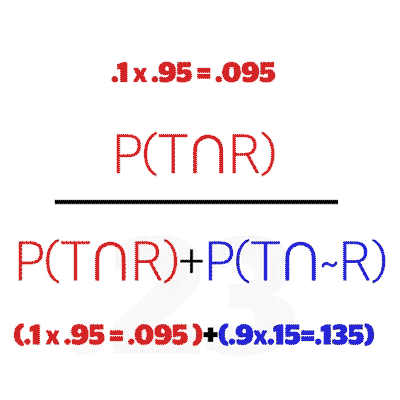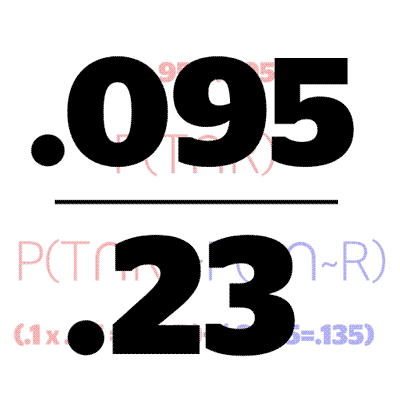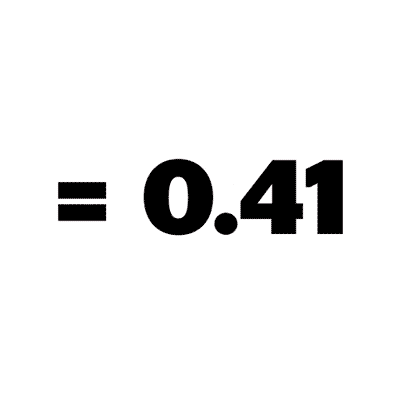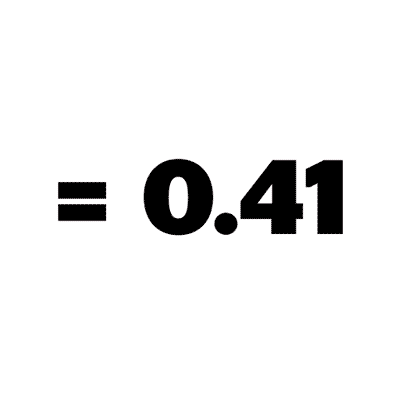This is a page for creating resources for COGS 300 students about probability and causality. Please use an appropriate heading for any material you add.

Section 1: Visualizing conditional probability with trees

Sometimes it can be pretty difficult to understand the probabilistic relationships between variables in Bayes Theorem. Using trees is a handy tool to make conditional probability a bit easier to grasp.

To start off, I'm going to draw a tree diagram for a dependent event, like p(A∩B). Please note that dependent events are a component of Bayesian probability. This is figuring out how to represent the "numerator part" of Bayes Theorem.

Hopefully by the end of this you will understand how p(A∩B) = p(A)*p(B|A)

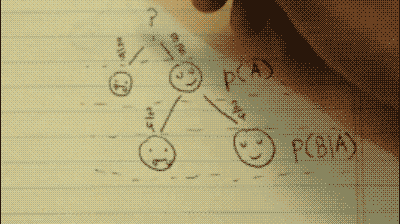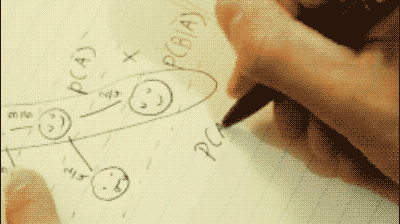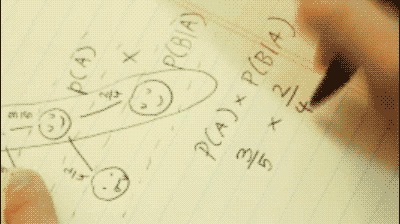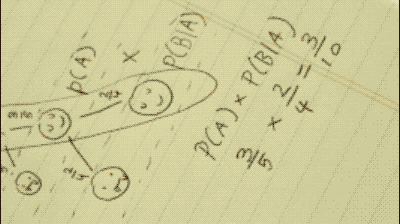
Dependent probability problem

>You have 2 tickets to a Rad All-Night College Party on campus.

>You have 5 possible friends to invite.

>Unknown to you, 2 of your friends are actually vampires. (The other 3 are just normal humans.)

>If you invite a vampire out to the Rad All-Night College Party, they will feast on your blood. If that's not bad enough, you'll die from blood loss, and be enslaved for all eternity as their un-dead servant.

>You select one of your friends to come with you. Then, you select a second.

>What is the probability that you survive the night? (I.e. you pick two humans to come with you.)

written differently: p(A∩B), where A= a human, and B= a human.

To figure this out, all you need to know is the probability of initially picking a human companion (P(A)), and the probability of picking another human, given that your last selection was a human (P(B|A)).

Let's start:

Step 1:

You have two options: pick a vampire, or pick a human.

There is a 2/5 chance to pick a vampire, and a 3/5 chance to pick a human. This can be written as P(A). The probability of A.

Step 2:

Assuming that your last selection was a human, there are now two new possible choices you can make.

This time, the probability of these choices has been changed. There is now a 2/4 chance to pick a vampire, and a 2/4 chance to pick a human. This is because there is one less human to choose from.

This can be written as P(B|A). The probability of B, given A.

Step 3:

Now we must find the probability of both events happening. To do so, we simply multiply our results from step 1 and 2 as so:

P(A)*P(B|A)=P(A∩B)

3/5 * 2/4 = 3/10

Or, if you prefer, in English: [The probability of A] times [the probability of B given A has occurred] is equal to [the probability of B and A]

There is a 30% chance you will survive the Rad All-Night College Party.

Section 2: Applying the tree method to Bayes' theorem

Now that we have a method for visualizing conditional probability, we can start to integrate it into Bayes theorem.

Remember that in section 1 we figured out how to demonstrate the probabilistic relationship between two events (recall that it's written as: P(A)*P(B|A)). This plugs into the numerator of Bayes theorem.

Bayes theorem will help us inductively figure out the probability of event A happening given that event B has occurred.

This is best illustrated with an example:

An application of Bayes theorem

Suppose there was some all-star-varsity-sports league that engaged in some sort of strenuous activity that involved scoring game-points by throwing balls into nets and the like.

Unfortunately, to stay competitive, 10% of players illegally get super jacked on steroids.

As substance abuse has started to become a problem, the Big Sports Federation has decided to administer drug tests to players. They boast that their steroid tests are 95% effective--if an athlete takes their test on steroids, there is a 95% chance the test will detect it.

However, their tests have a 15% chance of giving a false positive.

How accurate is the Big Sports Federation's steroid test? Specifically, what is the probability that an examined athlete has taken steroids given a positive test result?

Written differently, what is P(Player has taken steroids|Positive test result)?

Step 1:

Given the information above, we know the following:

90% of players have not taken steroids.
10% of players have taken steroids.
The test is 95% accurate given the subject has taken steroids.
There is a 15% chance that the test will give a false positive.

This can be formalized as follows:

R = Players who take steroids

T = Test result positive

P(~R)= .9

P(R)= .1

P(T|R)= .95

P(T|~R)= .15

Remember that we want to know P(R|T).

Step 2:

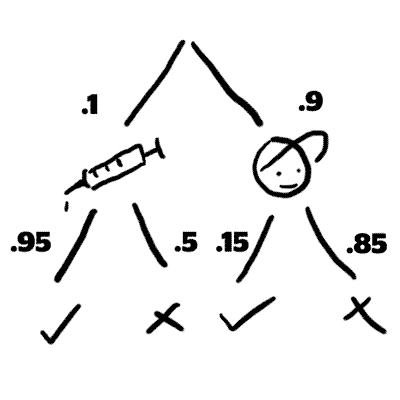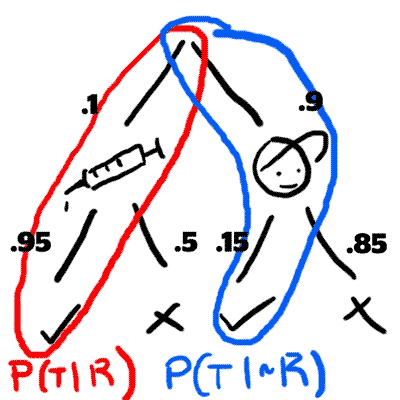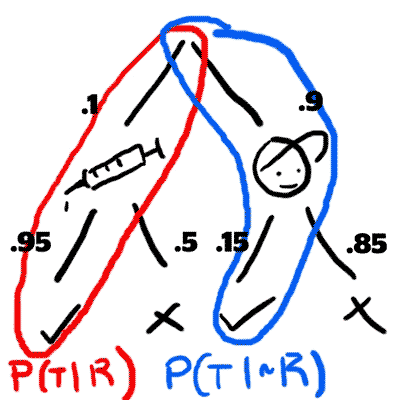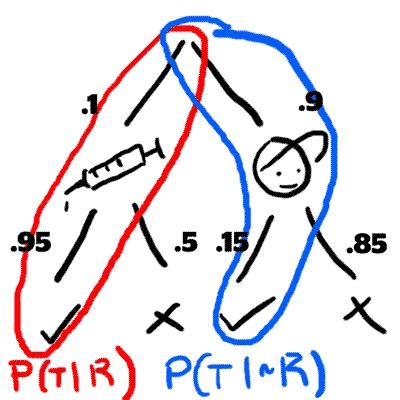
This information can be represented as a tree:

First, there is a 90% chance you will select a player who is clean

...and a 10% chance you will select a player on steroids

This is represented as follows:

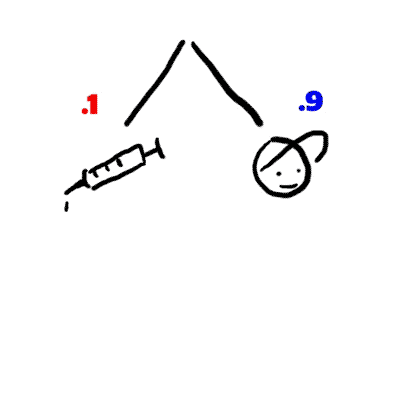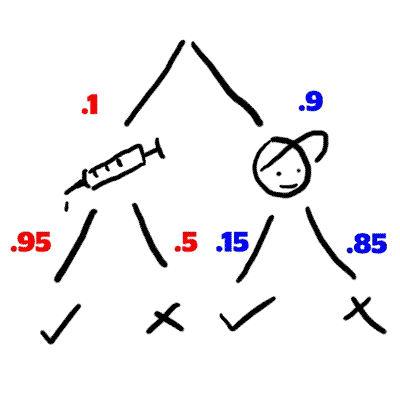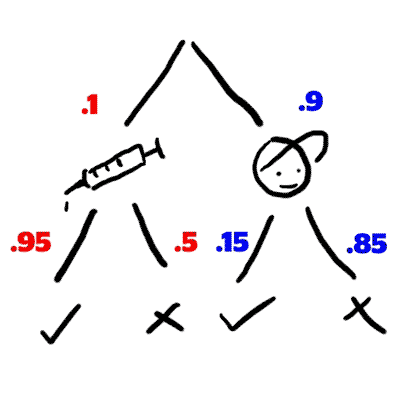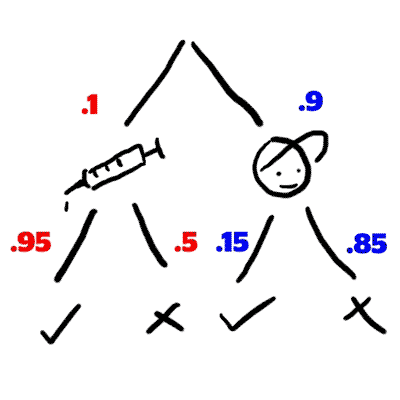
Then, there will be a 95% chance that the player on steroids will test positive, and a 15% chance that a player not on steroids will test positive.

Using principles from section 1, you can immediately see the conditional dependence.

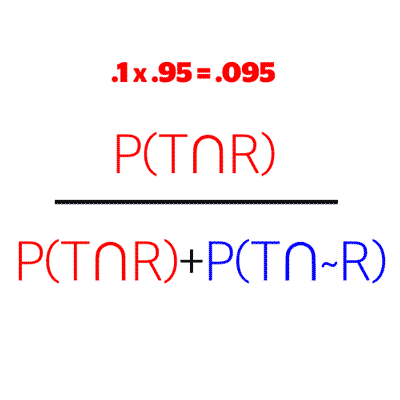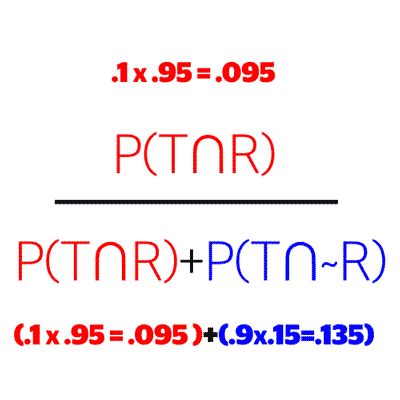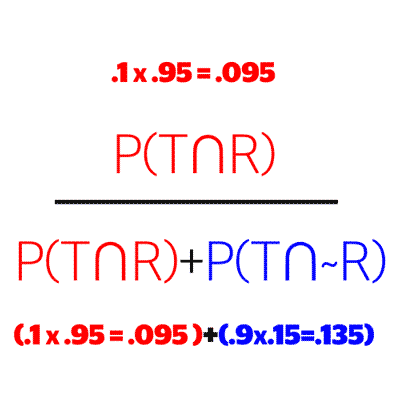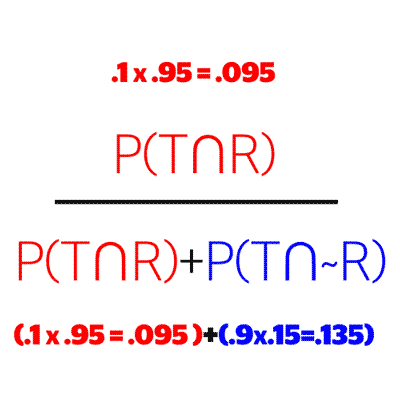
Step 3:

We know the probability of someone taking steroids and testing positive. That is the leftmost branch of our tree. This becomes the numerator.

Next we add the probability of getting a true positive and false positive together, and use the sum in our denominator. In other words, we are adding our two circled branches from step 2 together.

Finally, this evaluates to our answer.