Science:Math Exam Resources/Courses/MATH104/December 2013/Question 04/Solution 1

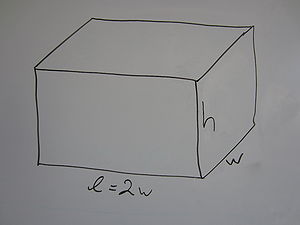
We wish to minimize the cost, C, subject to the constraint that the length of the base is twice it's width and that the volume of the container must be $V=8{\text{m}}^{3}$.

The cost C can be expressed as the sum of the costs for all the sides. Recall that this is an open-top box (i.e., no top). If we let l, w, and h denote the length, width, and height of the box in metres, respectively, then:

${\begin{aligned}C&=C_{\text{sides}}+C_{\text{bottom}}\\&=6(2hw+2hl)+4.5(lw)\end{aligned}}$

since material for the base costs $4.50 per square metre, and material for the sides costs $6 per square metre.

We are also given the constraint

$\displaystyle V=lwh=8$

Using the fact that the length is twice the width (i.e., l = 2w), the cost function and volume constraint are expressed as

$\displaystyle C=36hw+9w^{2},\quad V=2w^{2}h=8$

To reduce this into a single variable problem, we use the constraint to express the height of the box in terms of the width:

$h={\frac {4}{w^{2}}},$

and substitute this into the cost function C, making it a function of w only:

$C(w)={\frac {144}{w}}+9w^{2}$

To optimize C, we determine first determine its critical points by differentiating with respect to w and setting the derivative equal to zero:

${\begin{aligned}C'(w)&=-{\frac {144}{w^{2}}}+18w\\0&=-{\frac {144}{w^{2}}}+18w\\144&=18w^{3}\\8&=w^{3}\\w&=2\end{aligned}}$

Therefore w = 2 is a critical point. To determine whether or not it is the point that minimizes C, we use the second derivative test. The second derivative of C with respect to w is

$C''(w)={\frac {288}{w^{3}}}+18$

which is clearly greater than zero when w = 2. Thus, by the second derivative test, C has a local minimum at w = 2 (Moreover, it is the global minimum since there are no other critical points.) Substituting w = 2 into the cost function, we determine that the minimum cost is

$C(2)={\frac {144}{2}}+9(2)^{2}=72+36={\color {blue}\$108}$