Flight routes and linear programming 2
Introduction
General Problem: Resource allocation
The following problem exemplifies how linear programming, particularly the Revised Simplex Method, can be used to optimize resource allocation. By employing the following methodology, it is possible to find the least cost in order to move products across different locations along a finite set of routes, each having either a necessity for a product or a surplus of it. This methodology assumes the supply equals the demand, but there is no loss of generality if this was not the case (there would be minor adjustments done in that case). To carry out this methodology there must be a finite set of locations, identified as nodes from here on out. Additionally, we require a finite set of routes connecting them, where every route is one directional (two routes can be used to represent bidirectional routes).
Example Problem: Medicine Distribution
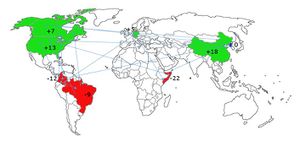
To illustrate this methodology we consider a global outbreak of a disease. Furthermore, we consider a finite set of countries with different requirement or surplus of medicine, each represented in the map below (a negative number represents a necessity for medicine). Assigning different costs to send medicine between these countries, and given there is more than one route by which the demand can be satisfied, this translates into a Linear Programming problem with the objective of finding the most efficient way to distribute the medicine in relation to cost.
Model
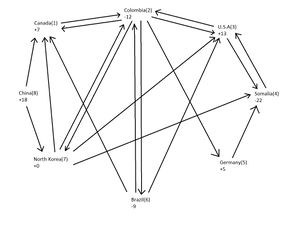
Our A matrix is also called a sink/source matrix. In other words, if a path is exiting a node, we label it as -1, and if a path is coming into a node, we label the path as 1 in our matrix. All countries start with some amount of resource, whether its 0, negative (deficit) or positive (surplus). Our eventual goal is to decide how much good to deliver in each path to minimize the cost of the project with a goal of allocation all resources evenly, so that all countries have a total surplus/deficit of 0. Thus, our b vector has values that are negative of how much a country starts with. For example, if China starts with +18 amount of resources, we expect its value in the b vector to be -18. In other words, china needs to lose 18 units of its resources in order to break even and get to a net surplus of 0.
By writing out our A and b in this way, we are indirectly restricting our x to be ≥ 0. In other words, since x represents the amount of good we ship in each path (one direction), it only makes logical sense for this to be non-negative, and our set-up forces it to be so.
A =
| -1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
| 1 | -1 | -1 | -1 | -1 | -1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | -1 | -1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | -1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | -1 | -1 | -1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | -1 | -1 | -1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | -1 |
c =
| 346 | 685 | 975 | 235 | 724 | 835 | 143 | 945 | 245 | 230 | 753 | 835 | 163 | 723 | 813 | 365 | 263 | 287 | 945 |
b =
| 7 | -12 | 13 | -22 | 5 | -9 | 0 | 18 |
Therefore, we can write this problem as follows: minimize cx such that Ax=b
By using "Matlab's Optimization Toolbox" we can solve for the vector x, representing the amount of goods transiting each route.
| X12 | X21 | X23 | X25 | X26 | X27 | X32 | X34 | X43 | X54 | X61 | X62 | X63 | X71 | X72 | X73 | X74 | X81 | X87 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 25 | 0 | 0 | 4 | 9 | 0 | 13 | 0 | 0 | 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 18 | 0 |
As mentioned, the analysis above was done by Matlab's Optimization Toolbox. In this toolbox, there exists a function linprog that solves a linear programming system for you. However, caution is needed when using this program and we ran into a couple of errors. First of all, linprog does the analysis by minimizing your objective function. This worked out for our case, since our goal was the minimize the total cost of shipment routes. Nevertheless, this was not the standard form that was taught in class, thus its always good to double check. Secondly, the function also omits the fact that all choice variables have to be greater or equal to zero (x≥0). We spent a lot of time troubleshooting this, because we kept getting answers like -10^21 ...etc. Thus, we had to manually bound our choice variables above zero. As long as all these points are noted, this toolbox is a great way to solve linear programming questions, and is very easy to use (inputs using matrices, specify which constraints are held with inequalities vs equalities).
Conclusion
Using a linear programming algorithm on Matlab we were able to determine the most efficient route for our problem and the results that we calculated are shown above.
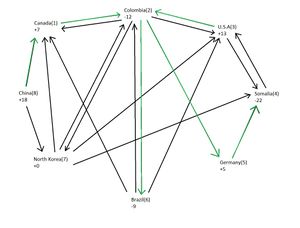
For the given problem the most efficient and cost effective route to distribute the medicine is shown on the table below and is highlighted in green.From this picture we can determine that the most efficient path for distributing medicine is to send all available medicine to Columbia and distributing the required number to the countries in need, with Somalia receiving its medicine through Germany. We did not consider the dual of our problem because we are dealing with our constraints being equalities (Ax = b) rather than inequalities which we have dealt with in class. Furthermore we did expect our results to be in integer form because all of our matrices A, b, and c are all of integer form. As explained in class, when your A,b, and c matrix/vectors are all integers, there is a very high chance that your solution will also be in integer form, as was the case for every problem seen in this class.