Course:MATH180/Archive/2011-2012/103/Examples

Limits

First, I'll say that Examples 2 & 3 pp.89-90 in the textbook are pretty good for explaining the intuitive idea of a limit.

Limits that Give a Number

Here is another example. Consider the function $f(x)={\frac {x^{2}-2x}{x^{2}-x-2}}$ and let us compute $\lim _{x\to 2}{\frac {x^{2}-2x}{x^{2}-x-2}}$. Since the numerator is 0 when x = 2, the function is not defined at that point (but it is defined for all values close to x = 2).

So, let us take some numbers approaching 2 and see what happens with the value of the function. We get the following table

x	f(x)
1	0.5
1.5	0.6
1.9	0.655
1.99	0.6656
1.999	0.6665

So, it seems that as x get closer and closer to 2, the value of the function f(x) gets closer and closer to 0.6666... = 2/3. Computing a limit means to be able to find this 2/3 without having to compute a list of values as we have just done it in the above table. And indeed, this limit is 2/3. We have $\lim _{x\to 2}{\frac {x^{2}-2x}{x^{2}-x-2}}=\lim _{x\to 2}{\frac {x(x-2)}{(x+1)(x-2)}}=\lim _{x\to 2}{\frac {x}{x+1}}$. The last function is defined at x = 2, hence we can just plug it in and we find $\lim _{x\to 2}{\frac {x^{2}-2x}{x^{2}-x-2}}=\dots =\lim _{x\to 2}{\frac {x}{x+1}}={\frac {2}{3}}$  !

Note that in the above table we are approximating the limit of $f(x)$ as x comes from the left (since we take values that are smaller than 2).

Limits that are Not Defined and Go to Infinity

Now let us look at $\lim _{x\to -1}{\frac {x^{2}-2x}{x^{2}-x-2}}$. Again, let us start by approximating the limit by using a list of values for x and f(x). We get

x	f(x)
-2	2
-1.5	3
-1.1	11
-1.01	101
-1.00001	100001

Table 1 : approximating the limit from the left-hand side.

What we see this time is that as x gets closer to -1 from the left, the value f(x) gets bigger and bigger (you can check by taking x closer and closer to -1). What should we conclude? that $\lim _{x\to -1}{\frac {x^{2}-2x}{x^{2}-x-2}}=\infty$ ??

Well, we know by the above computation that $\lim _{x\to -1}{\frac {x^{2}-2x}{x^{2}-x-2}}=\lim _{x\to -1}{\frac {x}{x+1}}$, and here we should be careful about the signs. Indeed, let us approximate the function from the right this time. We get

x	f(x)
0	0
-0.9	-9
-0.99	-99
-0.9999	-9999
-0.999999	-999999

Table 2 : approximating the limit from the right-hand side.

and so on. As x gets closer to -1, we see that the value of f(x) gets smaller and smaller, in other words, it goes toward $-\infty$.

To sum up, we have $\lim _{x\to -1^{-}}{\frac {x^{2}-2x}{x^{2}-x-2}}=\lim _{x\to -1^{-}}{\frac {x}{x+1}}=\infty$ and $\lim _{x\to -1^{+}}{\frac {x^{2}-2x}{x^{2}-x-2}}=\lim _{x\to -1^{+}}{\frac {x}{x+1}}=\infty$. In other words, x = -1 is a vertical asymptote!

Where does this phenomenon come from? who the hell invited him?

Let us have a look at the sign of ${\frac {x}{x+1}}$. If we take a number small than -1 (try with -2 for example), then both the numerator and denominator are negative. A negative number divided another negative number gives a positive number. Hence we get $+\infty$ when coming form the left.

Now, if we take a number bigger than -1 (try with -0.5 for instance), then the numerator is negative but the denominator is positive. Since a negative number divided by a positive number is negative, the whole fraction is negative. Hence we get $-\infty$ when coming form the right.

Note that in this second situation we have to take a number close enough to -1 (which the number we are interested in). Indeed, if we take a x = 0, then fraction is 0 as well. And if we take for x a number bigger than 0, then the fractions is negative. This is not a problem at all!! It only means that the function crosses the x-axis at x=0. That is indeed what we see in the graph of the function below.

Limits when x Goes to Infinity

Let us now check if the function has a horizontal asymptote. In order to do this, we have to compute the limit $\lim _{x\to \infty }f(x)=\lim _{x\to \infty }{\frac {x^{2}-2x}{x^{2}-x-2}}$. How do we do that? Since we have a fraction and we are looking at a limit when x goes to infinity, we have to look at the highest powers. Here the highest power of the numerator (top part) is $x^{2}$ and the highest power of the denominator (bottom part) is $x^{2}$ as well. Hence we are going to get a finite number. Indeed, we have $\lim _{x\to \infty }{\frac {x^{2}-2x}{x^{2}-x-2}}=\lim _{x\to \infty }{\frac {x^{2}(1-2/x)}{x^{2}(1-1/x-2/x^{2})}}=\lim _{x\to \infty }{\frac {1-2/x}{1-1/x-2/x^{2}}}$. When x becomes larger and larger the three expressions $-{\frac {2}{x}},~-{\frac {1}{x}}$ and $-{\frac {2}{x^{2}}}$ go to zero. Just to be sure, let us have a look at that for $-{\frac {1}{x}}$. We get the following table

x	-1/x
1	-1
10	-0.1
100	-0.01
1000	-0.001
1000000	-0.000001

So, indeed, $-{\frac {1}{x}}$ goes to 0 as x goes to infinity. It implies that for the limit $\lim _{x\to \infty }{\frac {1-2/x}{1-1/x-2/x^{2}}}$ as x goes to infinity we are left over with only ${\frac {1}{1}}=1$. This means that there is a horizontal asymptote whose equation is y = 1.

Since the limit when x goes to negative infinity is also 1 (if you are not convinced of that, simply notice that in table above if we replace 10 by -10 then we get +0.1 for -1/x), we have the same horizontal asymptote for the left-hand side of the graph.

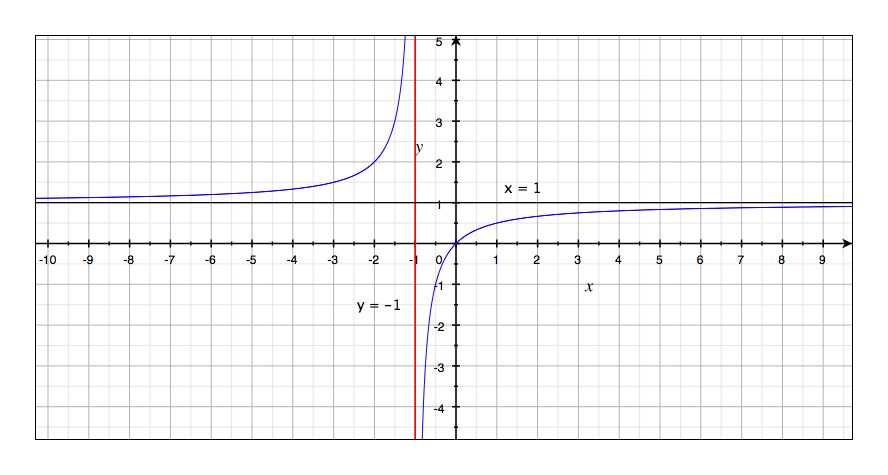
Indeed, the graph of the function is

In blue is the function $f(x)={\frac {x^{2}-2x}{x^{2}-x-2}}$, in red the vertical asymptote $x=-1$ and in black the horizontal asymptote $y=1$.

Note that Grapher (the software I've used to draw this graph) is not completely "honest" since the function is not defined for x = 2 and thus we should have a hole at x = 2. In fact, the program computes the limit so to say and actually draws the function $g(x)={\frac {x}{x+1}}$. This last function has exactly the same values as f(x) except at x = 2 where unlike f(x) it is defined and has the value of the limit, in other words (or rather symbols in this case...) we have $g(2)=\lim _{x\to 2}{\frac {x^{2}-2x}{x^{2}-x-2}}={\frac {2}{3}}$ whereas f(2) is undefined.

How Can we Know in Which of the above Cases we Are ?

Well, we can't. The only way is to determine between the first and the second case is... to actually compute the limit.

Left- vs Right-hand Limits

I had the impression in class that a few of you don't see the difference between right-hand and left-hand limit. Consider the limit $\lim _{x\to -1}{\frac {x^{2}-2x}{x^{2}-x-2}}=\lim _{x\to -1}{\frac {x}{x+1}}$ that we studied above.

To understand this idea of left-hand, right-hand limit, start by drawing a straight line on a piece of paper. The line represents the real numbers, negative infinity being on the very left and positive infinity being on the very right of your line. Now put -1 somewhere on the line (since we are studying the limit when x goes two -1).

We can approach -1 from two different sides. Either we take numbers that are smaller that -1 and then get closer to -1 (this what we do in Table 1). On your line we going toward -1 from the left. Hence the name, left-hand limit. If now we take values of x that are bigger (such as we do in Table 2), we then come from the right-hand side, hence the name right-hand limit.

Newton's Law of Cooling

Here is the correct version of the example (Exercise 16 p.243 in the textbook) I presented in class yesterday (Tuesday 18th October).

1. The data :

The room's temperature is 20°C, hence $T_{S}=20$,

at the start, the coffee has a temperature of 95°C, in other words, at time t=0 the temperature is 95°C, this translates as $T(0)=95$.

So far, plugging these pieces of information into the function $T(t)=T_{S}+(T(0)-T_{S})e^{kt}$ we have the function $T(t)=20+(95-20)e^{kt}=20+75e^{kt}$.

Now the question is how can we use that "when its temperature is 70°C, it is cooling at a rate of 1°C per minute"? (this is what I misread in while doing this example in class). In other words, what the "cooling rate" exactly is. The cooling rate is the rate at which the coffee's temperature is going down, or equivalently the rate of change of the coffee's temperature. The rate of change is nothing but the derivative !!! Hence this says that ${\frac {dT}{dt}}=-1$ when T(t) = 70.

Remember that the differential equation associated is ${\frac {dy}{dt}}=ky(t)$ with $y(t)=T(t)-T_{S}$. With the data above, T(t) = 70 gives y(t) = 70 - 20 = 50. Therefore, putting this into the above differential equation , we get $-1={\frac {dy}{dt}}=ky=k\cdot 50$. Thus, $-1=50k$ or $k=-1/50$.

Now keeping in mind that we have T(t) = 70, we can plug this k = -1/50 into our function and get $70=20+75e^{{\frac {-1}{50}}t}$. The rest of the question pretty straightforward, we simply have to find t. We get

${\begin{array}{rl}70=&20+75e^{{\frac {-1}{50}}t}\\50=&75e^{{\frac {-1}{50}}t}\\50/75=&e^{{\frac {-1}{50}}t}\\\ln(2/3)=&{\frac {-1}{50}}t\\\ln(2/3)\cdot {\frac {50}{-1}}=&t\\-50\ln(2/3)=&t.\end{array}}$

Just for the record, this is approximately 20.27 minutes.

Sorry for making a mistake about this example in class! If you have any question about it, don't hesitate to email me for further details.