Course:CPSC:Artificial Intelligence/States and Searching

This is a resource for members of the UBC community to create resources for learning about artificial intelligence.

To organize this resource, we will use the structure of Artificial Intelligence: Foundations of Computational Agents.

State Spaces

Place examples of how to represent problems in terms of state spaces here.

Applications of Search

Ricochet Robots

Game board

People occasionally get obsessed with algorithmic techniques (most of which are learned in a CS class). When trying to solve real-world problems using computers, however, we should not forget to draw upon experiences people accumulated from solving them manually. These experiences may provide new insights into the design of computational approaches. Using a popular board game, “Ricochet Robots”, as an example, Butko et al. discussed the complexity of solving it by different search algorithms. Everything below within this section is summarised from with some modification.

Rules

Ricochet Robots is played on a 16 × 16 grid of cells. A cell can be represented as (x,  y) where x denotes its horizontal position and y denotes its vertical position such that 0 ≤ x ≤ 15 (x ∈ ℕ) and 0 ≤ y ≤ 15 (y ∈ ℕ).

There are four robots, namely R₁,  R₂,  R₃ and R₄. Each robot occupies one cell, provided that each cell is occupied by at most one robot and no robot can occupy cells {(x,  y)∣x = 7  or 8,  y = 7  or 8}.

The border between two cells may have a barrier. Four cells in the middle are considered to be surrounded by barriers, i.e. a barrier is on the upper border and the left border of cell (7,  7), on the upper border and the right border of cell (8,  7), on the lower border and the left border of cell (7,  8), and on the lower border and the right border of cell (8,  8). Any robot can move horizontally or vertically over cells and it cannot stop until meeting an obstacle, i.e. another robot, a barrier or the border of the board. Exactly one robot can move each time.

Initially, a cell C is set as the goal position. Our task is to find the minimum number of steps such that robot R₁ reaches goal C. Robots R₂, R₃ and R₄ can also move to help robot R₁ reach goal C as fast as possible.

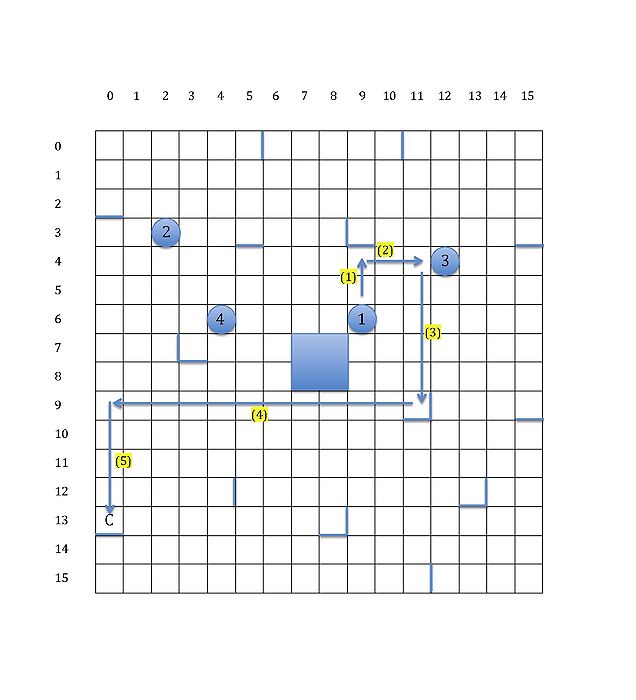
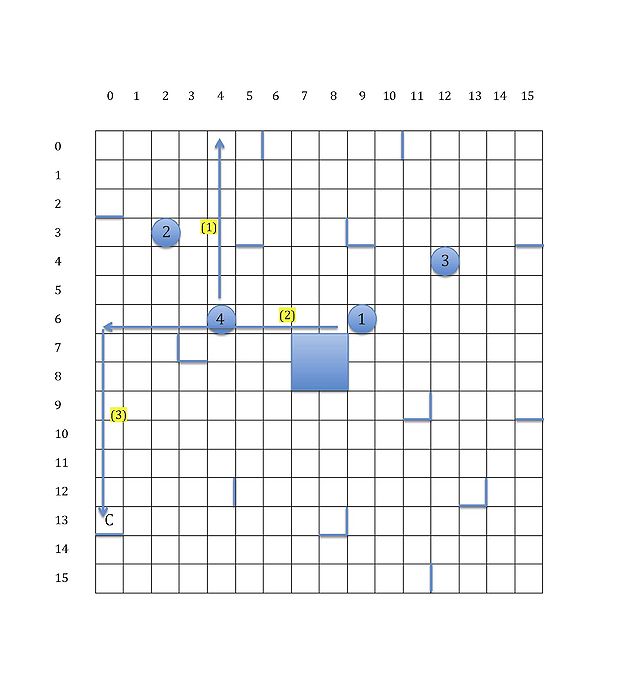
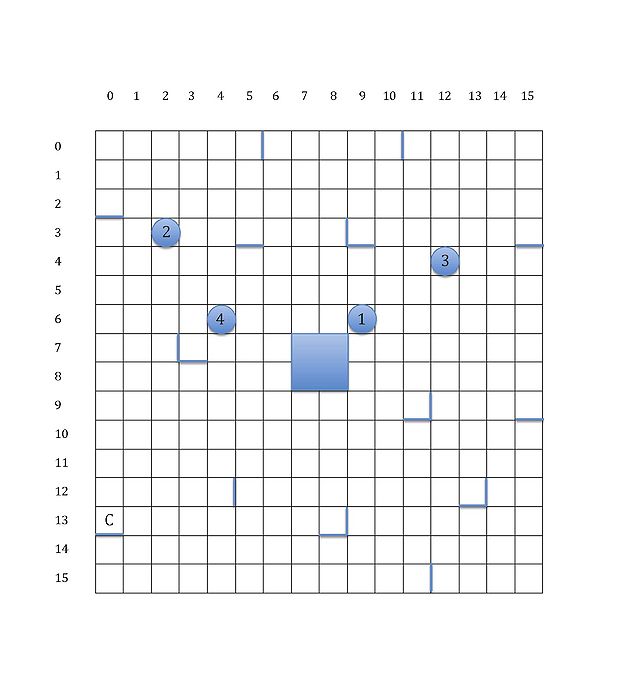
Here is an example showing two different strategies of moving robot R₁ to goal C. The first figure gives the board of Ricochet Robots. The second and third ones show two different strategies with or without moving Robot R₄. It turns out that the third one is an optimal solution. (There are two optimal solutions.)

Ricochet Robots game board (redrawn with modification based on )

First strategy of moving robot R₁ to goal C (redrawn with modification based on )

Second strategy of moving robot R₁ to goal C (redrawn with modification based on )

Search Problem

We formalise Ricochet Robots as a search problem. The first thing we should consider is its state space. Since our task is to let robot R₁ reach goal C after several moves of robots R₁,  R₂,  R₃ and R₄ under certain rules, the position of each robot should be contained in states. Thus a state can be represented by  < x₁,  y₁,  x₂,  y₂,  x₃,  y₃,  x₄,  y₄ >  which means robot R₁ is at (x₁,  y₁), robot R₂ is at (x₂,  y₂) and so forth. Given an example shown in the figure above, the initial state is  < 6,  9,  3,  2,  4,  12,  6,  4 >  and the goal state is  < 13,  0,  m,  n,  p,  q,  u,  v >  where the value of m,  n,  p,  q,  u and v may be different due to adopting different strategies.

A tree can be constructed accordingly where each vertex represents a state. The children of a vertex represent all possible states after one move of current state, and the root is the initial state. The level of a node is equal to the number of moves needed to transform from the initial state to current state. The figure below gives a tree built from our example. Initially, each of four robots can move in four directions, so there are 16 vertices linking from the root. In a general case, a robot stops besides an obstacle, which means it has at most three possible moves so that there are at most 12 possible moves in total. In the search tree, each vertex may have 12 children, so there are 12ⁿ vertices at level n. Although the branching factor may be smaller actually, the tree still grows exponentially.

Search tree of Ricochet Robots (redrawn with modification based on )

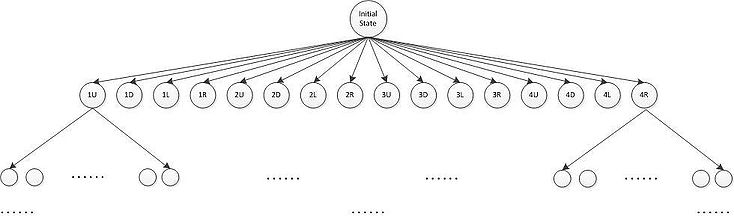
Given a search tree as discussed above, we want to find the vertex which represents the goal state at the lowest level. We should also notice that there may be vertices representing identical states at different levels. Next, we will try adopting different algorithms for searching trees.

Search Algorithms

Breadth First Search (BFS)

In breadth first search (BFS), we start from the root and visit nodes level by level. It is guaranteed that the optimal solution is found before any suboptimal solution, because the first goal state we find is the one with lowest level compared with other goal states. Despite of its efficiency in time, it is very costly in memory. Suppose we have visited all vertices at level l − 1, next we will analyze every possible move from level l − 1 to level l and store every vertex of level l in memory. With a branching factor b, the number of vertices stored in memory is b^l.

BFS with Path Pruning

With the help of path pruning strategies, the BFS algorithm can do better. We maintain all previous moves in memory and only visit states that have not been visited before, which means we no longer visit one state twice in a path. This strategy reduces the branching factor b with an additional cost of no more than double the size of memory. (This can be proved in a few steps.) The time of checking duplicates is proportional to the level instead of the total number of moves. Therefore, the performance can be improved with the cost of a little extra memory and extra time.

Depth First Search (DFS)

In depth first search (DFS), we visit a path until reaching a dead end, then we backtrack to the nearest next path, and so forth. Compared with BFS, we do not need to maintain every vertices of a level. What we need is to maintain current path only, which uses very little memory. However, it does not guarantee finding an optimal solution before finding suboptimal ones. What is even worse, it may not find a solution at all.

Depth Limited DFS (DLDFS)

Depth limited depth first search (DLDFS) works better. It performs DFS to vertices whose level is no more than the depth limit. The depth limit is set to 0 initially, and it increases from l to l + 1 after finishing searching all vertices whose level is no more than l. This search algorithm guarantees finding the optimal solution and finding it first.

However, the cost of memory is not ideal. When the depth limit is l, we have to perform DFS to vertices whose level is no more than l. Thus at this moment, vertices at level l − 1 have been visited twice, vertices at level l − 2 three times, ..., and the root l + 1 times. Although the redundancy seems awful, it is somewhat acceptable compared with the exponential growth of frontier at level l. In spite of using extra memory to reduce the branching factor in BFS, DLDFS has to use a naive branching factor. There is a tradeoff between time efficiency and memory efficiency.

A^* Search

A^* search is not a good option, either. Each move from a vertex to its child costs equally, so there is no way weighting different moves.

A Human Inspired Solver

Experienced Ricochet Robots players usually adopt two strategies in alternation. On the one hand, they try to solve the problem forwards. They are likely to consider where robot R₁ can be after four or five steps. On the other hand, they try to solve it backwards. Given goal C, they want to figure out from which positions robots can reach goal C in four or five steps.

These two strategies can also be mimicked by a computer. The first strategy can be mimicked easily, and the second one may involve recursive calls. Detailed discussion is omitted here due to space limit. People who are interested in this topic can visit for further reference.