Course:CPSC522/Titanic: Machine Learning from Disaster

Data Cleaning For "Titanic: Machine Learning from Disaster"

Author: Junyuan Zheng

Collaborators: Samprity Kashyap

Abstract

Figure 1: Just before midnight on April 14, 1912, the Titanic hit an iceberg on its maiden voyage.

Titanic: Machine Learning from Disaster is one of the competitions on Kaggle. You have to predict the fate of the passengers aboard the Titanic, which famously sank in the Atlantic Ocean during its maiden voyage from the UK to New York City after colliding with an iceberg.

One of the reasons that the shipwreck led to such loss of life was that there were not enough lifeboats for the passengers and crew. Although there was some element of luck involved in surviving the sinking, some groups of people were more likely to survive than others, such as women, children, and the upper-class.

However, this dataset has much missing value, most people in the competition are trying to use statistic method to fill the missing value. In this page, we will seek to achieve the same function by using neural network ensemble.

Builds on

Neural Network

Related Pages

Source Code can be found at GitHub

Content

Introduction

Titanic: Machine Learning from Disaster is one of the competitions on Kaggle. The participants have to predict the fate of the passengers aboard the Titanic, by using a dataset that is provided by Kaggle.

Kaggle provides two datasets:

1. a training set, which contains the outcome for a group of passengers as well as a collection of other parameters, such as their age, gender, etc.

2. a testing set, for which we have to predict the fate of each passenger based on a collection of attributes.

Figure 2: Original Dataset

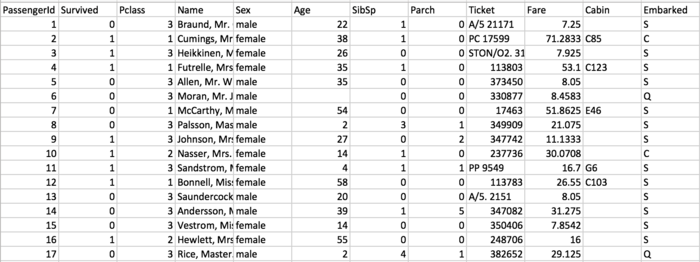
And here is a variable descriptions of the dataset.

survival	pclass	name	sex	age	sibsp	parch	ticket	fare	cabin	embarked
Survival	Passenger Class	Name	Sex	Age	Number of Siblings/Spouses Aboard	Number of Parents/Children Aboard	Ticket Number	Passenger Fare	Cabin	Port of Embarkation
0 = No; 1 = Yes	1 = 1st; 2 = 2nd; 3 = 3rd	N/A	N/A	N/A	N/A	N/A	N/A	N/A	N/A	C = Cherbourg; Q = Queenstown; S = Southampton

The datasets, offered by the Kaggle, contain 1310 individual's information. However, about 300 individual's age information are missing. Most people use two methods to solve the problem:

1. Delete all the rows that contain missing values, which means losing a lot of valuable information.

2. Use statistic method to fill those missing values.

Hypothesis: In this page, we will try to use neural network ensemble to fill missing age information

The rest of this study is organized as follows. The next section describes the Existing Techniques. In the Methodology section, we will introduce different models that are used in this project. In the Testing and Evaluation section, we will introduce the final result. We will also explain the Conclusion and Future Work.

Existing Techniques

Missing data can be a not so trivial problem when analyzing a dataset and accounting for it is usually not so straightforward either. Some quick fixes such as mean-substitution may be okay in some cases, but it will introduce bias into the data, for instance, applying mean substitution leaves the mean unchanged, which is desirable, but decreases variance, which may be undesirable.

The MICE package in R, helps you imputing missing values with plausible data values. These plausible values are drawn from a distribution specifically designed for each missing data point.

Here is a comparation of the MICE outputand the original data:

Figure 3: Comparing MICE Output with Original Data

We can see the distribution is almost the same. Therefore, it's reasonable to replace missing Age value from MICE output.

Methodology

Feature Engineering

Feature engineering is important in machine learning, sometimes a simple model with great features can outplay a complicated algorithm with poor one.

The fundamental idea behind feature engineering is transforming raw data into features that better represent the underlying problem, which will improve the model's accuracy on unseen data.

The reason that I use Feature Engineering in this project is, in the original dataset, we only have information about a person's Survival, Passenger Class, Name, Sex, Age, etc. Some of those information is not helpful to fill the missing age data, for instance, Ticket Number, Passenger Fare, Cabin, Port of Embarkation. To retrieve more information, I need to use feature engineering.

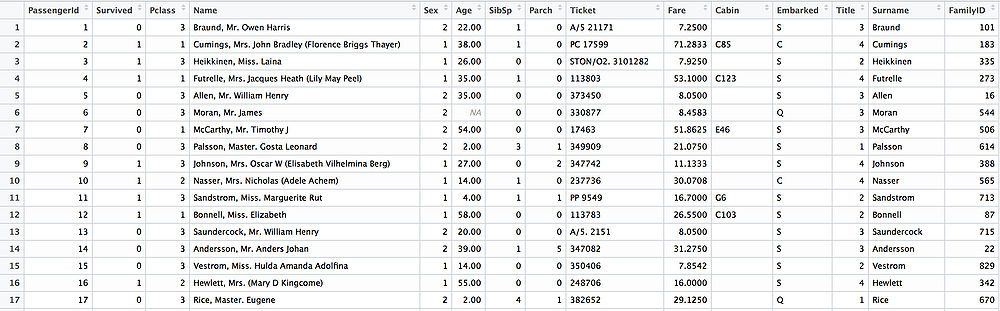
As a human being, if I want to guess one's age, I probably need to know his career, education background, salary, etc. But in this dataset, I do not have those information, but from Name, we can get Title information, from the Number of Siblings/Spouses Aboard, Number of Parents/Children Aboard we can generate Family Size. All of the derived information will be very helpful to guess the age information. For instance, if a person has a title Master, then we know he should be a boy or a young man, and that would be helpful to find his age information.

Finding Information from Passenger Name

If we scroll through the dataset, we can find a lot of different titles, including Miss, Mrs, Master. In order to extract these titles to make new variables, first, we need to use R to merge those training and testing dataset together.

After this step, the Title contains 5 variables.

Master	Miss	Mr	Mrs	Rare Title
61	264	757	198	29

Finding Family Information

The second information that I want to find is Family Information, the reason is straightforward. If I know the age distribution of a family, then this information would be helpful for me to speculate the age distribution of another family.

To achieve this, I will create a variable, which will be called FamilyID. All the people that have the same surname will be assigned to the same FamilyID.

Single Neural Network

In this part, we will use MATLAB to build a single feedforward neural network, and then using different training algorithm to train this neural network. The performance of the simple neural network will be compared by using RMSE and $R^{2}$ (coefficient of determination). The Root-Mean-Square Error (RMSE) is a frequently used measure of the differences between values predicted by a model or an estimator and the values actually observed. The Coefficient of Determination is a number that indicates how well data fit a statistical model – sometimes simply a line or a curve, and it is a key output of regression analysis.

Figure 4: A neural network model that will be used in this section

The input of the neural network will be the PClass, Sex, SibSp, Parch, Title and FamilyID, and the output is normalized Age.

In MATLAB, we can train this neural network by creating a net object, define hidden neural numbers and training algorithm.

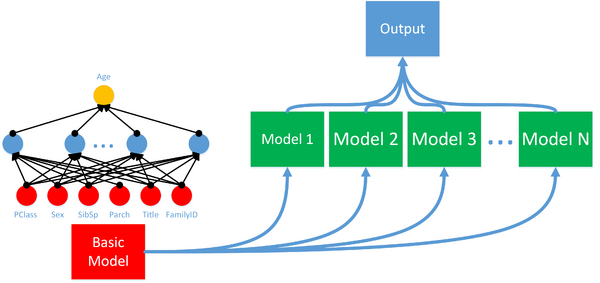
Neural Network Ensemble

To overcome the main limitations of ANN, for instance, generalization and overfitting, artificial neural network ensemble has been developed. Because of combining multiple neural networks learned from the same training samples, artificial neural network ensemble can remarkably enhance the forecasting ability and outperform any individual neural network. It is a practical approach to the development of a high-performance forecasting system.

In general, a neural network ensemble is constructed in two steps, i.e. training some component neural networks and then combining the component predictions.

A valuable property of neural networks is the generalization, which means a trained neural network can provide a correct matching in the form of output data for a set of previously unseen input data. For neural network ensemble, it needs to consist of diverse models with much disagreement, which will make it have a good generalization.

In this implementation, I plan to use three different methods:

1. Using different training algorithms, such as Gradient Descent with Momentum, Bayesian Regularization, and BFGS Quasi-Newton.

2. Using different initial weight, and hidden neuron number.

3. Training neural network with various data sets.

The original data set is partitioned into several different training subsets by using the random dividing method. Then these training sets are input to the different individual ANN models which will be executed concurrently. After training, each neural predictor has generated its result, and the neural network ensemble output will be the mean value of all the individual neural network output value.

Figure 5: Neural Network Ensemble

Further Investigation

In this section, we will focus on letting a single neural network learn the age pattern for people, who hold a Master title. The reason that we choose to use Master title is, as a human being, we can easily tell that a person with a Master title must be a young man, and combined with other information, we might be able to guess his age. By constraining the neural network input data set, we hope it will be easier for the single neural network to find the age distribution pattern.

The neural network building method is as same as the Single Neural Network. We use different training algorithm. The dataset contains 53 individuals with title Master.

Figure 6: Single Neural Network used in this section

Evaluations and Results

Feature Enginnering

Here is the dataset after the feature engineering.

Figure 7: Updated Dataset

We created two new attributes, Title and FamilyID. This dataset will be used in the next section.

Single Neural Network

The performance of the single neural network will be measured by using RMSE and $R^{2}$.

Here is a comparison of the results of different training algorithms:

Result\Method	Gradient Descent with Momentum	Bayesian Regularization	BFGS Quasi-Newton	Variable Learning Rate Gradient Descent
R2	0.3763	0.4877	0.3818	0.4013
RMSE	0.1425	0.1292	0.1419	0.1396

This table shows that the performance of the neural network is poor, the coefficient of determination is only 0.4. If we want to fill the missing age information, it is not wise to use the single neural network.

Neural Network Ensemble

As introduced before, the dataset is randomly divided into 10 subsets, and each subset contains 100 training data, therefore, we need ten individual neural network. The parameters that we used in this implementation are:

Parameter\Neural Network	No.1, 2	No. 3, 4	No.5, 6	No.7, 8	No.9, 10
Hidden Neuron	9, 12	8, 11	13, 7	15, 13	16, 15
Training Algorithm	Gradien Descent with Momentum	Bayesian Regularization	BFGS Quasi-Newton	Resilient Backpropagation	Levenberg-Marquardt

And here is the result:

Metrics	Result
R2	0.3606
RMSE	0.143467

As we can see, the performance of the ensemble method did worse than the single neural network method. However, if I use full data set to train every individual neural network, instead of dividing the data set into ten subsets. The performance is a little better comparing to the random dividing method, but without any improvement comparing to the simple neural network method.

Metrics	Result
R2	0.4496
RMSE	0.1339

Further Investigation

Here is the results for the Further Investigation section.

Result\Method	Levenberg-Marquardt	Bayesian Regularization	BFGS Quasi-Newton	Variable Learning Rate Gradient Descent
R2	0.2507	0	0	0
RMSE	0.0447	0.0520	0.0559	0.0615

From the result, we can see that the neural network cannot find a pattern and fit the data. We also build a neural network ensemble model, but the result is almost the same.

Here is a figure to show the difference between the expected result and actual neural network output.

Figure 8: Expected Output and Neural Network Output

This figure clearly demonstrates the problem of the neural network method. The issue is: as we can see, for the same expected output value, the neural network will generate different output values. For instance, for input A ([3 2 5 2 1]) and input B ([1 2 1 2 1]), the expected age is the same: 0.1357, but the output of the neural network is different, which means the neural network is not properly trained.

We also take a look at the data set, in which we find the reason why the neural network cannot be trained. If I check how many different inputs existed in the Master title dataset by running:

 unique(x, 'rows')

The return value shows only 17 individual inputs exist in the dataset, which means 2/3 inputs are duplicate. For those duplicate input, the output value is different. For instance, A can be represented by using 3rd Class, Male, two siblings on the ship, two parents on the ship, the title is master, and his age is ten years old. For B, he also has the same the parameters as A, but his age is eight years old. The same input but different output make the neural network cannot converge. Even if we use feature engineering to diminish the input data duplicate problem, it still exist and cannot be solved.

Here is a real example in the dataset:

Figure 9: Dataset Problem

As we can see in this dataset, the individual 1 and individual 2 have the same attributes, however, their age is different. Things are the same for individual 3 and individual 4. This is the main reason makes the neural network cannot converge.

Conclusion

In this page, I first introduce how to use the statistic method to fill the missing age value. Later, I test the hypothesis of using machine learning method to fill those missing value, explain and analysis the results.

All in all, comparing to statistic method, neural network is not suitable to fill the missing age in Titanic dataset, and here is a summary:

1. The Titanic dataset contains a lot of duplicates information. Even if we create more information by using feature engineering, about 1/3 neural network input data will still be the same, and because of the age information for those duplicate input is different. That's the main reason cause the neural network cannot converge. If we have more data about different people, then this method may be useful.

2. The probability method is better to solve the problem. It can analysis the age distribution of the original data set, to make sure after filling the missing data, the distribution will not change. However, the disadvantage might be: there filled age information may do not have a strong connection with other information.